Detailed description
Binary search is through the half method , Each time, the search scope is reduced to half of the original , If this halving can be achieved to a quarter or even more , It will be more efficient .
Interpolation search is such an algorithm , Similar to binary search , Interpolation lookup will start from The adaptive Start looking for , In essence, I will \(\frac1 2\) The search formula at position has been modified :
The detailed implementation steps of interpolation search are as follows :
- In an ordered list , Take the corresponding record as the comparison object through the proportion formula ;
- If the given value is equal to the keyword of the corresponding record , Then the search is successful ;
- If the given value is less than the keyword of the corresponding record , Then continue to search in the left half of the corresponding record ;
- If the given value is greater than the keyword of the corresponding record , Then continue to search in the right half of the middle record ;
- Keep repeating the process , Until the search is successful , Or all search areas have no records , Until the search fails .
Problem solving
Why is interpolation lookup \(\frac{key - a[low]}{a[high] - a[low]}\)?
For example , Look it up in an English Dictionary apple This word , I'm sure I won't start looking in the middle of the dictionary , Instead, start at the beginning of the dictionary , Because I think this way of finding is faster .
For an ordered sequence , If you can accurately predict the position of keywords in the sequence before searching , Such a search method can have better performance than binary search .
The difference formula \(\frac{key - a[low]}{a[high] - a[low]}\) Is to match the keyword to be searched with the largest in the sequence 、 Keyword comparison of the smallest record , Get a relatively more accurate location .
What are the precautions for using interpolation to find ?
For uniformly distributed sequences , The efficiency of interpolation search is very fast . Especially for absolutely uniformly distributed sequences ( The difference between adjacent elements is the same ), Interpolation search can be successful after only one comparison .
For sequences with very uneven distribution , The calculation of interpolation search will have the opposite effect , At this time, it's not as good as binary search .
Code implementation
Find interface
package cn.fatedeity.algorithm.search;
public interface Search {
int search(int[] numbers, int target);
}
Interpolation lookup class
package cn.fatedeity.algorithm.search;
/**
* Interpolation lookup class
*/
public class InterpolationSearch implements Search {
private int search(int[] numbers, int target, int left, int right) {
if (left > right) {
return -1;
} else if (left == right) {
if (numbers[left] == target) {
return left;
} else {
return -1;
}
}
if (target < numbers[left] || target > numbers[right]) {
return -1;
}
int scale = (target - numbers[left]) / (numbers[right] - numbers[left]);
int mid = left + (int) Math.floor(scale * (right - left));
if (numbers[mid] > target) {
return this.search(numbers, target, left, mid - 1);
} else if (numbers[mid] < target) {
return this.search(numbers, target, mid + 1, right);
} else {
return mid;
}
}
@Override
public int search(int[] numbers, int target) {
return this.search(numbers, target, 0, numbers.length - 1);
}
}



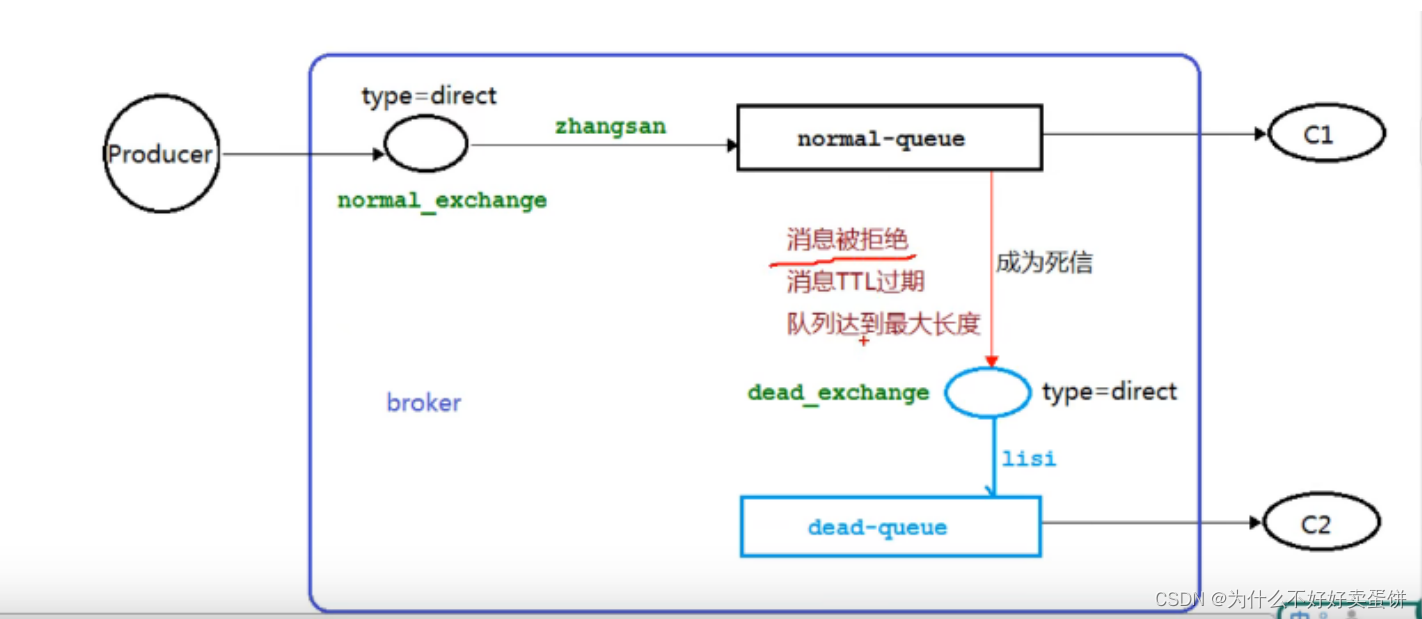

![[quick start of Digital IC Verification] 7. Basic knowledge of digital circuits necessary for verification positions (including common interview questions)](/img/90/aad9d7900d686efca10140717a5c5c.png)