当前位置:网站首页>【剑指Offer】6-10题
【剑指Offer】6-10题
2022-07-04 22:30:00 【你算哪一个bug?】
从尾到头打印链表
剑指 Offer 06. 从尾到头打印链表 - 力扣(LeetCode)
从尾到头,可以更改指向,但是比较麻烦,而且也改变了链表的结构。
观察打印的结构,是先打印尾再打印头的,和栈的结构很像,所以采用栈来写。
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
stack<int> st;
vector<int>ret;
ListNode* cur=head;
while(cur!=NULL)
{
st.push(cur->val);
cur=cur->next;
}
int sz=st.size();
ret.resize(sz);
for(int i=0;i<sz;i++)
{
ret[i]=st.top();
st.pop();
}
return ret;
}
};
重建二叉树
剑指 Offer 07. 重建二叉树 - 力扣(LeetCode)
构建树的思想:前序序列的第一个节点肯定是根节点,中序序列中根节点左边所有的节点都是左子树的,右边的都是右子树的,具体做法不再赘述。下面从代码实现的角度进行分析
这题的难点在于确定基准和确定递归函数的参数,区间其实都好算。
确定基准的意思是我用的元素的下标位置是以中序序列为基准还是以前序序列为基准。
下面我采用的是根节点的位置以前序序列为基准,所以递归函数参数中的pre_root就代表当前这棵树的根节点在前序序列中的位置,in_root和in_right表示的是这棵树在中序序列里的左右边界。
class Solution {
public:
//TreeNode* _bulidTree(TreeNode* root,int left,int right)//root如果不是int就不能确定根节点在前序遍历序列中的位置
TreeNode* _bulidTree(int pre_root,int in_left,int in_right)
{
if(in_left>in_right)//说明该结点对应的左右子树已经不合理
{
return NULL;
}
TreeNode* root=new TreeNode(preorder[pre_root]);//创建根节点
int x=find(inorder.begin(),inorder.end(),preorder[pre_root])-inorder.begin();//找到根节点在中序序列中的位置
int l_length=x-in_left;//左边区间的长度
int r_length=in_right-x;//右边区间的长度
root->left=_bulidTree(pre_root+1,in_left,in_left+l_length-1);//构建左子树
root->right=_bulidTree(pre_root+l_length+1,in_right-r_length+1,in_right);//构建右子树
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
this->preorder=preorder;//让子函数_buildTree里可以拿到preorder
this->inorder=inorder;//同理
TreeNode* root=_bulidTree(0,0,preorder.size()-1);//我的区间两边都是闭的
return root;
}
private:
vector<int> preorder;
vector<int> inorder;
};
这个代码还有一个可优化的点,仔细观察可以发现每次递归我都要计算根节点在中序序列中的位置,而find的底层是一个一个找过去的,效率不高,所以这里我们可以用哈希的思想把根节点在中序序列中的位置映射出来。
class Solution {
public:
//TreeNode* _bulidTree(TreeNode* root,int left,int right)//root如果不是整形就不能确定根节点在前序遍历序列中的位置
TreeNode* _bulidTree(int pre_root,int in_left,int in_right)
{
if(in_left>in_right)
{
return NULL;
}
TreeNode* root=new TreeNode(preorder[pre_root]);
// int x=find(inorder.begin(),inorder.end(),preorder[pre_root])-inorder.begin();
int l_length=dic[preorder[pre_root]]-in_left;//左边区间的长度
int r_length=in_right-dic[preorder[pre_root]];//右边区间的长度
root->left=_bulidTree(pre_root+1,in_left,in_left+l_length-1);
root->right=_bulidTree(pre_root+l_length+1,in_right-r_length+1,in_right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
this->preorder=preorder;
for(int i=0;i<inorder.size();i++)
{
dic[inorder[i]]=i;//映射中序序列元素的下标
}
TreeNode* root=_bulidTree(0,0,preorder.size()-1);
return root;
}
private:
vector<int> preorder;
vector<int> inorder;
unordered_map<int,int>dic;//字典,表示映射关系
};
二叉树的下一个结点
这题力扣没找到链接
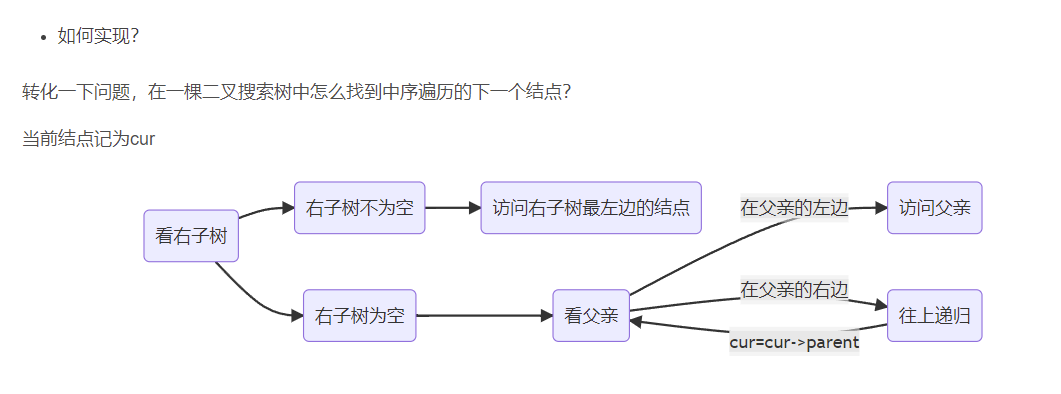
找出中序遍历的下一个结点
以前写红黑树的++时写过类似的,这里把当时的代码粘过来,详细的如下图(
这个图是我红黑树那篇博客里的内容)
self& operator++()//前置++
{
Node* cur = _node;
if (cur->_right)
{
//右子树不为空,不能直接把右子树的根给_node
//因为右子树最左边的叶子才是下一个应该访问的结点
Node* right = cur->_right;
while (right&&right->_left)
{
right = right->_left;
}
_node = right;
return *this;
}
else//右子树为空
//看父亲
{
Node* parent = cur->_parent;
while (parent&&parent->_right == cur)
{
cur = parent;
parent = cur->_parent;
}
if (parent == nullptr)
{
_node = nullptr;
}
else
{
_node = parent;
}
return *this;
}
}
用两个栈实现队列
剑指 Offer 09. 用两个栈实现队列 - 力扣(LeetCode)
用两个栈模拟队列的实现。
特别注意空栈情况,不处理空栈力扣编译都无法通过(VS跑的过)
class CQueue {
public:
CQueue() {}
void appendTail(int value) {
st1.push(value);
}
int deleteHead() {
if(st1.empty()&&st2.empty())//考虑两个都是空栈的情况,因为_ move并没有处理空栈
//如果两个传入的都是空栈,会导致stack为空时访问栈顶数据报错
{
return -1;
}
_move(st1,st2);
int x=st2.top();
st2.pop();
_move(st2,st1);
return x;
}
void _move(stack<int>&s1,stack<int>&s2)//把s1的数据移到s2里面
{
while(!s1.empty())
{
s2.push(s1.top());
s1.pop();
}
}
private:
stack<int>st1;
stack<int>st2;
};
斐波那契数列
剑指 Offer 10- I. 斐波那契数列 - 力扣(LeetCode)
根据题目给的公式递推即可。
class Solution {
public:
int fib(int n) {
if(n==0)
{
return 0;
}
else if(n==1)
{
return 1;
}
else
{
int pprev=0;//当前数字前一个的前一个
int prev=1;//当前数字的前一个
for(int i=2;i<=n;i++)
{
int tmp=(prev+pprev)%1000000007;
pprev=prev%1000000007;
prev=tmp;
}
return prev;//最后一次计算的结果由tmp给了prev
}
}
};
书上还给了一种logn的解法,但是写起来比较复杂,不够实用。
【扩展】青蛙跳台阶
剑指 Offer 10- II. 青蛙跳台阶问题 - 力扣(LeetCode)
斐波那契的变形,也可以用dp去做。
记青蛙跳上第n级阶梯的方案数为dp[n];则dp[n]=dp[n-1]+dp[n-2];比如青蛙在第N级阶梯,那它只能是从第N-1或者第N-2级上来的
class Solution {
public:
int numWays(int n) {
int a[]={
1,1};
if(n<2)
{
return a[n];
}
int ans=0;
int pprev=1;
int prev=1;
for(int i=2;i<=n;i++)
{
ans=(pprev+prev)%1000000007;
pprev=prev%1000000007;
prev=ans;
}
return ans;
}
};
【扩展】矩形覆盖
这题没找到链接…但也是斐波那契的变形。

边栏推荐
- Talk about Middleware
- 剑指Offer 68 - II. 二叉树的最近公共祖先
- Record: how to scroll screenshots of web pages on Microsoft edge in win10 system?
- Logo special training camp section II collocation relationship between words and graphics
- 共创软硬件协同生态:Graphcore IPU与百度飞桨的“联合提交”亮相MLPerf
- Shell script implements application service log warehousing MySQL
- 繁華落盡、物是人非:個人站長該何去何從
- Persistence mechanism of redis
- Logo Camp d'entraînement section 3 techniques créatives initiales
- 攻防世界 MISC 進階區 Erik-Baleog-and-Olaf
猜你喜欢

【OpenGL】笔记二十九、抗锯齿(MSAA)

攻防世界 misc 高手进阶区 a_good_idea
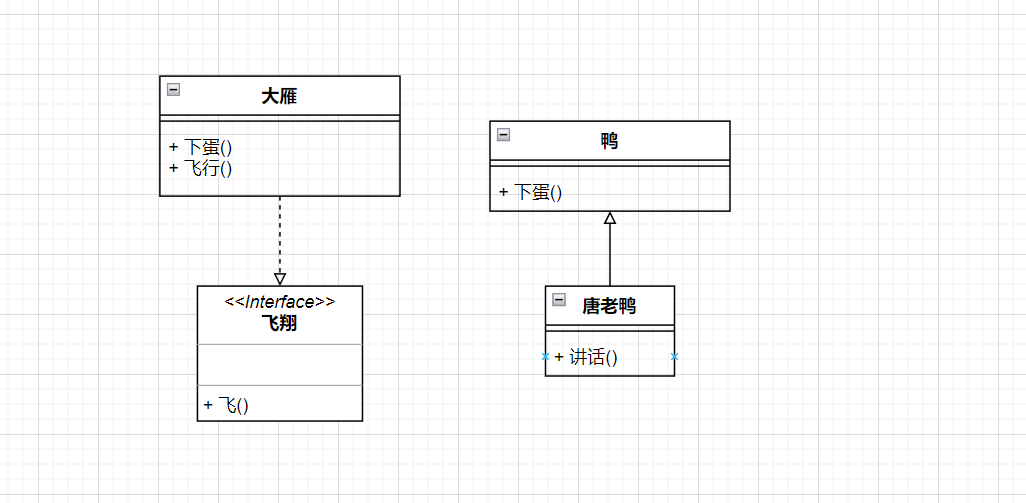
UML diagram memory skills
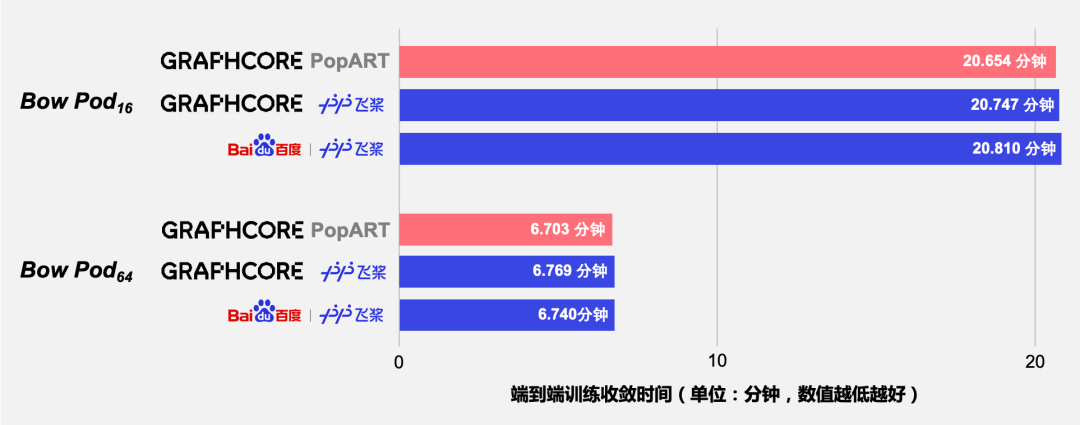
共创软硬件协同生态:Graphcore IPU与百度飞桨的“联合提交”亮相MLPerf
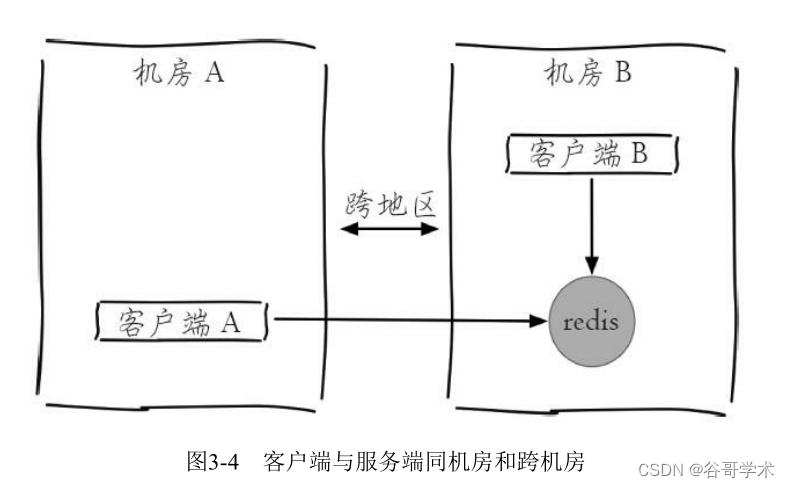
Redis入门完整教程:Redis Shell

LOGO特訓營 第一節 鑒別Logo與Logo設計思路
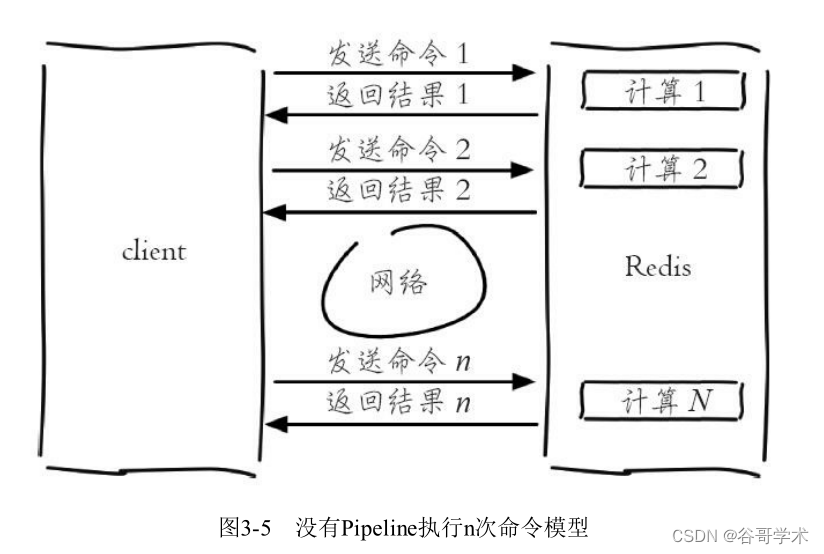
Redis入门完整教程:Pipeline
SPSS installation and activation tutorial (including network disk link)

Redis入门完整教程:慢查询分析

Attack and defense world misc advanced grace-50
随机推荐
攻防世界 MISC 高手进阶区 001 normal_png
Install the gold warehouse database of NPC
UML diagram memory skills
Create Ca and issue certificate through go language
Redis入门完整教程:发布订阅
攻防世界 MISC 进阶区 Ditf
LOGO特訓營 第一節 鑒別Logo與Logo設計思路
Solana chain application crema was shut down due to hacker attacks
Serial port data frame
Redis入门完整教程:Pipeline
Why is Dameng data called the "first share" of domestic databases?
华泰证券是国家认可的券商吗?开户安不安全?
Now MySQL cdc2.1 is parsing the datetime class with a value of 0000-00-00 00:00:00
啃下大骨头——排序(二)
Sword finger offer 68 - I. nearest common ancestor of binary search tree
Sword finger offer 68 - ii The nearest common ancestor of binary tree
Feature scaling normalization
Close system call analysis - Performance Optimization
安装人大金仓数据库
攻防世界 MISC 进阶区 3-11