当前位置:网站首页>Leetcode notes - dynamic planning -day7
Leetcode notes - dynamic planning -day7
2022-07-06 15:16:00 【LL. LEBRON】
List of articles
LeetCode Brush notes - Dynamic programming -day7
1014. The best combination of sightseeing
1. subject
Original link :1014. The best combination of sightseeing
2. Their thinking
- Observe carefully
a[i] + a[j] + i - j, Decomposable into :(a[j]-j)+(a[i]+i) - Again because
i<j, We canjAs current point , So we only need to traverse this problem . Use a variablefmaintainjAll before the dota[i]+iThe maximum of res=max(res,f+a[j]-j);The maximum value can be obtained by scanning once
3. Code
class Solution {
public:
int maxScoreSightseeingPair(vector<int>& a) {
int f=a[0];
int res=-1e9;
for(int i=1;i<a.size();i++){
res=max(res,f+a[i]-i);
f=max(a[i]+i,f);
}
return res;
}
};
121. The best time to buy and sell stocks
1. subject
Original link :121. The best time to buy and sell stocks

2. Their thinking
- Use a variable
minnmaintain[0,i-1] The minimum price of - Enumerate to
iwhen ,prices[i]-minnIt means the current pointiThe biggest gain from selling - Traverse all points , Taking the maximum :
res=max(res,prices[i]-minn);
3. Code
class Solution {
public:
int maxProfit(vector<int>& prices) {
int minn=1e9,res=0;
for(int i=0;i<prices.size();i++){
res=max(res,prices[i]-minn);
minn=min(minn,prices[i]);
}
return res;
}
};
122. The best time to buy and sell stocks II
1. subject
Original link :122. The best time to buy and sell stocks II
2. Their thinking
Algorithm : greedy
The specific situation can be divided into three categories :
- Single trading day : Set today's price P1、 Tomorrow's price P2, Then buy today 、 Exempt the earned amount tomorrow P2−P1( Negative values represent losses )
- Continuous rising trading day : Let the stock prices on this rising trading day be P1,P2,…,Pn Buy on the first day and sell on the last day , namely Pn−P1; Equivalent to buying and selling every day , namely Pn−P1=(P2−P1)+(P3−P2)+…+(Pn−Pn−1)
- Continuous decline in trading days : Then the trading income is the largest , That is, you won't lose money
Summary can be obtained : Since the number of transactions is not considered . Let's consider the stock price of the next two days , If the stock price of the next day is greater than that of the previous day , Then after the buy and sell operation , You can make a profit . Such greed will certainly make the greatest profit .
Directly traverse the entire array . If prices[i+1]-prices[i] Greater than 0, Then add the final total profit .
3. Code
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res=0;
for(int i=0;i<prices.size()-1;i++){
res+=max(0,prices[i+1]-prices[i]);
}
return res;
}
};

边栏推荐
- 软件测试方法有哪些?带你看点不一样的东西
- What level do 18K test engineers want? Take a look at the interview experience of a 26 year old test engineer
- Do you know the performance testing terms to be asked in the software testing interview?
- [pytorch] simple use of interpolate
- Interview answering skills for software testing
- How to write the bug report of software test?
- Emqtt distribution cluster and node bridge construction
- How to learn automated testing in 2022? This article tells you
- Global and Chinese markets for GaN on diamond semiconductor substrates 2022-2028: Research Report on technology, participants, trends, market size and share
- Global and Chinese market of RF shielding room 2022-2028: Research Report on technology, participants, trends, market size and share
猜你喜欢
ucore lab7 同步互斥 实验报告
ucore lab8 文件系统 实验报告
The salary of testers is polarized. How to become an automated test with a monthly salary of 20K?
Report on the double computer experiment of scoring system based on 485 bus
What are the software testing methods? Show you something different

How to transform functional testing into automated testing?

Interface test interview questions and reference answers, easy to grasp the interviewer
Example 071 simulates a vending machine, designs a program of the vending machine, runs the program, prompts the user, enters the options to be selected, and prompts the selected content after the use
What is "test paper test" in software testing requirements analysis
What level do 18K test engineers want? Take a look at the interview experience of a 26 year old test engineer
随机推荐
How to rename multiple folders and add unified new content to folder names
Global and Chinese market of pinhole glossmeter 2022-2028: Research Report on technology, participants, trends, market size and share
ArrayList集合
What if software testing is too busy to study?
安全测试入门介绍
Servlet
Réponses aux devoirs du csapp 7 8 9
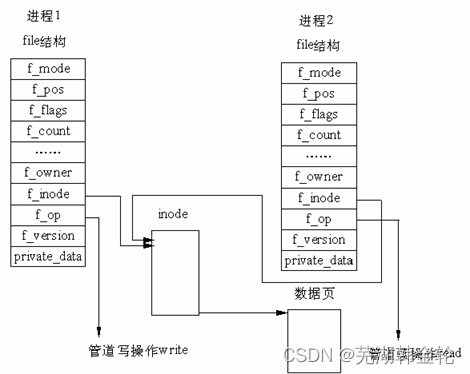
Differences between select, poll and epoll in i/o multiplexing
What are the software testing methods? Show you something different
Interface test interview questions and reference answers, easy to grasp the interviewer
How to learn automated testing in 2022? This article tells you
The minimum number of operations to convert strings in leetcode simple problem
Leetcode simple question: check whether two strings are almost equal
MySQL transactions
Emqtt distribution cluster and node bridge construction
ucore lab6 调度器 实验报告
Global and Chinese markets for GaN on diamond semiconductor substrates 2022-2028: Research Report on technology, participants, trends, market size and share
Investment should be calm
The most detailed postman interface test tutorial in the whole network. An article meets your needs
Pedestrian re identification (Reid) - Overview

