当前位置:网站首页>树——前序
树——前序
2022-08-03 05:25:00 【JanNinth】
树的总结:
- 概念(前序)
- 树的作用
- 二叉树
- 完全二叉树
- 代码(golang)——实现树结构基本定义
- 二叉排序树(二叉查找/搜索树)
- 平衡二叉树AVL
- 红黑树
- 线索二叉树(了解)
- 赫夫曼树
- B树(数据库)
- B+树(索引)
- 最小生成树
概念:
1、为什么存在树结构
相比于数组与链表:
数组的查询速度快O(1),但是删除等操作慢O(n)
链表的删除插入等操作快O(1),但是查询速度慢O(n)
树结构在一定程度上起到综合作用
查询时间复杂度(平均):O(logn)
删除插入操作(不同树结构不同)
2、二叉树
数据结构一般树结构,一般指 二叉树
根节点:头结点,树最上面的节点
父节点、子节点:如果一个节点下面连接多个节点,那么该节点称为父节点,它下面的节点称为子 节点。
叶子节点:没有任何子节点的节点称为叶子节点。
兄弟节点:具有相同父节点的节点互称为兄弟节点。
树的深度:从根节点开始(其深度为0)自顶向下逐层累加的。上图中,13的深度是1,30的深度是2,28的深度是3。
树的高度:从叶子节点开始(其高度为0)自底向上逐层累加的。54的高度是2,根节点23的高度是3
3、完全二叉树
二叉树的所有叶子结点都在最后一层或者倒数第二层,而且最后一层的叶子结点在左边连续,倒数第二层的叶子结点在右边连续,我们称之为全完二叉树。
4、代码实现树
二叉树 可以使用链表构成也可以使用数据:此处使用链表
// 定义二叉树结构
type LinkNode struct {
val int //二叉树存储的数据
leftNode *LinkNode //左节点
RightNode *LinkNode //右结点
}边栏推荐
- 自监督论文阅读笔记FIAD net: a Fast SAR ship detection network based on feature integration attention and self
- 关于芯片你了解吗?
- 6. What is the difference between Vector, ArrayList and LinkedList?(design, performance, safety)
- ZEMAX | 如何使用渐晕系数
- 三、final、finally、 finalize有什么不同?
- ZEMAX | 探索 OpticStudio中的序列模式
- MATLAB给多组条形图添加误差棒
- MySql【后面附有练习题】
- 二分查找6 - 寻找峰值
- Delightful Nuxt3 Tutorial (2): Build a Blog Quickly and Easily
猜你喜欢

二分查找5 - 第一个错误的版本
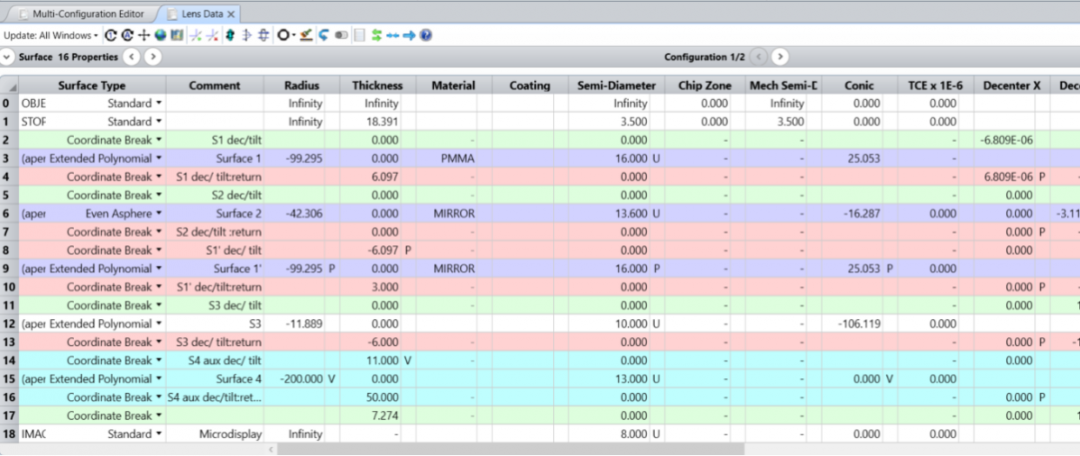
ZEMAX | 在OpticStudio中建立扩增实境(VR)头戴式显示器
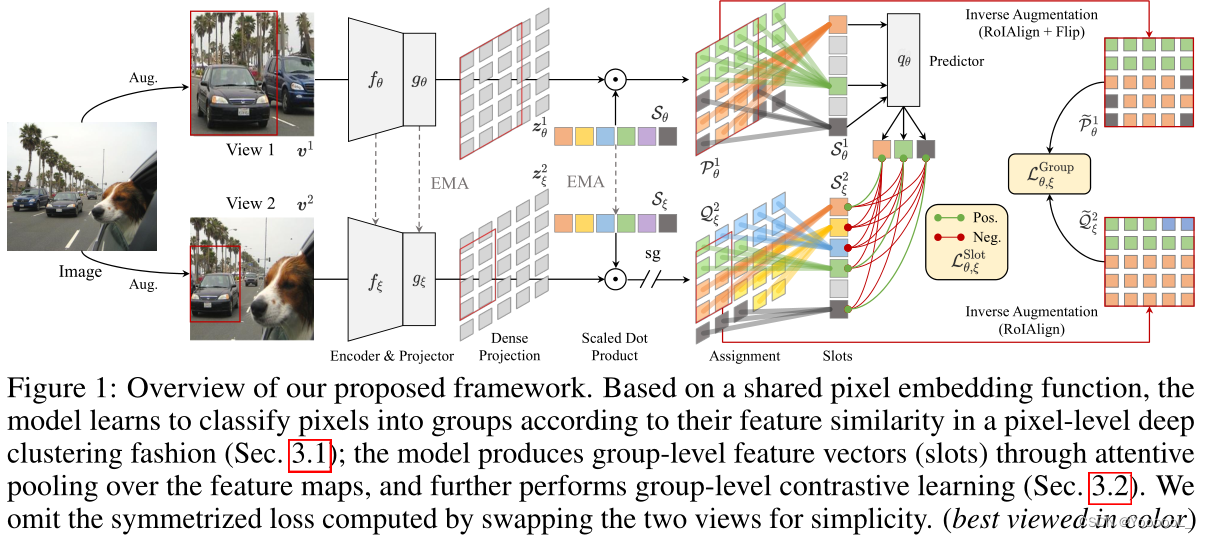
自监督论文阅读笔记 Self-Supervised Visual Representation Learning with Semantic Grouping
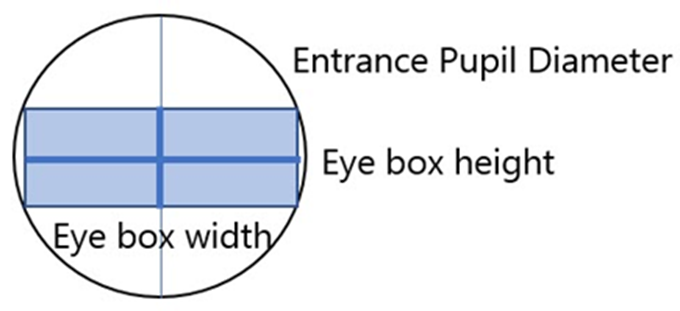
ZEMAX | 在设计抬头显示器(HUD)时需要使用哪些工具?
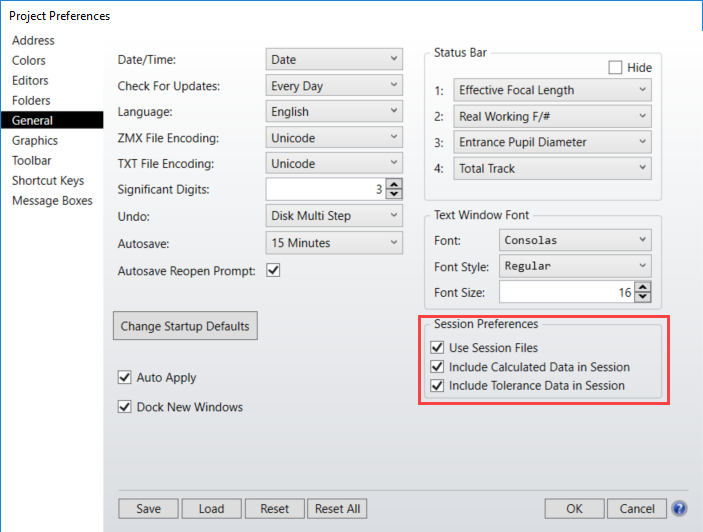
ZEMAX | 探索 OpticStudio中的序列模式
使用JSP实现简单的登录注册功能,并且使用Session跟踪用户登录信息

稳压二极管的工作原理及稳压二极管使用电路图

pandoc -crossref插件实现markdwon文档转word后公式编号自定义
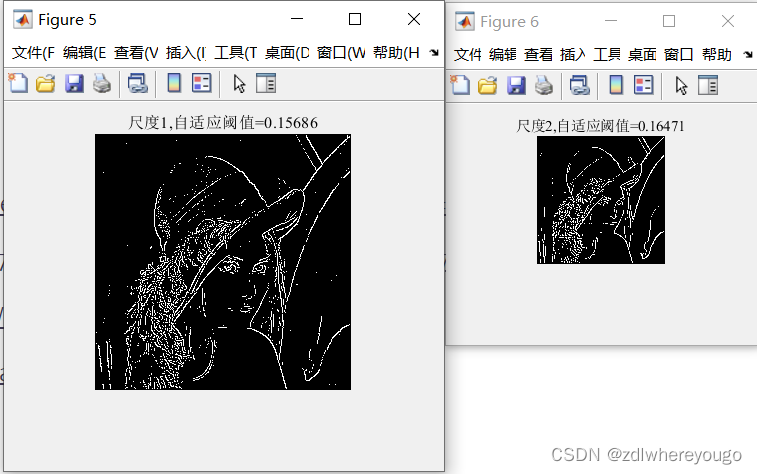
MATLAB自带的dwt2和wavedec2函数实现基于小波变换的自适应阈值图像边缘检测
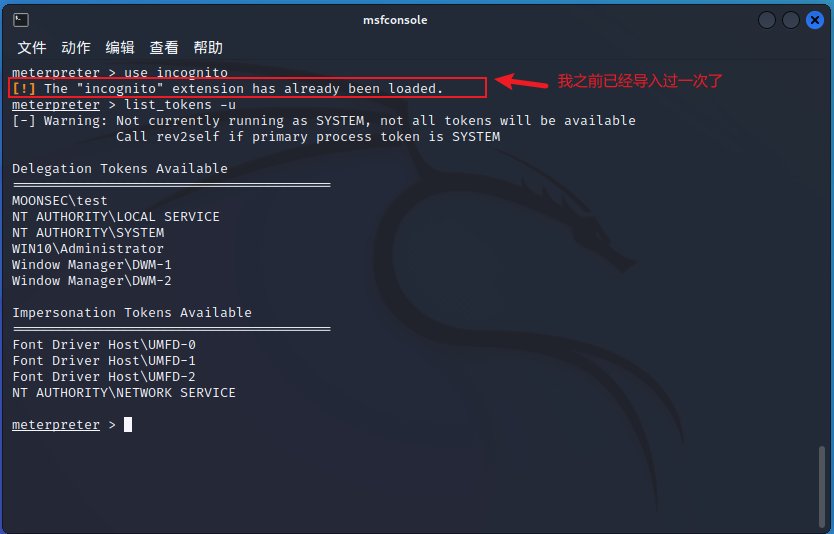
Windos 内网渗透之Token的使用
随机推荐
芯片解密工作应该具备哪些条件?唯样商城
g++参数说明
JS--正则表达式
自监督论文阅读笔记 SimCLRV2 Big Self-Supervised Models are Strong Semi-Supervised Learners
深度学习理论课程第四、五章总结
001_旭日X3派初探:开箱测试
KASLR-内核地址空间布局随机化
进程间通信IPC - 信号量
快速的将结构体各成员清零
【第三周】ResNet+ResNeXt
2021-04-23
SolidWorks 操作视频 | 隐藏高手必备工具Defeature,让设计隐藏更彻底
VSCODE 常见问题
【第二周】卷积神经网络
A.1#【内存管理】——1.1.4 node: 初始化
MCU接收串口字符型数据转换成数据型数据
ZEMAX | 绘图分辨率结果对光线追迹的影响
IPC通信 - 管道
ZEMAX | 如何创建复杂的非序列物体
六、对比Vector、ArrayList、LinkedList有何区别?(设计、性能、安全)