当前位置:网站首页>Poj1821 fence problem solving Report
Poj1821 fence problem solving Report
2022-07-07 10:58:00 【Aurora_ yxy】
1 Title Description
A team of $k (1 <= K <= 100) $workers should paint a fence which contains N ( 1 < = N < = 16000 ) N (1 <= N <= 16 000) N(1<=N<=16000) planks numbered from 1 1 1 to N N N from left to right. Each worker i ( 1 < = i < = K ) i (1 <= i <= K) i(1<=i<=K) should sit in front of the plank S i S_i Si and he may paint only a compact interval (this means that the planks from the interval should be consecutive). This interval should contain the Si plank. Also a worker should not paint more than Li planks and for each painted plank he should receive P i ( 1 < = P i < = 10000 ) P_i (1 <= P_i <= 10 000) Pi(1<=Pi<=10000). A plank should be painted by no more than one worker. All the numbers Si should be distinct.
Being the team’s leader you want to determine for each worker the interval that he should paint, knowing that the total income should be maximal. The total income represents the sum of the workers personal income.
Write a program that determines the total maximal income obtained by the K workers.
Yes N N N The planks line up from left to right , Yes K K K A craftsman painted the boards , Each board shall be painted at most once . The first i i i A craftsman either doesn't paint , Either the whitewash contains wood i i i Of , Length not exceeding L i L_i Li A continuous piece of wood , Each piece of painted wood can get $P_i $ The reward for .
Ask how to arrange to make the craftsmen get the maximum total remuneration .
Input
The input contains:
Input
N K
L1 P1 S1
L2 P2 S2
…
LK PK SK
Semnification
N -the number of the planks; K ? the number of the workers
Li -the maximal number of planks that can be painted by worker i
Pi -the sum received by worker i for a painted plank
Si -the plank in front of which sits the worker i
Output
The output contains a single integer, the total maximal income.
Examples
The sample input 1
8 4
3 2 2
3 2 3
3 3 5
1 1 7
Sample output 1
17
Tips
Explanation of the sample:
the worker 1 paints the interval [1, 2];
the worker 2 paints the interval [3, 4];
the worker 3 paints the interval [5, 7];
the worker 4 does not paint any plank
2 Ideas
2.1 Violence without optimization
First of all, all the craftsmen should follow Si Sort from small to large
• state :f[i][j], front i A craftsman before painting j A board ( Allow null ) The maximum reward for .
• State transition equation :
The first i i i A craftsman does nothing : f [ i ] [ j ] = f [ i − 1 ] [ j ] f[i][j]=f[i-1][j] f[i][j]=f[i−1][j]
The first j j j A piece of wood can be left empty without painting : f [ i ] [ j ] = f [ i ] [ j − 1 ] f[i][j]=f[i][j-1] f[i][j]=f[i][j−1]
Consider the $ i $ A craftsman painted the first k + 1 j k+1~j k+1 j block ,
𝑓[𝑖][𝑗] =𝑚𝑎𝑥{𝑓[𝑖 − 1][𝑘] + 𝑃𝑖 ∗ (𝑗 − 𝑘)}, among 𝑗−𝐿𝑖≤𝑘≤𝑆𝑖−1,𝑗 ≥ 𝑆𝑖
enumeration i i i, j j j, k k k, The time complexity is O ( n 2 k ) O(n^2k) O(n2k)
Because we can see that the data is not so small : 1 < = K < = 100 1 <= K <= 100 1<=K<=100, 1 < = N < = 16000 1 <= N <= 16 000 1<=N<=16000
Obviously not
So , We consider optimizing with priority queues
2.2 Priority queue optimization dp
Optimize :𝑓[𝑖][𝑗] =𝑚𝑎𝑥{𝑓[𝑖 − 1][𝑘] + 𝑃𝑖 ∗ (𝑗 − 𝑘)}, among 𝑗 ≥ 𝑆𝑖,𝑗−𝐿𝑖≤𝑘≤𝑆𝑖−1
• Loop the outermost layer i Regarded as fixed value , Consider inner circulation j And decision making k , Convert to get :
• 𝑓[𝑖][𝑗] = 𝑃𝑖 ∗ 𝑗 +𝑚𝑎𝑥{𝑓[𝑖 − 1][𝑘] − 𝑃𝑖 ∗ 𝑘)}, among 𝑗−𝐿𝑖≤𝑘≤𝑆𝑖−1,𝑗 ≥ 𝑆𝑖
Maintain a decision point k Monotone increasing , The number f [ i − 1 ] [ k ] − P i × k f[i-1][k]-Pi×k f[i−1][k]−Pi×k Monotonic decline Queues ,
Only the decision in this queue can be the best decision at a certain moment
• Monotonic queue support :
When j When it gets bigger , Inspection team leader , Will be less than j-Li Out of the team .
When querying the optimal decision , The team leader is the maximum value
When new decisions join the team , Check the tail of the team f [ i − 1 ] [ k ] − P i × k f[i-1][k]-Pi×k f[i−1][k]−Pi×k The monotonicity of , Useless decisions come out of the team , new
Make a decision to join the team
2 Concrete realization
- For each outer loop i,
When the inner loop starts ( j = S i j=S_i j=Si), Create an empty monotone queue ,
The interval [ m a x ( j − L i , 0 ) , S i − 1 ] [max(j-Li,0),Si-1] [max(j−Li,0),Si−1] The decision is added to the monotone queue , perform 3
- For each of these j = S i N j=Si~N j=Si N,
First, check whether the team leader is legal (1), Then take the team leader as the optimal strategy ( operation 2) Make a state transition , Then join the team (3)
The total time complexity is zero O(NK)
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+2,K=1e2+2;
struct node{
int l,s,p;
}a[K];
bool cmp(node x,node y){
return x.s<y.s;
}
int f[K][N],q[N],n,k;
int main(){
while(~scanf("%d%d",&n,&k)){
for(int i=1;i<=k;i++) {
scanf("%d%d%d",&a[i].l,&a[i].p,&a[i].s);
}
sort(a+1,a+k+1,cmp);
memset(f,0,sizeof(f));
for(int i=1;i<=k;i++){
int hd=0,tl=0;
q[tl++]=max(0,a[i].s-a[i].l);
for(int j=1;j<=n;j++){
f[i][j]=max(f[i-1][j],f[i][j-1]);
if(j>=a[i].s+a[i].l) continue;
while(hd<tl&&q[hd]+a[i].l<j) hd++;
if(j>=a[i].s) f[i][j]=max(f[i][j],f[i-1][q[hd]]+a[i].p*(j-q[hd]));
else{
int x=f[i-1][j]-j*a[i].p;
while(hd<tl&&f[i-1][q[tl-1]]-q[tl-1]*a[i].p<x) tl--;
q[tl++]=j;
}
}
}
printf("%d\n",f[k][n]);
}
return 0;
}
End of the flower *
·*,°*:.*( ̄▽ ̄)/$:.°* .
边栏推荐
- How much review time does it usually take to take the intermediate soft exam?
- 單調性約束與反單調性約束的區別 monotonicity and anti-monotonicity constraint
- 2022年7月10日“五心公益”活动通知+报名入口(二维码)
- VR development optimization
- Deeply analyze the main contents of erc-4907 agreement and think about the significance of this agreement to NFT market liquidity!
- I plan to take part in security work. How about information security engineers and how to prepare for the soft exam?
- Use load_ decathlon_ Datalist (Monai) fast loading JSON data
- 2021 summary and 2022 outlook
- 深入理解Apache Hudi异步索引机制
- 【STM32】实战3.1—用STM32与TB6600驱动器驱动42步进电机(一)
猜你喜欢
使用Tansformer分割三维腹部多器官--UNETR实战
What are the contents of the intermediate soft test, the software designer test, and the test outline?
ADB utility commands (network package, log, tuning related)
2022年上半年5月网络工程师试题及答案
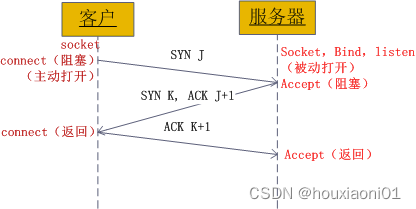
Socket communication principle and Practice
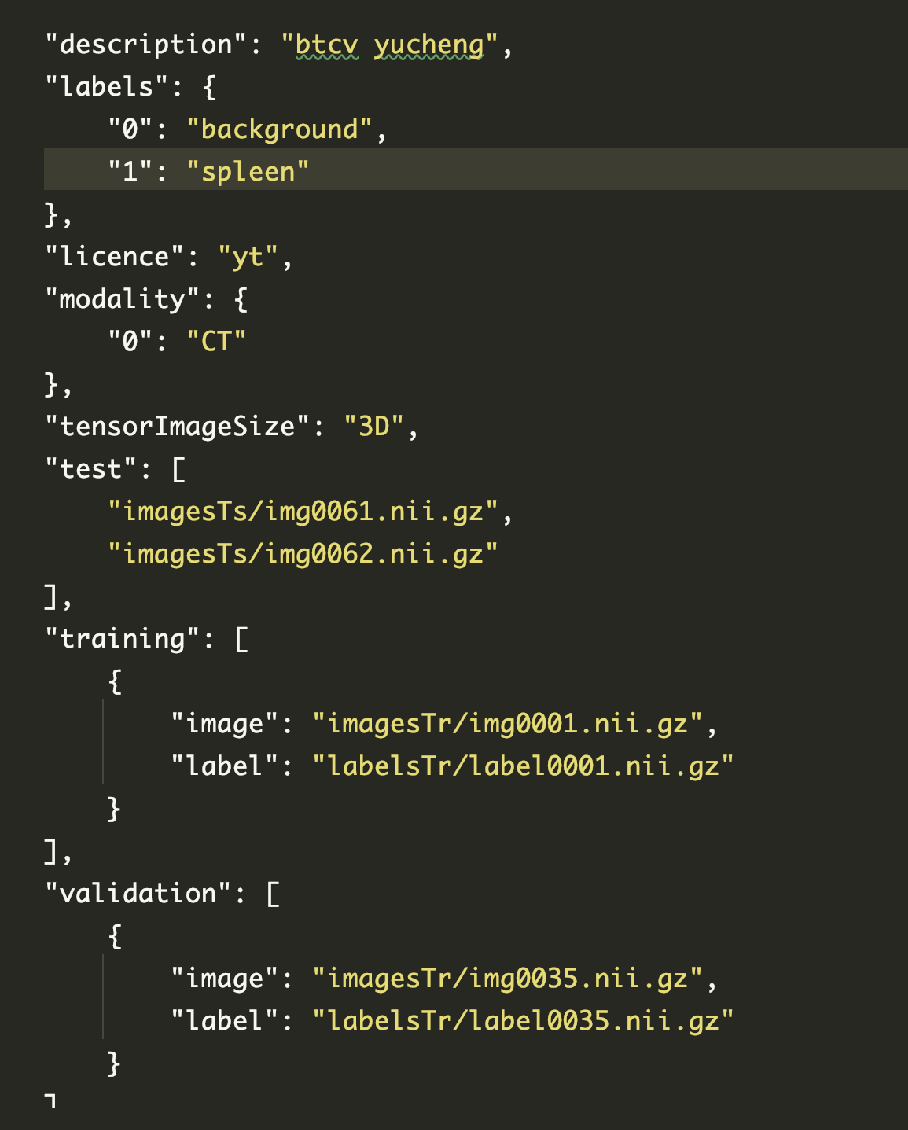
使用 load_decathlon_datalist (MONAI)快速加载JSON数据

Idea shortcut keys
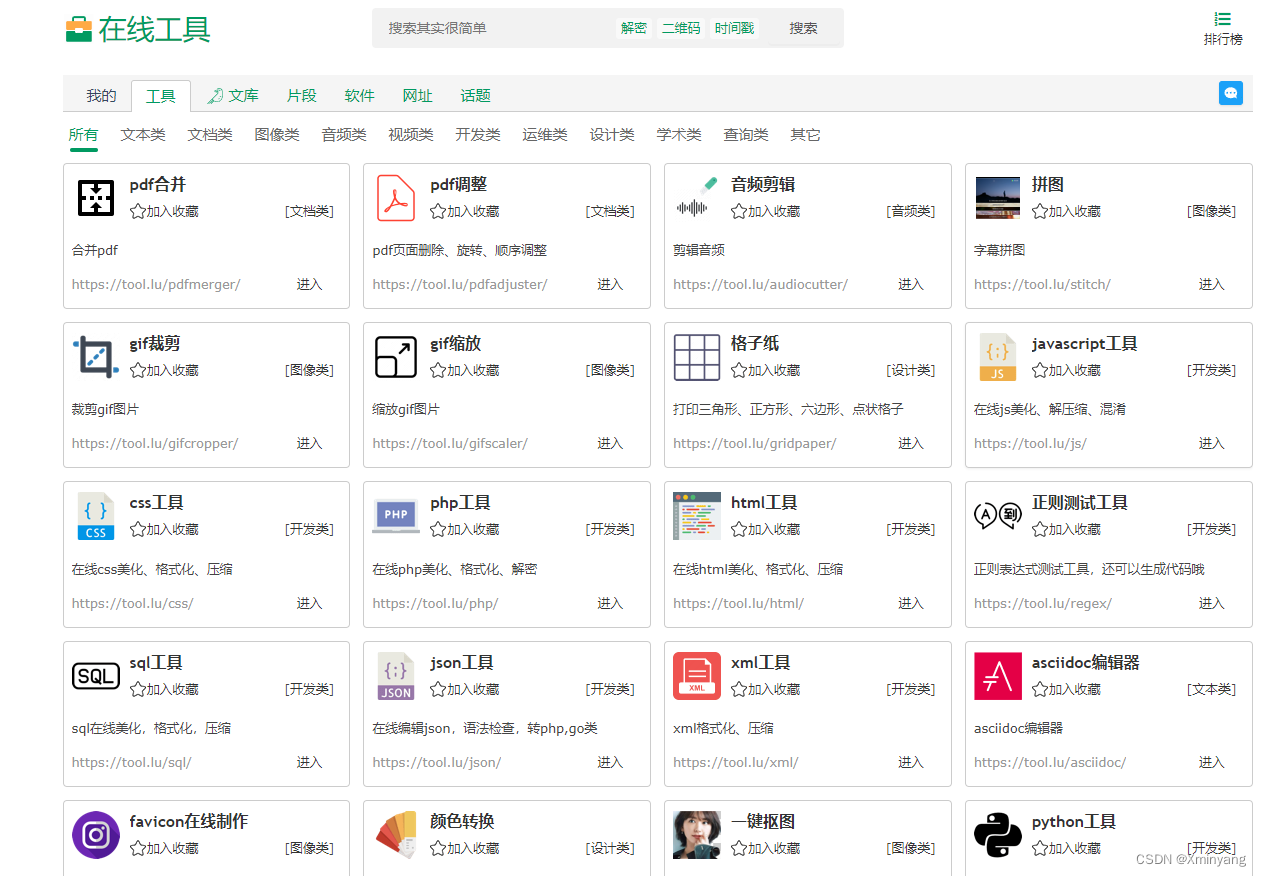
在线硬核工具
uniCloud
Qtcreator sets multiple qmake
随机推荐
What does intermediate software evaluator test
China Southern Airlines pa3.1
软考中级电子商务师含金量高嘛?
seata 1.3.0 四种模式解决分布式事务(AT、TCC、SAGA、XA)
Those confusing concepts (3): function and class
P2788 math 1 - addition and subtraction
P1223 queuing for water /1319: [example 6.1] queuing for water
Get pictures through opencv, change channels and save them
一些线上学术报告网站与机器学习视频
JSON format query of MySQL
Arduino receives and sends strings
Compile QT project script with qmake
PHP \ newline cannot be output
What is an intermediate network engineer? What is the main test and what is the use?
CSAPP Bomb Lab 解析
Use load_ decathlon_ Datalist (Monai) fast loading JSON data
[pytorch 07] hands on deep learning chapter_ Preliminaries/ndarray exercises hands-on version
How much review time does it usually take to take the intermediate soft exam?
2022年7月10日“五心公益”活动通知+报名入口(二维码)
2022年上半年5月网络工程师试题及答案