当前位置:网站首页>Implementation of AVL tree
Implementation of AVL tree
2022-07-06 18:44:00 【m0_ sixty-two million four hundred and six thousand two hundred】
One ,AvL The concept of tree :
Although binary search tree can shorten the search efficiency , However, if the data is ordered or close to ordered, the binary search tree will degenerate into a single branch tree , Find element equivalent
To search for elements in the sequence table , inefficiency . therefore , Two Russian mathematicians G.M.Adelson-Velskii and E.M.Landis stay 1962 year
A method for solving the above problems is invented : When a new node is inserted into the binary search tree , If the height of the left and right subtrees of each node can be guaranteed
The absolute value of the difference does not exceed 1( You need to adjust the nodes in the tree ), You can reduce the height of the tree , This reduces the average search length .
A tree AVL Trees or empty trees , Or a binary search tree with the following properties :
Its left and right subtrees are AVL Trees
The difference between the height of the left and right subtrees ( It's called equilibrium factor ) The absolute value of is not more than 1(-1/0/1)
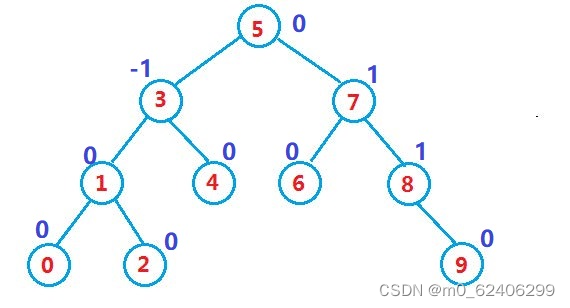
If a binary search tree is highly balanced , It is AVL Trees . If it has n Nodes , Its height can be maintained at , When searching
The complexity O(logn )
Two ,AVL Definition of tree node
template<class T>
struct AVLTreeNode
{
AVLTreeNode(const T& data)
: _pLeft(nullptr), _pRight(nullptr), _pParent(nullptr)
, _data(data), _bf(0)
{}
AVLTreeNode<T>* _pLeft; // The left child of this node
AVLTreeNode<T>* _pRight; // The right child of this node
AVLTreeNode<T>* _pParent; // The parents of this node
T _data;
int _bf; // The equilibrium factor of this node
};3、 ... and ,Avl Insertion of tree nodes
AVL The tree is based on the binary search tree and introduces the balance factor , therefore AVL The tree can also be regarded as a binary search tree . that AVL Insertion of trees
The process can be divided into two steps :
1. Insert the new node as a binary search tree
2. Adjust the balance factor of the node
bool Insert(const T& data)
{
// 1. First, insert the node into according to the rules of binary search tree AVL In the tree
// ...
// 2. After the new node is inserted ,AVL The balance of the tree may be destroyed , At this point, you need to update the balance factor , And detect whether it destroys
AVL Trees
// Balance
/*
pCur After inserting ,pParent The balance factor must be adjusted , Before inserting ,pParent
The equilibrium factor is divided into three cases :-1,0, 1, There are two situations :
1. If pCur Insert into pParent The left side of the , Just give pParent The equilibrium factor of -1 that will do
2. If pCur Insert into pParent The right side of the , Just give pParent The equilibrium factor of +1 that will do
here :pParent There are three possible situations for the equilibrium factor of :0, Plus or minus 1, Plus or minus 2
1. If pParent The equilibrium factor of 0, Description before insertion pParent The balance factor is positive and negative 1, After insertion, it is adjusted to 0, this
Time to satisfy
AVL Properties of trees , Insert the success
2. If pParent The balance factor is positive and negative 1, Description before insertion pParent The equilibrium factor must be 0, It is updated to plus or minus after insertion
1, this
Time and space pParent Increase the height of the tree for the root , Need to continue to update up
3. If pParent The balance factor is positive and negative 2, be pParent The equilibrium factor of violates the properties of the equilibrium tree , It needs to be rotated
Handle
*/
while (pParent)
{
// Update the balance factor of parents
if (pCur == pParent->_pLeft)
pParent->_bf--;
else
pParent->_bf++;
// The balance factor of parents was detected after updating
if (0 == pParent->_bf)
break;
else if (1 == pParent->_bf || -1 == pParent->_bf)
{
// The balance factor of parents before insertion is 0, The balance of parents after insertion is 1 perhaps -1 , It shows that parents are rooted in
Binary tree
// The height of the has been increased by one layer , Therefore, we need to continue to adjust upward
pCur = pParent;
pParent = pCur->_pParent;
}
else
{
// The balance factor of parents is positive and negative 2, A violation of the AVL The balance of the tree , It is necessary to pParent
// Rotate the root tree
if(2 == pParent->_bf)
{
// ...
}
else
{
//.......
}
}
}
return true;
}Four ,AVL The rotation of the tree
If in a tree that was originally balanced AVL Insert a new node into the tree , May cause imbalance , At this point, the structure of the tree must be adjusted , Balance it
turn . According to the insertion position of the node ,AVL There are four kinds of tree rotation :
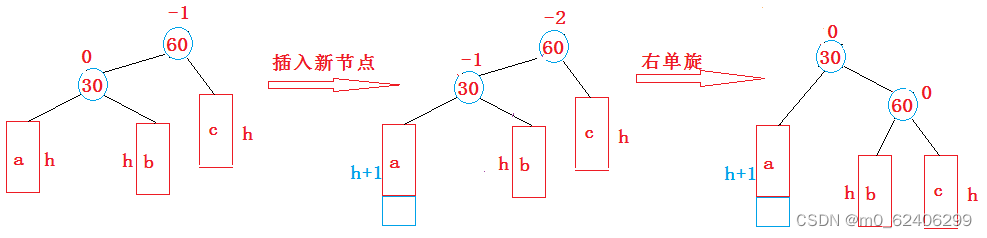
1. The new node is inserted to the left of the higher left subtree --- Left, left : Right single spin
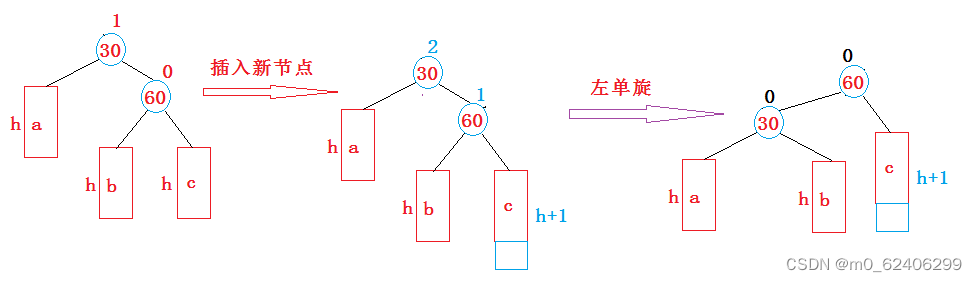
2. The new node is inserted to the right of the higher subtree ———— Right, right : Left spin
 3. The new node is inserted to the right of the higher left subtree --- about : First left single spin, then right single spin
3. The new node is inserted to the right of the higher left subtree --- about : First left single spin, then right single spin
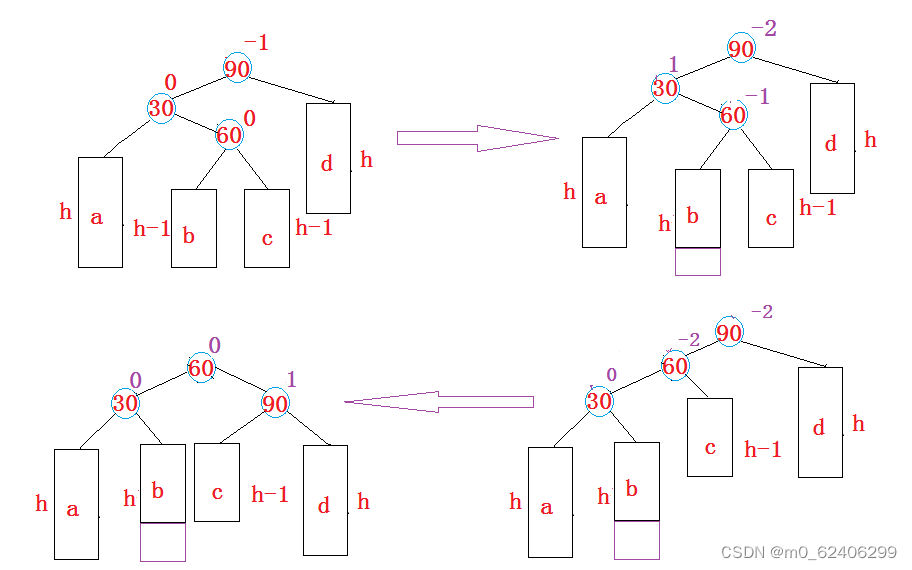
Turn double spin into single spin and then rotate , namely : First pair 30 Make a left spin , And then to 90 Make a right spin , After the rotation is completed, consider the update of the balance factor
4. The new node is inserted to the left of the higher right subtree --- Right to left : First right single spin, then left single spin
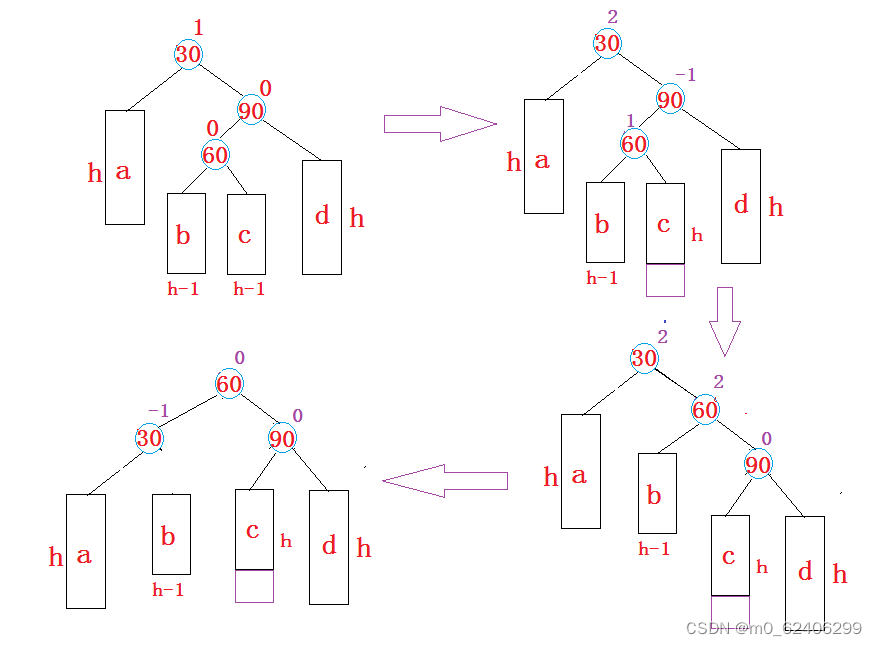
Reference right left double rotation .
summary :
If pParent The subtree with roots is unbalanced , namely pParent The equilibrium factor of 2 perhaps -2, Consider the following
1. pParent The equilibrium factor of 2, explain pParent The height of the right subtree , set up pParent The root of the right subtree of is pSubR
When pSubR The equilibrium factor of 1 when , Execute left single rotation
When pSubR The equilibrium factor of -1 when , Perform right and left double rotation
2. pParent The equilibrium factor of -2, explain pParent The height of the left subtree , set up pParent The root of the left subtree of is pSubL
When pSubL The equilibrium factor of -1 yes , Execute right single rotation
When pSubL The equilibrium factor of 1 when , Perform left and right double rotation
When the rotation is complete , primary pParent Reduce the height of the subtree of the root , It's balanced , No need to update up .
边栏推荐
猜你喜欢
Self supervised heterogeneous graph neural network with CO comparative learning
Docker installation redis

2022-2024年CIFAR Azrieli全球学者名单公布,18位青年学者加入6个研究项目
Medical image segmentation
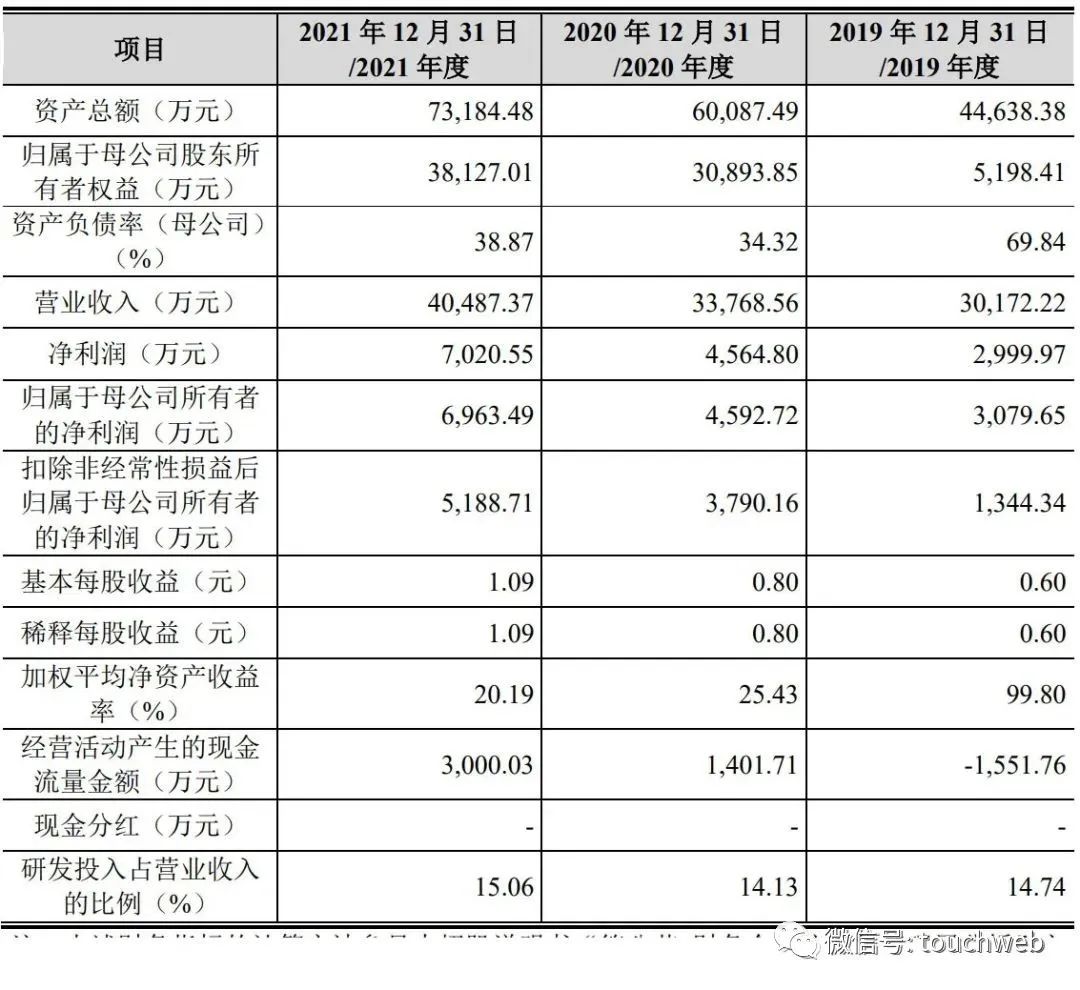
朗坤智慧冲刺科创板:年营收4亿 拟募资7亿
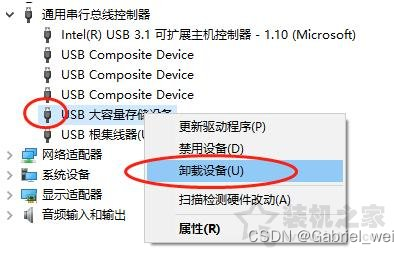
There is a sound prompt when inserting a USB flash disk under win10 system, but the drive letter is not displayed

44 colleges and universities were selected! Publicity of distributed intelligent computing project list
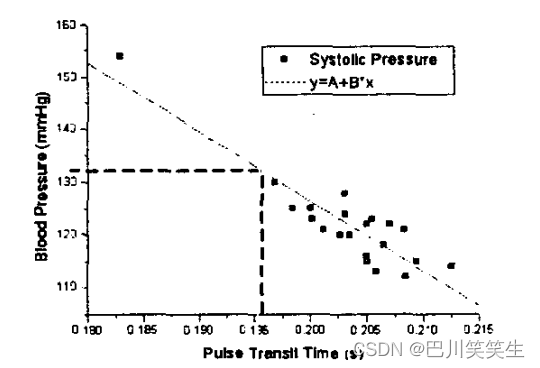
用于远程医疗的无创、无袖带血压测量【翻译】
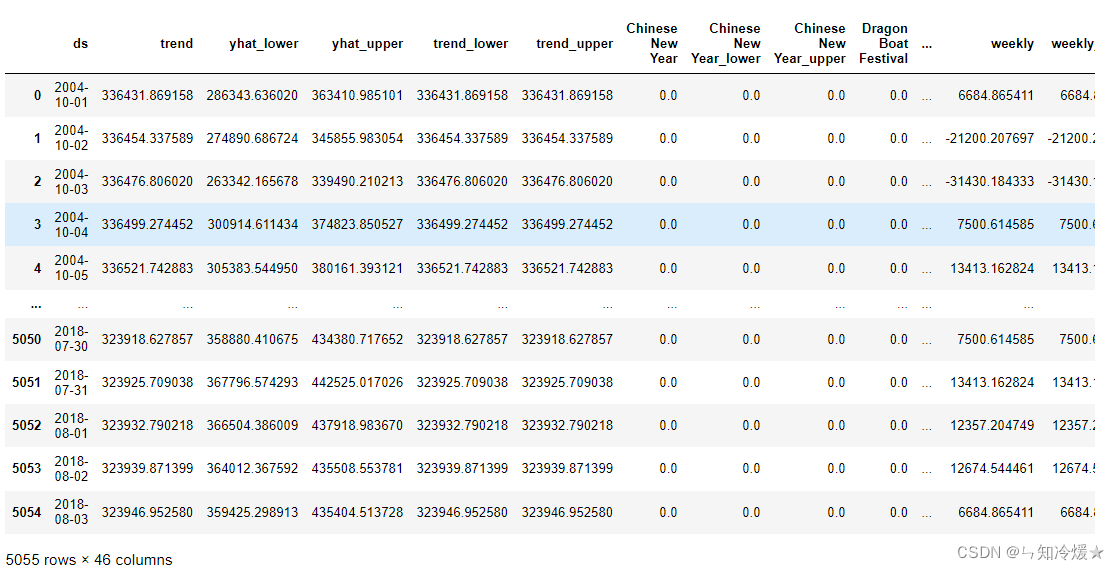
Introduction and case analysis of Prophet model
根据PPG估算血压利用频谱谱-时间深度神经网络【翻】
随机推荐
小程序在产业互联网中的作用
Markdown syntax for document editing (typera)
测试123
Test 123
STM32+ESP8266+MQTT协议连接OneNet物联网平台
使用cpolar建立一个商业网站(1)
图之广度优先遍历
CRMEB 商城系统如何助力营销?
Cobra quick start - designed for command line programs
重磅硬核 | 一文聊透对象在 JVM 中的内存布局,以及内存对齐和压缩指针的原理及应用
华为0基金会——图片整理
win10系统下插入U盘有声音提示却不显示盘符
Nuc11 cheetah Canyon setting U disk startup
Blue Bridge Cup real question: one question with clear code, master three codes
Celery best practices
手写一个的在线聊天系统(原理篇1)
There is a sound prompt when inserting a USB flash disk under win10 system, but the drive letter is not displayed
Describe the process of key exchange
测试行业的小伙伴,有问题可以找我哈。菜鸟一枚~
bonecp使用数据源