当前位置:网站首页>最长的可整合子数组的长度
最长的可整合子数组的长度
2022-07-04 18:48:00 【GreyZeng】
最长的可整合子数组的长度
作者:Grey
原文地址: 最长的可整合子数组的长度
题目链接
描述
先给出可整合数组的定义:如果一个数组在排序之后,每相邻两个数的差的绝对值都为1,或者该数组长度为1,则该数组为可整合数组。例如,
[5, 3, 4, 6, 2]排序后为[2, 3, 4, 5, 6],符合每相邻两个数差的绝对值都为1,所以这个数组为可整合数组,给定一个数组arr, 请返回其中最大可整合子数组的长度。
例如,[5, 5, 3, 2, 6, 4, 3]的最大可整合子数组为[5, 3, 2, 6, 4],所以请返回5
数据范围:0 <n≤100000,数组中每个数都满足0≤val≤10^9
要求:时间复杂度为O(n^2),空间复杂度为O(n)
进阶:时间复杂度O(nlogn),空间复杂度O(n)
暴力解法
枚举每个子数组,然后对每个子数组进行排序,然后判断是否为可整合数组,完整代码如下
public static int getLIL1(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int len = 0;
// O(N^3 * log N)
for (int start = 0; start < arr.length; start++) {
for (int end = start; end < arr.length; end++) {
if (isIntegrated(arr, start, end)) {
len = Math.max(len, end - start + 1);
}
}
}
return len;
}
public static boolean isIntegrated(int[] arr, int left, int right) {
int[] newArr = Arrays.copyOfRange(arr, left, right + 1); // O(N)
Arrays.sort(newArr); // O(N*logN)
for (int i = 1; i < newArr.length; i++) {
if (newArr[i - 1] != newArr[i] - 1) {
return false;
}
}
return true;
}
暴力解法的时间复杂度是O(N^3*logN),显然超时。
优化解
某个数组如果属于可整合数组,则这个数组一定符合如下两个条件:
第一个条件:数组中的元素没有重复。
第二个条件:数组中的最大值和最小值的差值等于数组元素个数-1。
如果满足上述两个条件,一定是可整合数组。
我们可以通过设置一个HashSet来判断元素是否重复。
完整代码
public static int getLIL2(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
int len = 0;
int max = 0;
int min = 0;
HashSet<Integer> set = new HashSet<Integer>();
for (int l = 0; l < arr.length; l++) {
set.clear();
max = arr[l];
min = arr[l];
for (int r = l; r < arr.length; r++) {
if (set.contains(arr[r])) {
break;
}
set.add(arr[r]);
max = Math.max(max, arr[r]);
min = Math.min(min, arr[r]);
if (max - min == r - l) {
len = Math.max(len, r - l + 1);
}
}
}
return len;
}
整个算法时间复杂度O(N*logN),符合要求。
更多
边栏推荐
- Integretee integrates into Moonriver through xcm, bringing enterprise class privacy solutions to its ecosystem
- 实战模拟│JWT 登录认证
- 【历史上的今天】7 月 4 日:第一本电子书问世;磁条卡的发明者出生;掌上电脑先驱诞生
- Utilisation de la barre de progression cbcggprogressdlgctrl utilisée par BCG
- How is the entered query SQL statement executed?
- Ziguang zhanrui completed the first 5g R17 IOT NTN satellite on the Internet of things in the world
- Cbcgpprogressdlg progress bar used by BCG
- 同事的接口文档我每次看着就头大,毛病多多。。。
- Why is the maximum speed the speed of light
- 华为云云商店首页 Banner 资源位申请
猜你喜欢
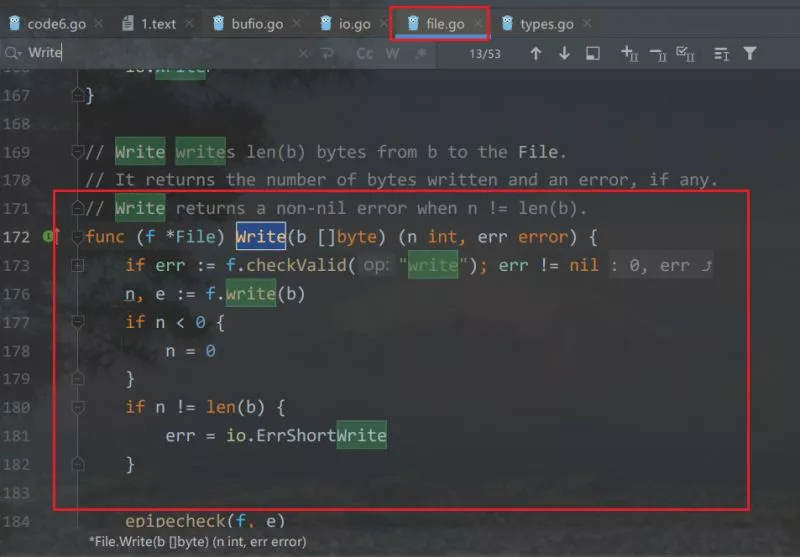
一文搞懂Go语言中文件的读写与创建
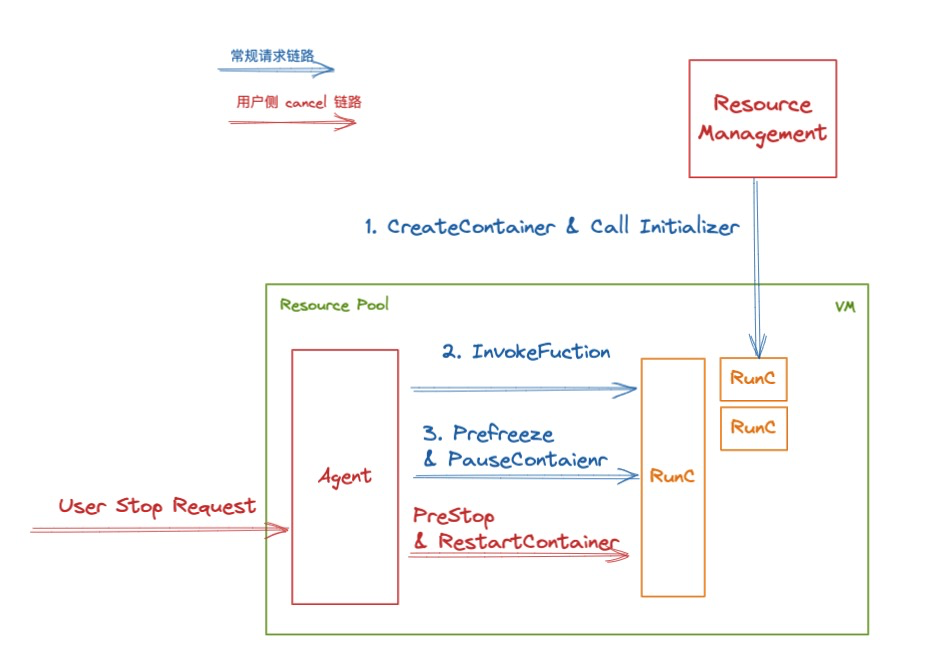
解密函数计算异步任务能力之「任务的状态及生命周期管理」
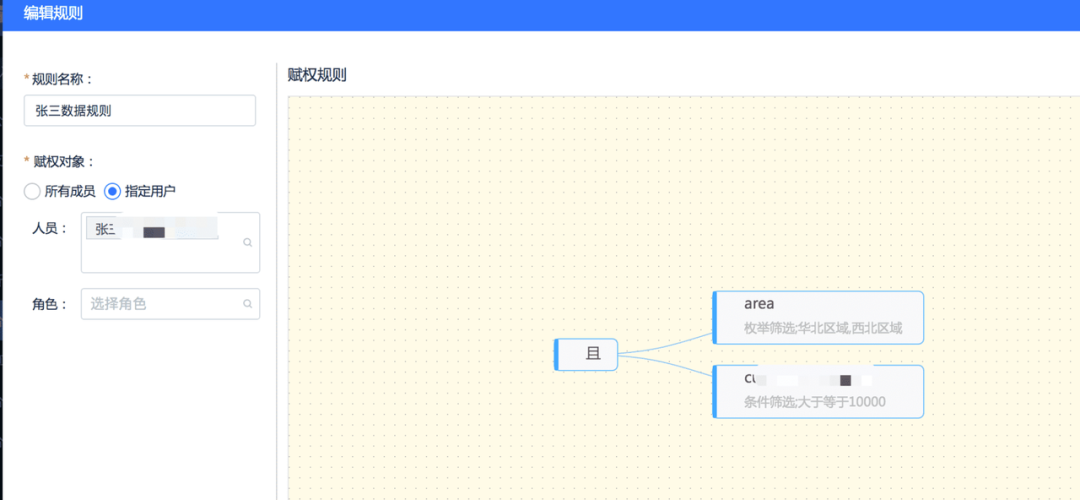
应用实践 | 蜀海供应链基于 Apache Doris 的数据中台建设
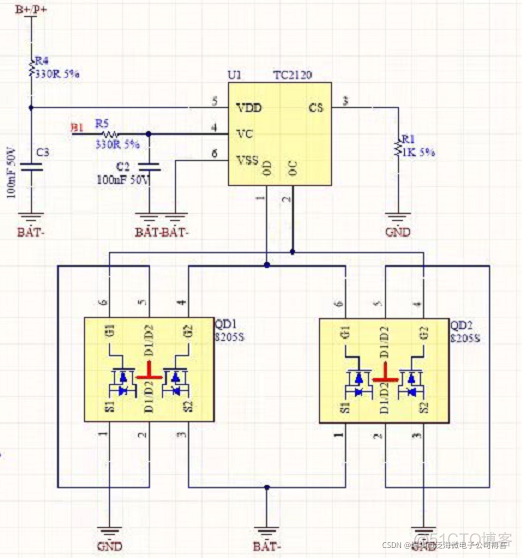
FS4061A升压8.4V充电IC芯片和FS4061B升压12.6V充电IC芯片规格书datasheet
CANN算子:利用迭代器高效实现Tensor数据切割分块处理
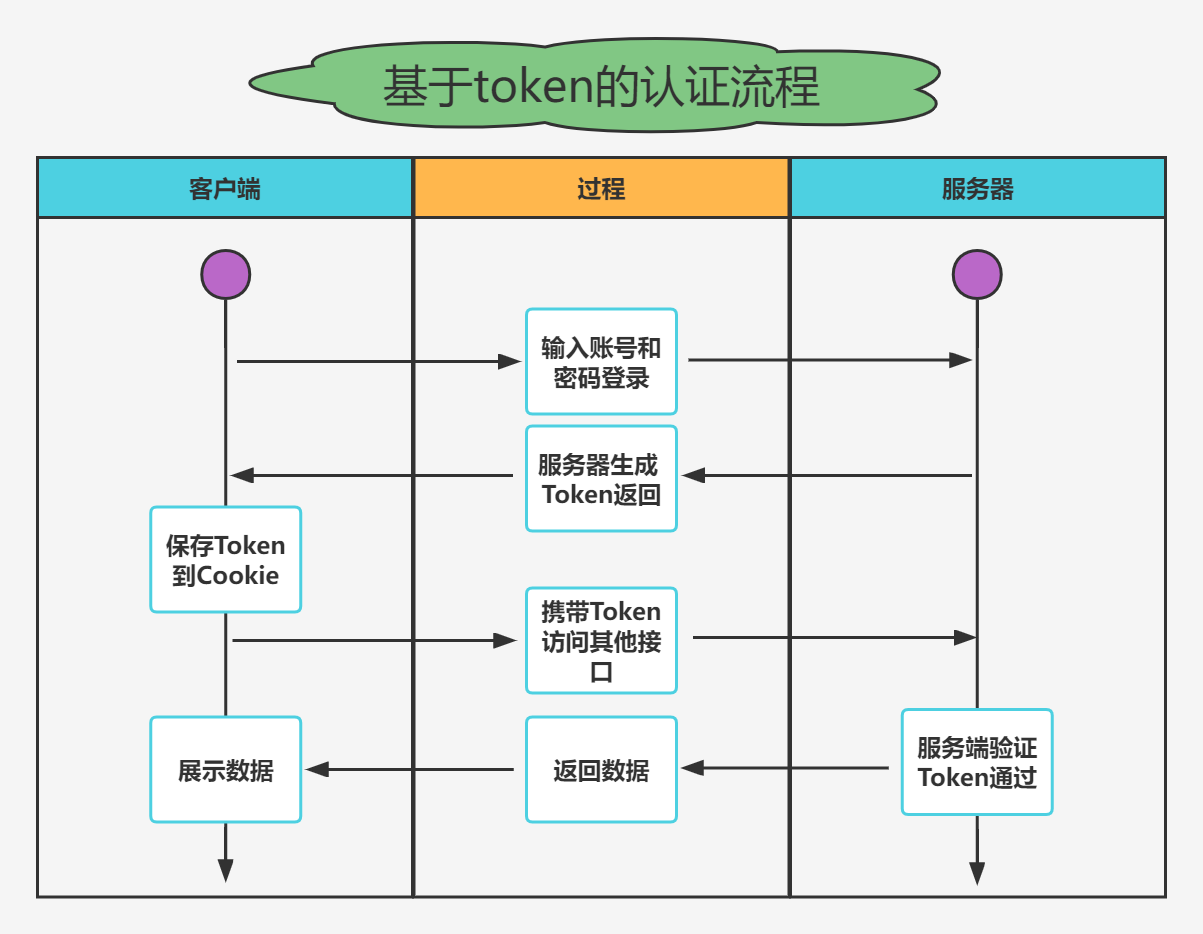
实战模拟│JWT 登录认证

ICML 2022 | Meta提出鲁棒的多目标贝叶斯优化方法,有效应对输入噪声
![NLP, vision, chip What is the development direction of AI? Release of the outlook report of Qingyuan Association [download attached]](/img/79/82763392e74d102921b4e8e601d4c6.png)
NLP, vision, chip What is the development direction of AI? Release of the outlook report of Qingyuan Association [download attached]
Dark horse programmer - software testing - stage 08 2-linux and database-23-30-process port related, modify file permissions, obtain port number information, program and process related operations, Li
![NLP、视觉、芯片...AI重点方向发展几何?青源会展望报告发布[附下载]](/img/79/82763392e74d102921b4e8e601d4c6.png)
NLP、视觉、芯片...AI重点方向发展几何?青源会展望报告发布[附下载]
随机推荐
Installation and use of VMware Tools and open VM tools: solve the problems of incomplete screen and unable to transfer files of virtual machines
记一次 .NET 某工控数据采集平台 线程数 爆高分析
2022 version of stronger jsonpath compatibility and performance test (snack3, fastjson2, jayway.jsonpath)
【深度学习】一文看尽Pytorch之十九种损失函数
[QNX hypervisor 2.2 user manual]6.3.1 factory page and control page
凌云出海记 | 沐融科技&华为云:打造非洲金融SaaS解决方案样板
Detailed explanation of Audi EDI invoice message
华为nova 10系列支持应用安全检测功能 筑牢手机安全防火墙
What financial products can you buy with a deposit of 100000 yuan?
1009 product of polynomials (25 points) (PAT class a)
AP8022开关电源小家电ACDC芯片离线式开关电源IC
#夏日挑战赛#带你玩转HarmonyOS多端钢琴演奏
Swagger suddenly went crazy
需求开发思考
NLP, vision, chip What is the development direction of AI? Release of the outlook report of Qingyuan Association [download attached]
凌云出海记 | 文华在线&华为云:打造非洲智慧教学新方案
华为云云商店首页 Banner 资源位申请
c# . Net MVC uses Baidu ueditor rich text box to upload files (pictures, videos, etc.)
Niuke Xiaobai month race 7 F question
The company needs to be monitored. How do ZABBIX and Prometheus choose? That's the right choice!