当前位置:网站首页>Visual Studio 插件之CodeMaid自动整理代码
Visual Studio 插件之CodeMaid自动整理代码
2022-07-07 17:31:00 【执着的涛】
介绍
当我们平时 coding 时,代码的格式千奇百怪,不知道快捷键的同学,可能还在徒手敲敲空格或者缩进。知道快捷的同学,每次写完后,会按下快捷键,单有时还会忘记,使得阅读代码时不太便于理解,更重要的是也影响了我们的开发效率。CodeMaid 的出现,可以快速解放你的双手,提高你的开发效率,自动格式化你的代码、清理排序命名空间,当然他也是免费开源的。
Visual Studio神级插件之CodeMaid自动整理你的代码_菜鸟厚非的博客-CSDN博客_codemaid怎么使用
边栏推荐
- Responsibility chain model - unity
- 【牛客网刷题系列 之 Verilog进阶挑战】~ 多bit MUX同步器
- 凌云出海记 | 赛盒&华为云:共助跨境电商行业可持续发展
- ASP. Net kindergarten chain management system source code
- The project manager's "eight interview questions" is equal to a meeting
- 9 atomic operation class 18 Rohan enhancement
- 2022.07.04
- ASP.NET幼儿园连锁管理系统源码
- ASP. Net gymnasium integrated member management system source code, free sharing
- Numpy——2.数组的形状
猜你喜欢
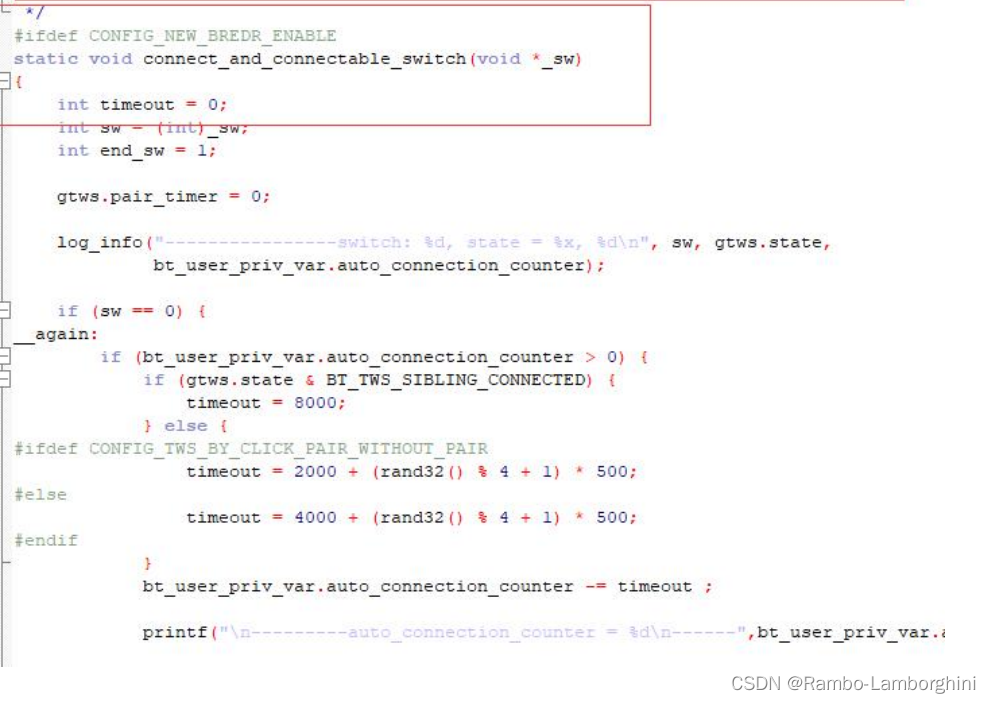
杰理之发起对耳配对、回连、开启可发现、可连接的轮循函数【篇】

PV static creation and dynamic creation
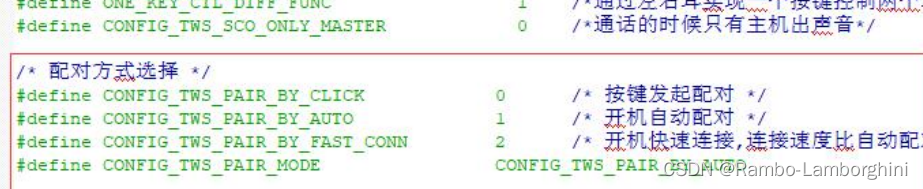
杰理之关于 TWS 配对方式配置【篇】
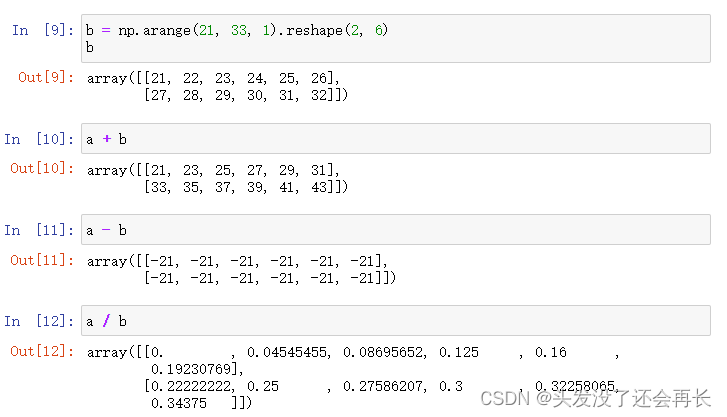
Numpy——2.数组的形状
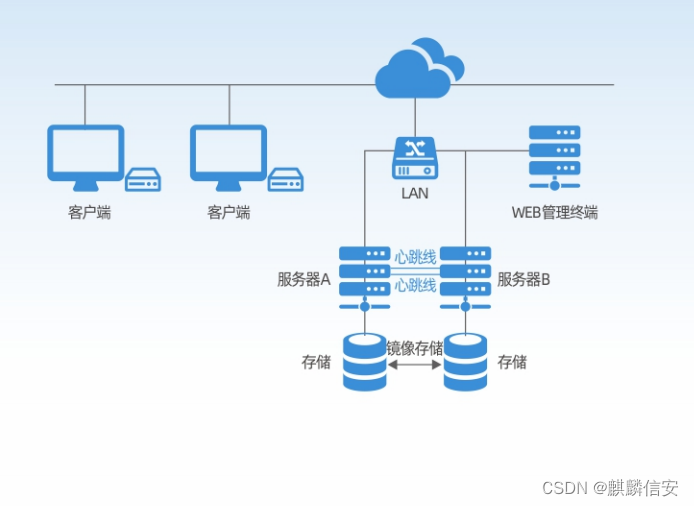
Empowering smart power construction | Kirin Xin'an high availability cluster management system to ensure the continuity of users' key businesses

Kunpeng developer summit 2022 | Kirin Xin'an and Kunpeng jointly build a new ecosystem of computing industry

Kirin Xin'an joins Ningxia commercial cipher Association

2022.07.04

2022.07.02
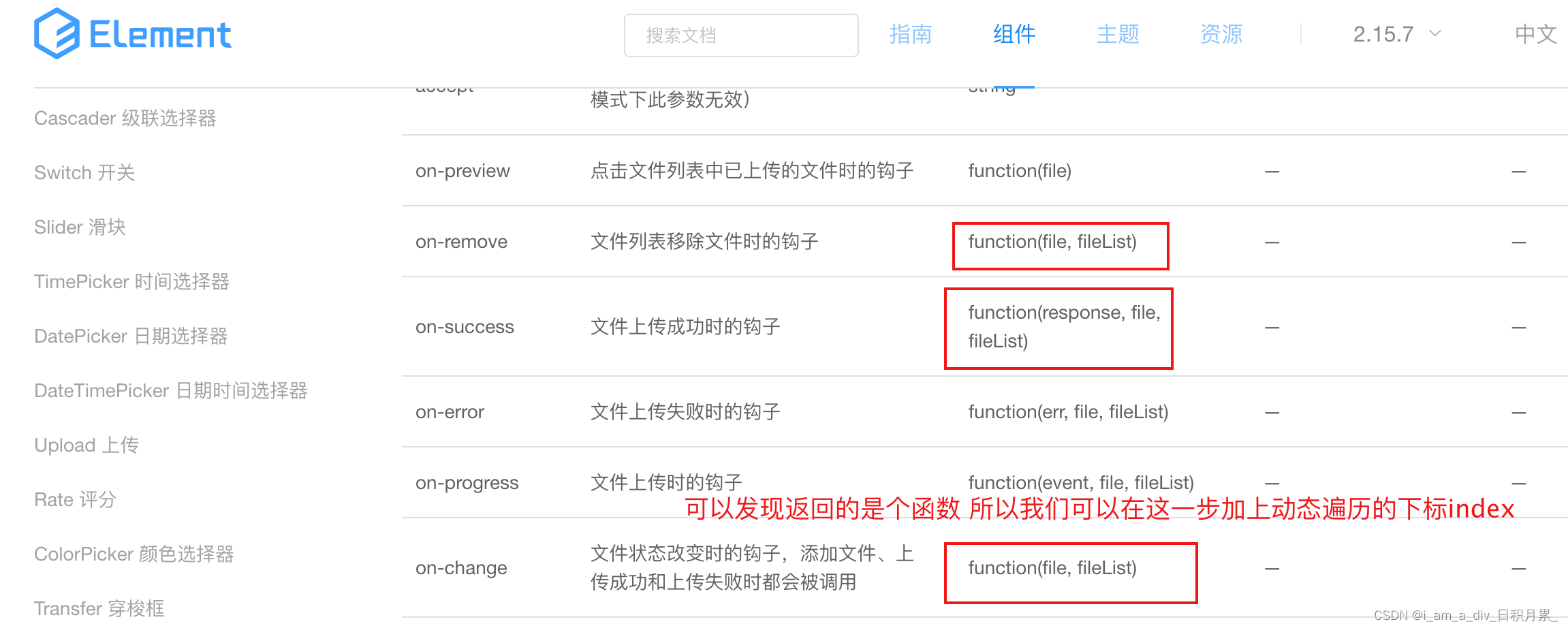
el-upload上传组件的动态添加;el-upload动态上传文件;el-upload区分文件是哪个组件上传的。
随机推荐
Initial experience of cache and ehcache "suggestions collection"
歌单11111
杰理之快速配对,不支持取消配对【篇】
谷歌seo外链Backlinks研究工具推荐
MySQL、sqlserver oracle数据库连接方式
Uvalive – 4621 CAV greed + analysis "suggestions collection"
R语言dplyr包mutate_at函数和min_rank函数计算dataframe中指定数据列的排序序号值、名次值、将最大值的rank值赋值为1
Empowering smart power construction | Kirin Xin'an high availability cluster management system to ensure the continuity of users' key businesses
Netease Yunxin participated in the preparation of the standard "real time audio and video service (RTC) basic capability requirements and evaluation methods" issued by the Chinese Academy of Communica
how to prove compiler‘s correctness
# 欢迎使用Markdown编辑器
Make this crmeb single merchant wechat mall system popular, so easy to use!
PMP对工作有益吗?怎么选择靠谱平台让备考更省心省力!!!
R语言dplyr包select函数、group_by函数、filter函数和do函数获取dataframe中指定因子变量中指定水平中特定数值数据列的值第三大的值
2022.07.05
POJ 1182: food chain (parallel search) [easy to understand]
Jürgen Schmidhuber回顾LSTM论文等发表25周年:Long Short-Term Memory. All computable metaverses. Hierarchical reinforcement learning (RL). Meta-RL. Abstractions in generative adversarial RL. Soccer learn
LeetCode 515(C#)
爬虫实战(七):爬王者英雄图片
Where does brain hole come from? New research from the University of California: creative people's neural connections will "take shortcuts"