当前位置:网站首页>1013. Divide the array into three parts equal to and
1013. Divide the array into three parts equal to and
2022-07-06 16:07:00 【mrbone9】
Address :
Power button  https://leetcode-cn.com/problems/partition-array-into-three-parts-with-equal-sum/
https://leetcode-cn.com/problems/partition-array-into-three-parts-with-equal-sum/
subject :
Give you an array of integers arr, Only can it be divided into three and equal Non empty Return only when partial true, Otherwise return to false.
Formally , If you can find the index i + 1 < j And meet (arr[0] + arr[1] + ... + arr[i] == arr[i + 1] + arr[i + 2] + ... + arr[j - 1] == arr[j] + arr[j + 1] + ... + arr[arr.length - 1]) You can divide the array into three equal parts .
Example 1:
| Input :arr = [0,2,1,-6,6,-7,9,1,2,0,1] Output :true explain :0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1 |
Example 2:
| Input :arr = [0,2,1,-6,6,7,9,-1,2,0,1] Output :false |
Example 3:
| Input :arr = [3,3,6,5,-2,2,5,1,-9,4] Output :true explain :3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4 |
Tips :
| 3 <= arr.length <= 5 * 104 -104 <= arr[i] <= 104 |
source : Power button (LeetCode)
link :https://leetcode-cn.com/problems/partition-array-into-three-parts-with-equal-sum
Copyright belongs to the network . For commercial reprint, please contact the official authority , Non-commercial reprint please indicate the source .
Ideas :
Since it is divided into three groups and , Then first of all, ask and , Every part and is its 1/3
If the sum cannot be 3 to be divisible by , direct false
Use double pointers to separate from the array [0], Array [len-1] Close to the middle , Find the left value and , Right value sum
Intermediate and = The sum of the - L value and - Right value sum
The pit here is :
1. Can't find L value and = Right value sum , Just jump out of the loop , At this time, the left value has not reached 1/3, Nature needs to continue to accumulate
2. Can't find L value and = Right value sum , And equal to 1/3 , Jump out of the loop and find the middle sum is also equal , There is a possibility that
The sum of the = 0, L value and = Right value sum = 0, such as [1,-1, -1, 1]
So it also depends on whether the number of the middle number is 0, Only when it is not, can we continue to judge
There are many calculations in this way , And consider more boundaries , The test case has a high probability of error
Another idea is relatively simple , Reference method 2
Method 1 、 Double pointer summation
bool canThreePartsEqualSum(int* arr, int arrSize){
int goal = 0;
int lsum = 0, msum = 0, rsum = 0;
int sums = 0;
int cnt = arrSize;
int i,j;
for(i=0; i<arrSize; i++)
sums += arr[i];
if(sums % 3 != 0)
return false;
goal = sums/3;
i = 0;
j = arrSize - 1;
lsum += arr[i];
rsum += arr[arrSize-1];
cnt-=2;
while( cnt > 0)
{
if(lsum != goal)
{
i++;
lsum += arr[i];
cnt--;
}
if(rsum != goal)
{
j--;
rsum += arr[j];
cnt--;
}
if(lsum == goal && lsum == rsum)
break;
}
msum = sums - lsum - rsum;
if(cnt > 0 && lsum == msum && rsum == msum)
return true;
else
return false;
}Method 2 、 Find the number of multiples
We know 1/3 And , Then at least there is 3 Such a sum , There may also be more , For example, He Wei 0 perhaps 3n A combination like this
So we only need two steps to complete
1. Statistical sum
2. Ask again 1/3 And , Number of Statistics ++, If the number of statistics is less than 3 , That's it false
bool canThreePartsEqualSum(int* arr, int arrSize){
int sum = 0;
int tmp = 0;
int goal = 0;
int cnt = 0;
int i;
for(i=0; i<arrSize; i++)
sum += arr[i];
if(sum % 3 != 0)
return false;
goal = sum / 3;
for(i=0; i<arrSize; i++)
{
tmp += arr[i];
if(tmp == goal)
{
cnt++;
tmp = 0;
}
}
if(cnt < 3)
return false;
return true;
}边栏推荐
- Opencv learning log 15 count the number of solder joints and output
- Basic Q & A of introductory C language
- Quick to typescript Guide
- 【练习-4】(Uva 11988)Broken Keyboard(破损的键盘) ==(链表)
- Nodejs crawler
- 1010 things that college students majoring in it must do before graduation
- 【练习-5】(Uva 839)Not so Mobile(天平)
- [exercise-3] (UVA 442) matrix chain multiplication
- Penetration test (7) -- vulnerability scanning tool Nessus
- Research Report of exterior wall insulation system (ewis) industry - market status analysis and development prospect prediction
猜你喜欢
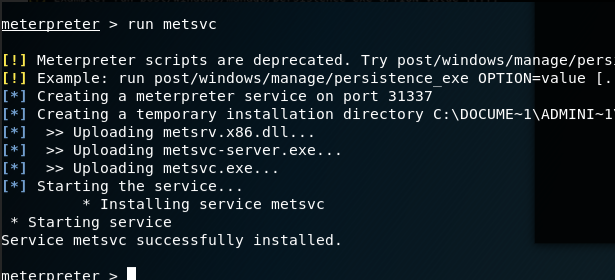
渗透测试 ( 3 ) --- Metasploit Framework ( MSF )

Penetration testing (5) -- a collection of practical skills of scanning King nmap and penetration testing tools
![mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’](/img/e6/f4a696179282fe1f4193410c5a493a.png)
mysql导入数据库报错 [Err] 1273 – Unknown collation: ‘utf8mb4_0900_ai_ci’
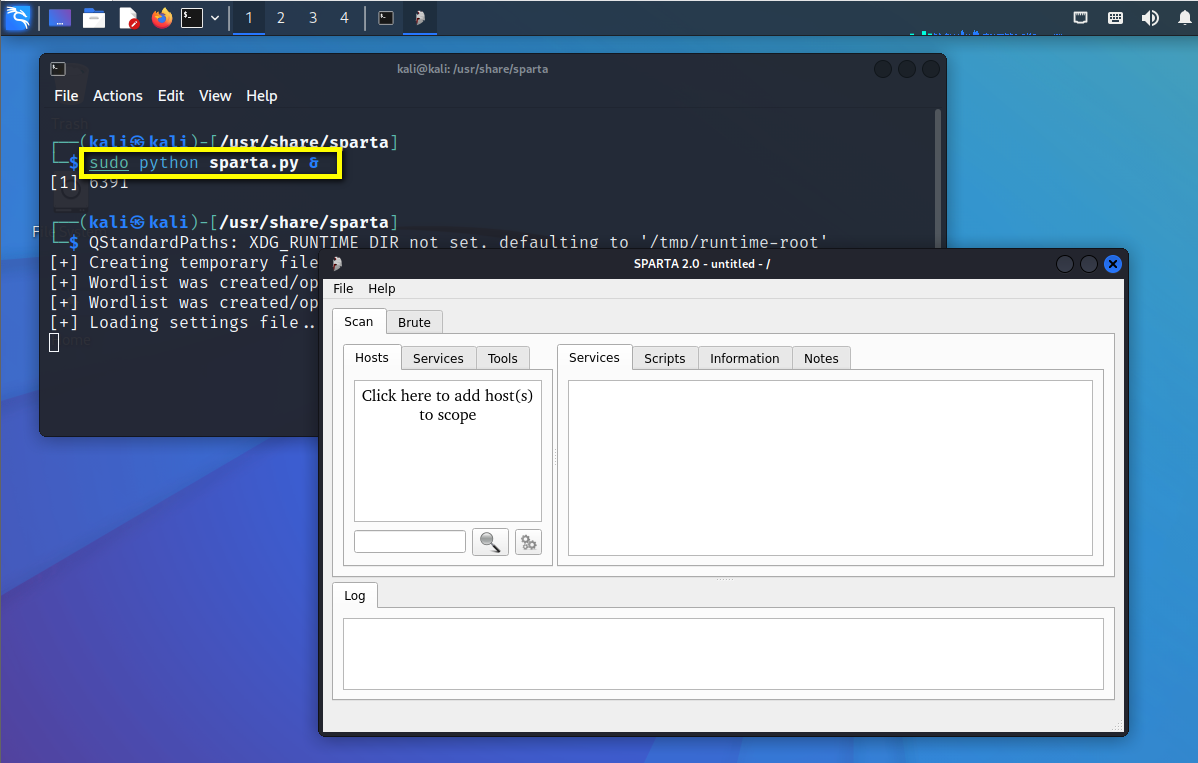
滲透測試 ( 1 ) --- 必備 工具、導航

Essai de pénétration (1) - - outils nécessaires, navigation

B - 代码派对(女生赛)
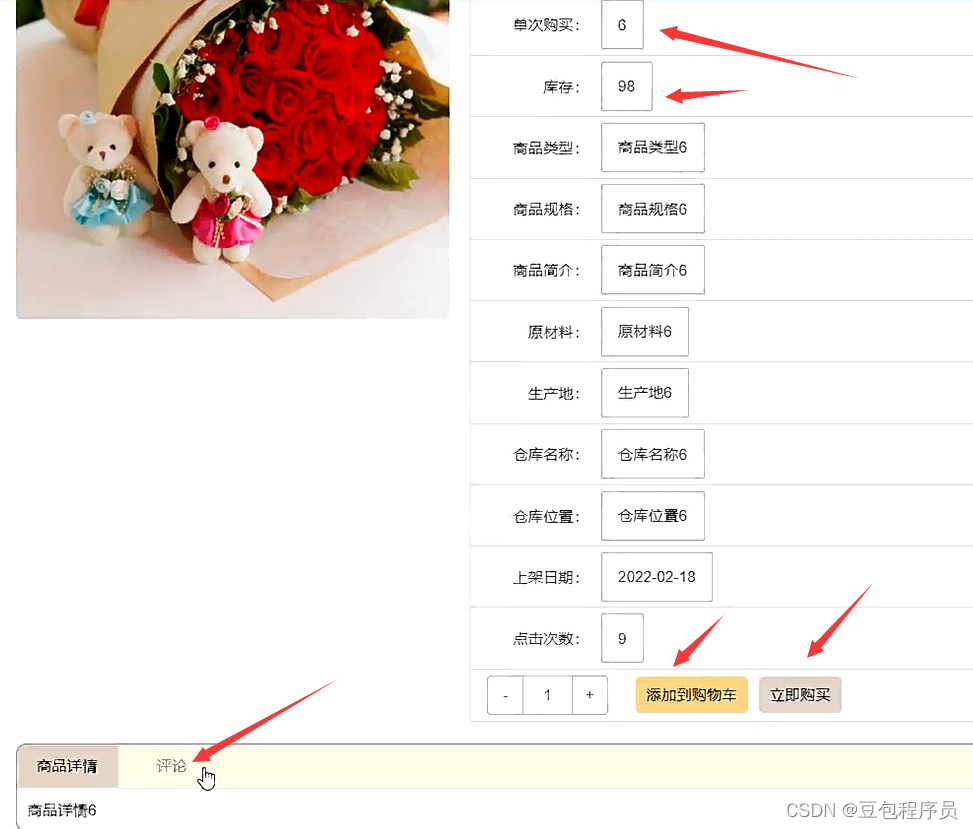
Nodejs+vue online fresh flower shop sales information system express+mysql
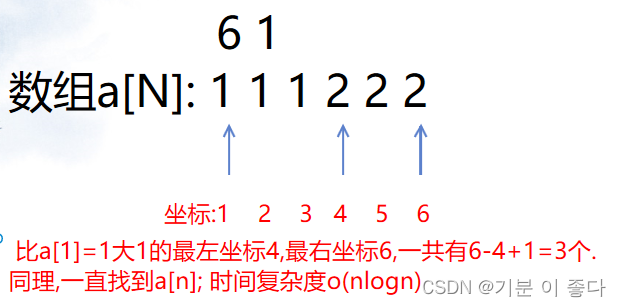
Luogu P1102 A-B number pair (dichotomy, map, double pointer)
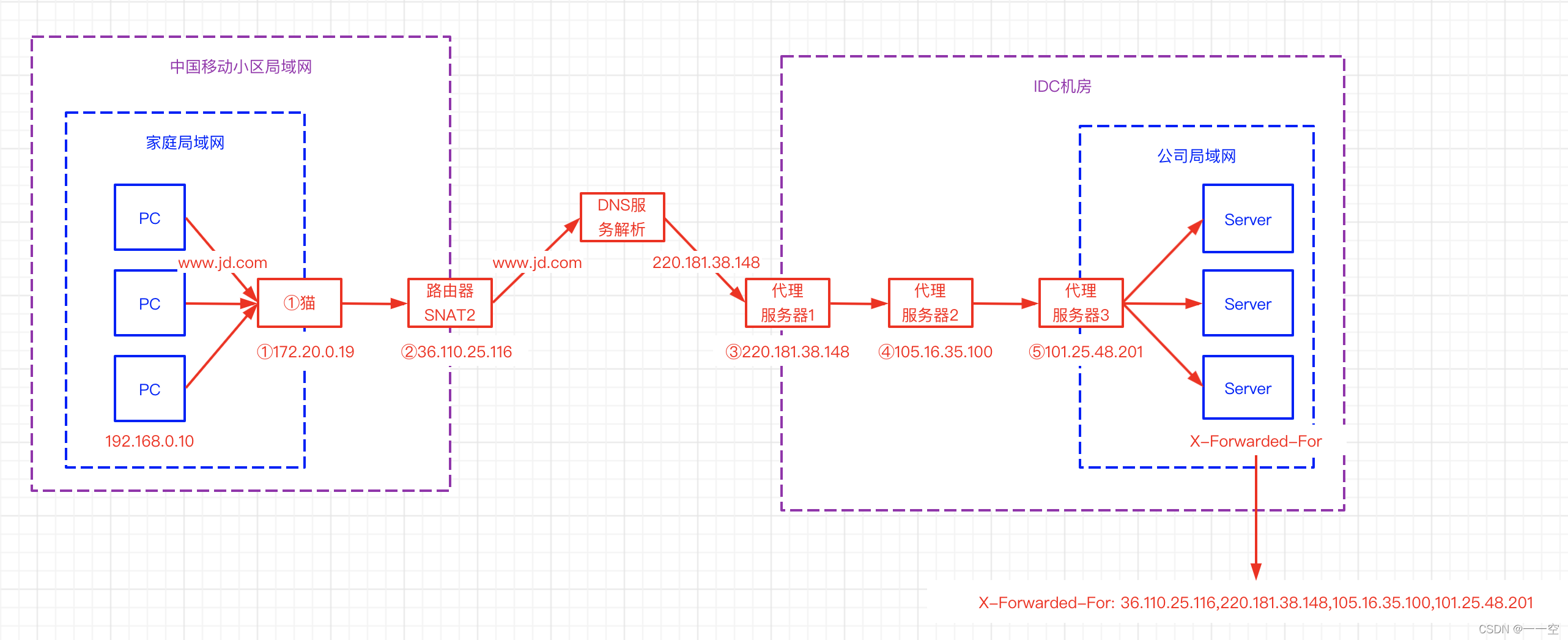
X-Forwarded-For详解、如何获取到客户端IP
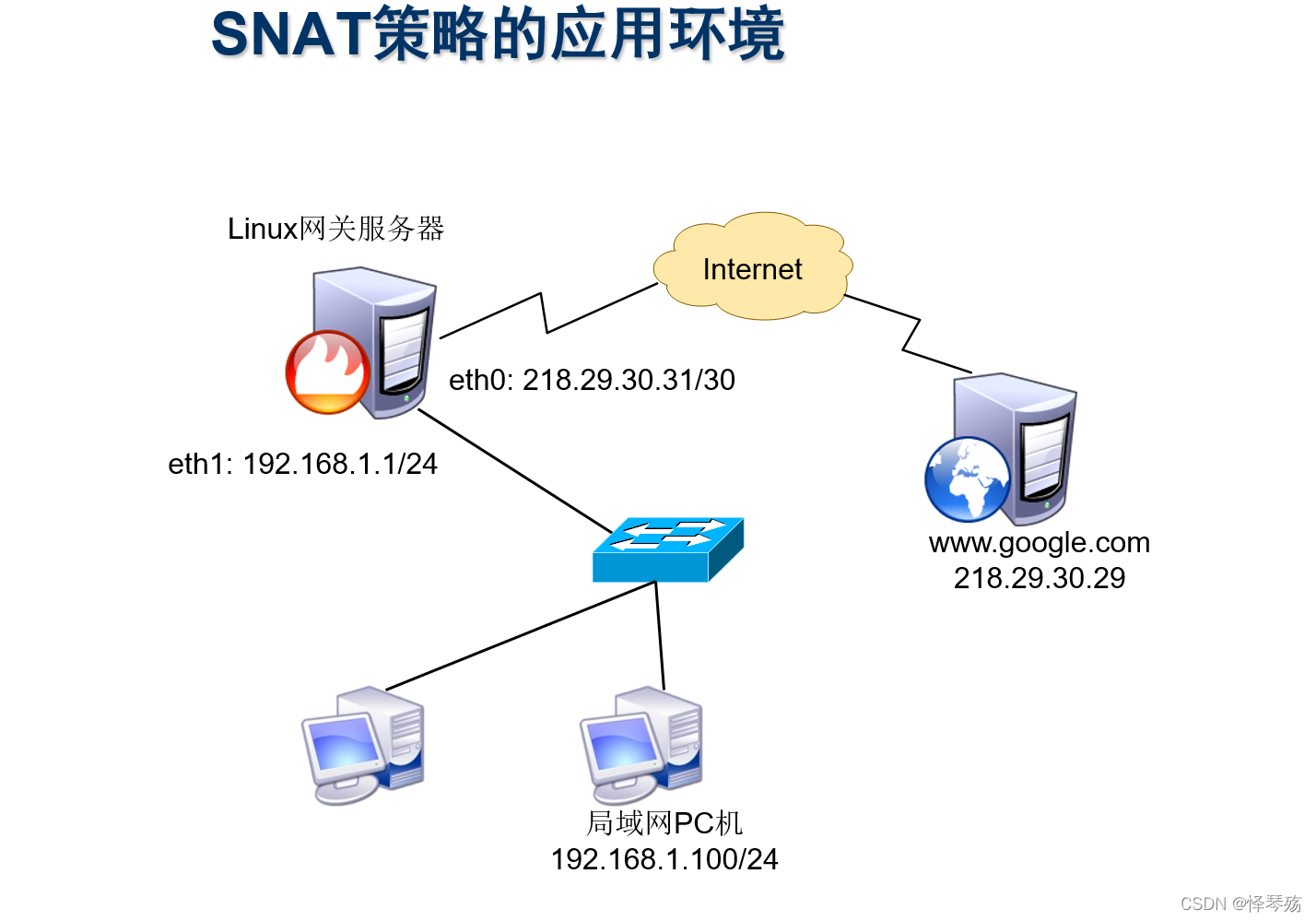
Information security - threat detection - detailed design of NAT log access threat detection platform
随机推荐
China exterior wall cladding (EWC) market trend report, technical dynamic innovation and market forecast
Raspberry pie csi/usb camera uses mjpg to realize web camera monitoring
[teacher Gao UML software modeling foundation] collection of exercises and answers for level 20 cloud class
Research Report of cylindrical grinder industry - market status analysis and development prospect forecast
Matlab comprehensive exercise: application in signal and system
渗透测试 ( 5 ) --- 扫描之王 nmap、渗透测试工具实战技巧合集
[exercise-6] (PTA) divide and conquer
洛谷P1102 A-B数对(二分,map,双指针)
Essai de pénétration (1) - - outils nécessaires, navigation
Penetration test (7) -- vulnerability scanning tool Nessus
Find 3-friendly Integers
Opencv learning log 30 -- histogram equalization
渗透测试 ( 8 ) --- Burp Suite Pro 官方文档
Perform general operations on iptables
Interval sum ----- discretization
Opencv learning log 28 -- detect the red cup cover
Opencv learning log 18 Canny operator
[analysis of teacher Gao's software needs] collection of exercises and answers for level 20 cloud class
Ball Dropping
Opencv learning log 15 count the number of solder joints and output