当前位置:网站首页>【练习-7】(Uva 10976)Fractions Again?!(分数拆分)
【练习-7】(Uva 10976)Fractions Again?!(分数拆分)
2022-07-06 09:26:00 【火焰车】
翻译:
输入正整数k,找到所有的正整数x≥y,使得
1 k = 1 x + 1 y \frac{1}{k}=\frac{1}{x}+\frac{1}{y} k1=x1+y1
这个题也是很有意思,搞一些提前的运算:
既然要求找出所有的x,y,枚举的对象自然也就是x,y了。可问题在于,枚举的范围如何?从1/12=1/156+1/13可以看出,x可以比y大很多。难道要无休止地枚举下去?当然不是。由于x≥y,有1/x ≤1/y,因此 1/k - 1/y ≤ 1/y,即 y≤2k。这样只需要在[k+1,2k]范围内枚举y,然后根据y尝试计算出x即可。
(内容来自紫书)
这也太好了!
AC代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;
const ll mod = 1e9+7;
int main()
{
int n;
while(cin>>n && n)
{
int cnt = 0;
for(int i=n+1;i<=2*n;i++)
if((i*n)%(i-n)==0)
cnt++;
cout<<cnt<<endl;
for(int i=n+1;i<=2*n;i++)
if((i*n)%(i-n)==0)
printf("1/%d = 1/%d + 1/%d\n",n,(i*n)/(i-n),i);
}
}
直接写两遍一边算cnt一边输出是因为我太懒了。。。可能有简单的方法??额应该差不多吧。
中间的判断思路是这样的:1/k = 1/x +1/y,也就是说 1/k - 1/y = 1/x就是满足条件的。
等式左边化简一下就是 y/ky - k/ky ==》 (y-k)/yk 也就是说只要这个式子能化简成 1/?就是满足条件的。
也就是 1/(yk/(y-k))的分母是个整数。也就是yk%(y-k) ==0
因此得到了代码中的那个算式。
总结:
这样算式的题,要用未知数来推出几个新的算式简化题目。
主要就是推式子,推不出来就完犊子了。。。
边栏推荐
- csapp shell lab
- Accounting regulations and professional ethics [4]
- ucorelab3
- 信息安全-威胁检测引擎-常见规则引擎底座性能比较
- 0-1 knapsack problem (I)
- JS --- all knowledge of JS objects and built-in objects (III)
- JS --- BOM details of JS (V)
- C语言学习笔记
- China's earthwork equipment market trend report, technical dynamic innovation and market forecast
- Ball Dropping
猜你喜欢
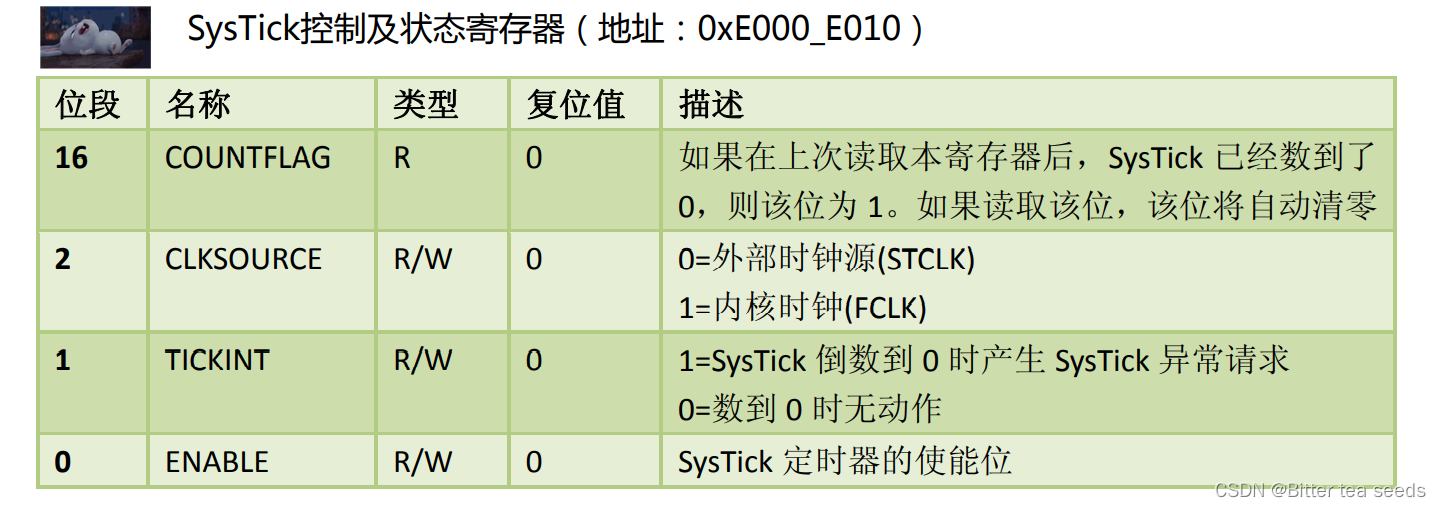
学习记录:理解 SysTick系统定时器,编写延时函数
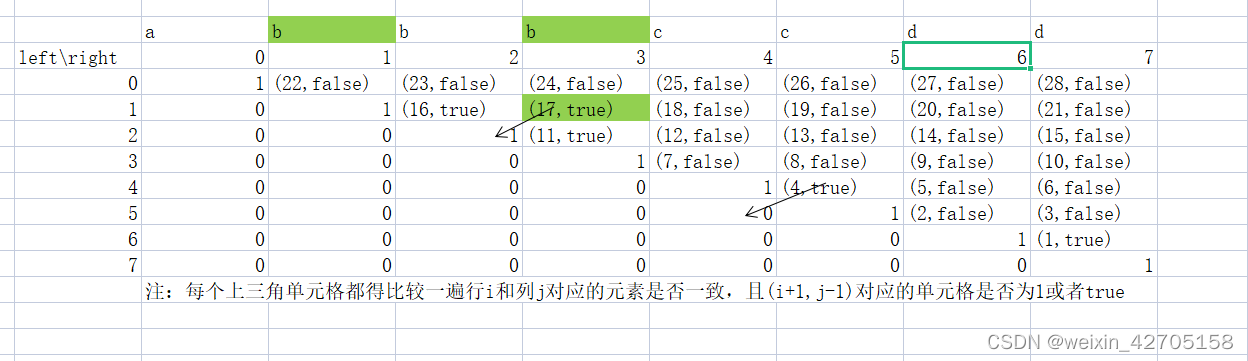
Record of force deduction and question brushing
7-1 懂的都懂 (20 分)
JS --- detailed explanation of JS facing objects (VI)

C语言是低级和高级的分水岭
Matlab comprehensive exercise: application in signal and system
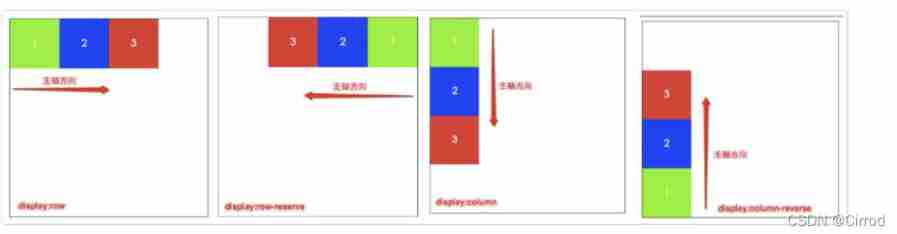
Flex --- detailed explanation of flex layout attributes
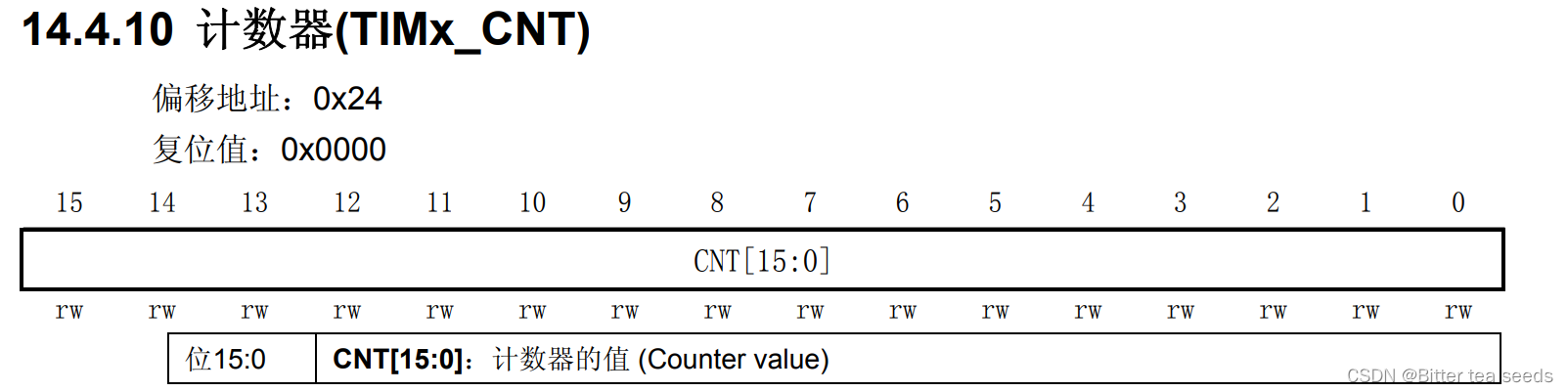
Learning record: Tim - Basic timer
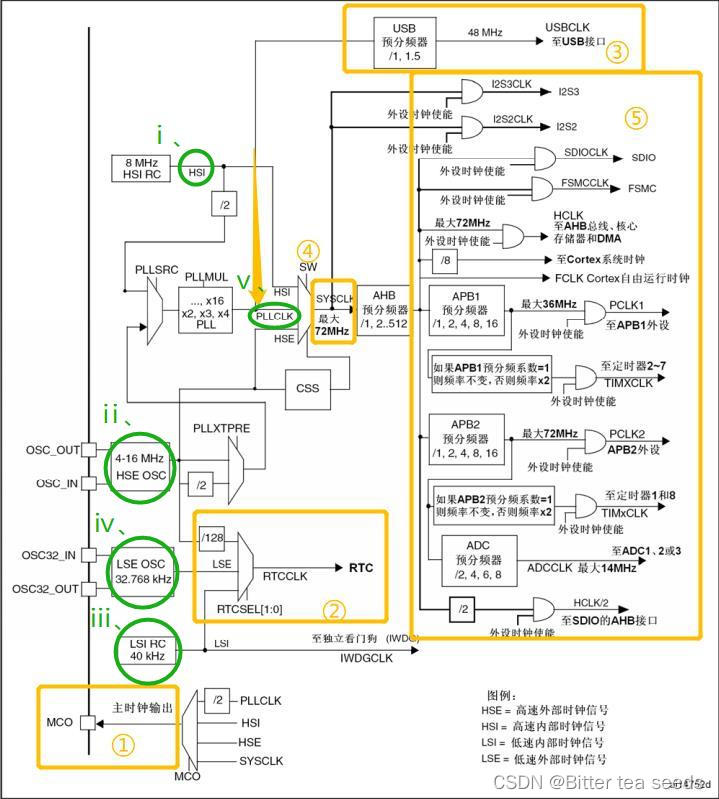
学习记录:STM32F103 时钟系统概述工作原理
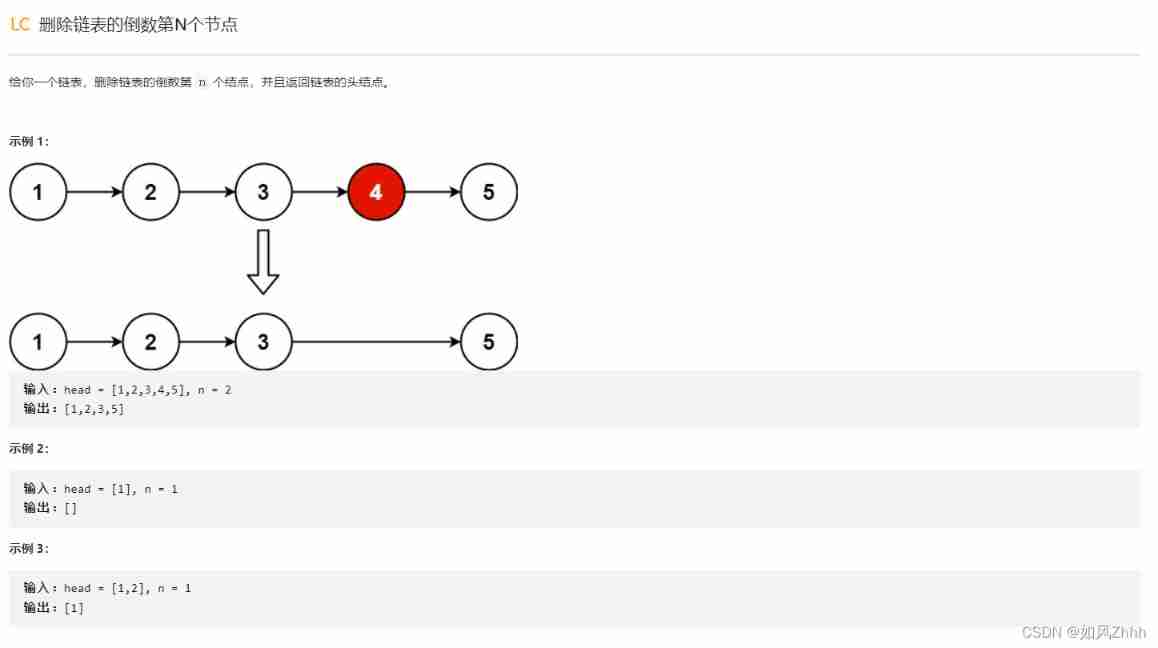
LeetCode#19. Delete the penultimate node of the linked list
随机推荐
China exterior wall cladding (EWC) market trend report, technical dynamic innovation and market forecast
SSM框架常用配置文件
Research Report on market supply and demand and strategy of Chinese graphic screen printing equipment industry
csapp shell lab
0-1背包問題(一)
E. Breaking the Wall
学习记录:STM32F103 时钟系统概述工作原理
信息安全-威胁检测引擎-常见规则引擎底座性能比较
Learning record: use STM32 external input interrupt
Cost accounting [18]
UCORE Lab 1 system software startup process
C语言必背代码大全
Learning record: STM32F103 clock system overview working principle
JS调用摄像头
C语言数组的概念
通俗地理解什么是编程语言
Cost accounting [13]
Interesting drink
Research Report on market supply and demand and strategy of China's medical chair industry
STM32学习记录:输入捕获应用