当前位置:网站首页>0 - 1 problème de sac à dos (1)
0 - 1 problème de sac à dos (1)
2022-07-06 15:38:00 【Petit Geng qui aime apprendre】
Catalogue des articles de la série
0-1Problème de sac à dos(Un.)
Conseils:Après avoir écrit l'article,Le répertoire peut être généré automatiquement,Comment générer un document d'aide à droite
Catalogue des articles
Préface
Conseils:Voici le texte de cet article,Les exemples suivants sont à titre de référence
Un.、0-1Quel est le problème avec le sac à dos??
Le problème avec le sac à dos est「Planification dynamique」Une catégorie très classique de problèmes,Le problème du sac à dos appartient essentiellement à l'optimisation combinatoire「NP Question complète」.Parce qu'il y a trop de combinaisons,Il n'est donc pas possible de résoudre le problème par la méthode de l'épuisement,C'est pour ça que「Problème de sac à dos」Sera utilisé「Planification dynamique」Pour résoudre les causes profondes.Voici un exemple simple0-1Problème de sac à dos.
2.、Diviser l'égalité et le Sous - ensemble(Leetcode 416Moyenne)
1.Description du problème
Pour toi Ne contient que des entiers positifs De Non vide Tableau nums .Décidez si vous pouvez diviser le tableau en deux sous - ensembles,Rendre les éléments des deux sous - ensembles égaux.
2.Aperçu de l'algorithme
2.1 0-1L'idée de base du problème du sac à dos
0-1 Le problème du sac à dos est essentiellement un problème de programmation dynamique , L'essence du problème de programmation dynamique est de rechercher les changements numériques causés par les changements dans l'état suivant et l'état précédent ,C'est - à - dire l'équation de transfert d'état,dp[i][j]Etdp[i-1][j]La relation entre.
0-1 Le problème du sac à dos est en fait le même problème ,dp[i][j]=max(dp[i-1][j],dp[i-1][jv[i]]+wight[i]), Ça veut dire traverser un objet à la fois , Il y a deux options :Prendre ou ne pas prendre, Le volume du sac à dos sera réduit , .Si vous ne récupérez pas, gardez l'état original .
2.2 Analyse des problèmes spécifiques
Cette question peut être convertie en question de sac à dos , Processus de modélisation des problèmes : Quelle est la taille du sac à dos 、 Quantité et valeur des articles 、 Forme des résultats
1.Nombre d'articles:numsDesize
2.Valeur de l'article:numsLa valeur correspondante
3. Le volume du sac à dos : C'est le point difficile de la forme générale du sac à dos , Il n'y a aucune indication sur la valeur maximale du sac à dos , Il faut déformer le problème : Rendre les éléments des deux sous - ensembles égaux ==》 Somme de chaque sous - ensemble == Tous les éléments et 1/2, Donc le volume du sac à dos est aussi évident que tous les éléments et 1/2.
4. Forme des résultats : Il faut d'abord analyser ce que nous avons calculé , Calculer la valeur obtenue comme étant la valeur maximale qui peut être obtenue comme étant le volume du sac à dos , La question est de savoir si c'est égal. , La forme du résultat peut donc être convertie en : Le sac à dos peut - il être rempli , C'est - à - dire si la valeur maximale est égale au volume du sac à dos .
Cet article ne présente que la solution la plus primitive au problème du sac à dos , C'est aussi la forme originale , .Plusieurs variantes et Optimisations sont faites autour de ce sujet dans les prochains articles
2.4 Affichage du Code:
class Solution {
public:
bool canPartition(vector<int>& nums) {
int N=nums.size();
int sum=0;
for(int i=0;i<N;i++)
{
sum+=nums[i];
}
if(sum%2!=0) return false;
int C=sum/2;
vector<vector<int>>dp(N,vector<int>(C+1,0));
// D'abord.「 Considérez le premier article 」Situation
for (int i = 0; i <= C; i++) {
dp[0][i] = i>=nums[0] ? nums[0] : 0;
}
// Retraitement「 Considérez le reste 」Situation
for (int i = 1; i < N; i++) {
for (int j = 0; j < C + 1; j++) {
// Ne choisissez pas cet article
int n = dp[i - 1][j];
// Sélectionnez cet article ,Prémisse「Capacité restante」Supérieur ou égal à「Volume de l'article」
int y =j>nums[i]? dp[i - 1][j-nums[i]]+nums[i]:0;
dp[i][j] =max(n,y);
}
}
return dp[N-1][C]==C;
}
};
Résumé
Conseils:Voici un résumé de l'article:
Aujourd'hui, l'explication principale「Qu'est - ce qu'un problème de sac à dos」、「 Quelle est la nature du problème du sac à dos 」Et「 Pourquoi la programmation dynamique est - elle nécessaire pour résoudre le problème du sac à dos et la difficulté de résoudre les problèmes de routine et de déformation du sac à dos ,Parmi eux「01Sac à dos」 Le problème est au cœur des nombreux problèmes de sac à dos .
边栏推荐
- Learning record: use STM32 external input interrupt
- csapp shell lab
- Eslint--- error: newline required at end of file but not found (EOL last) solution
- Cost accounting [24]
- Cost accounting [14]
- Cost accounting [16]
- JDBC introduction
- Mysql database (II) DML data operation statements and basic DQL statements
- Cost accounting [13]
- Collection collection and map collection
猜你喜欢

ucorelab4
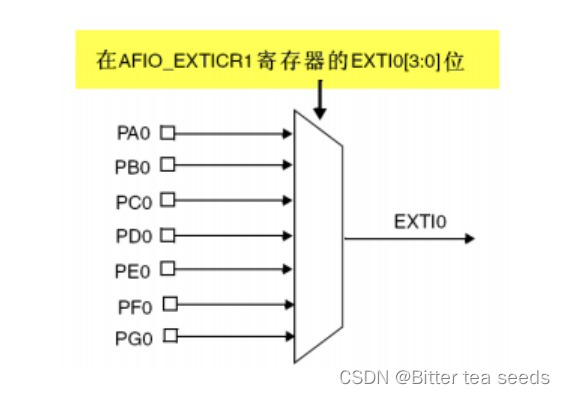
Learning record: use STM32 external input interrupt
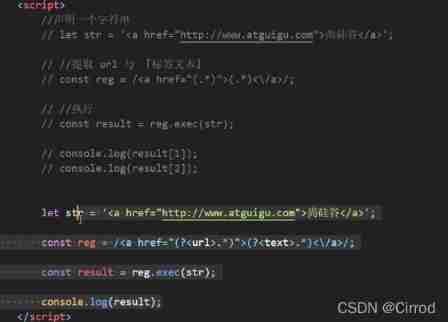
Es6---es6 content details
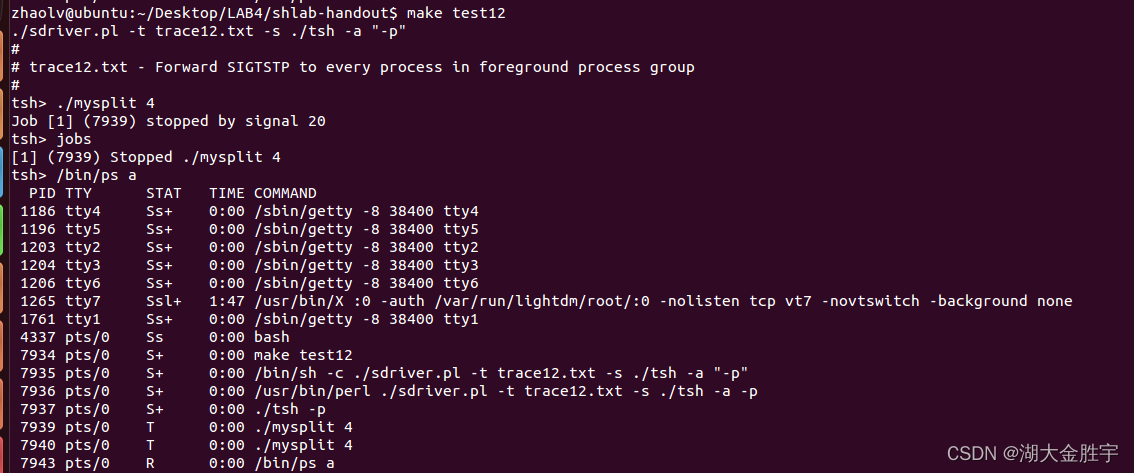
csapp shell lab
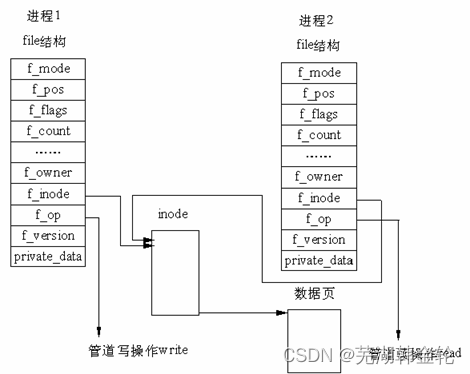
Lab 8 文件系统
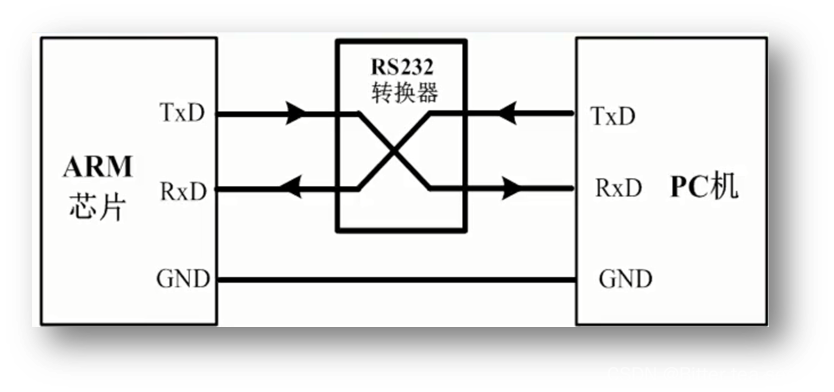
Learning records: serial communication and solutions to errors encountered
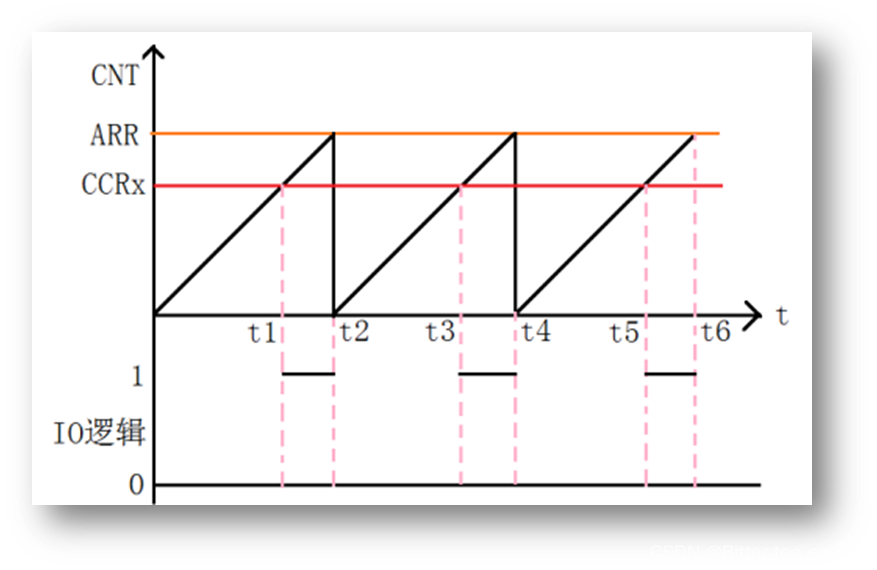
学习记录:如何进行PWM 输出
![Unpleasant error typeerror: cannot perform 'ROR_‘ with a dtyped [float64] array and scalar of type [bool]](/img/dc/834463f460c085207dc9d531805e90.jpg)
Unpleasant error typeerror: cannot perform 'ROR_‘ with a dtyped [float64] array and scalar of type [bool]
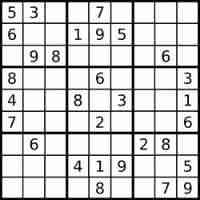
LeetCode#36. Effective Sudoku
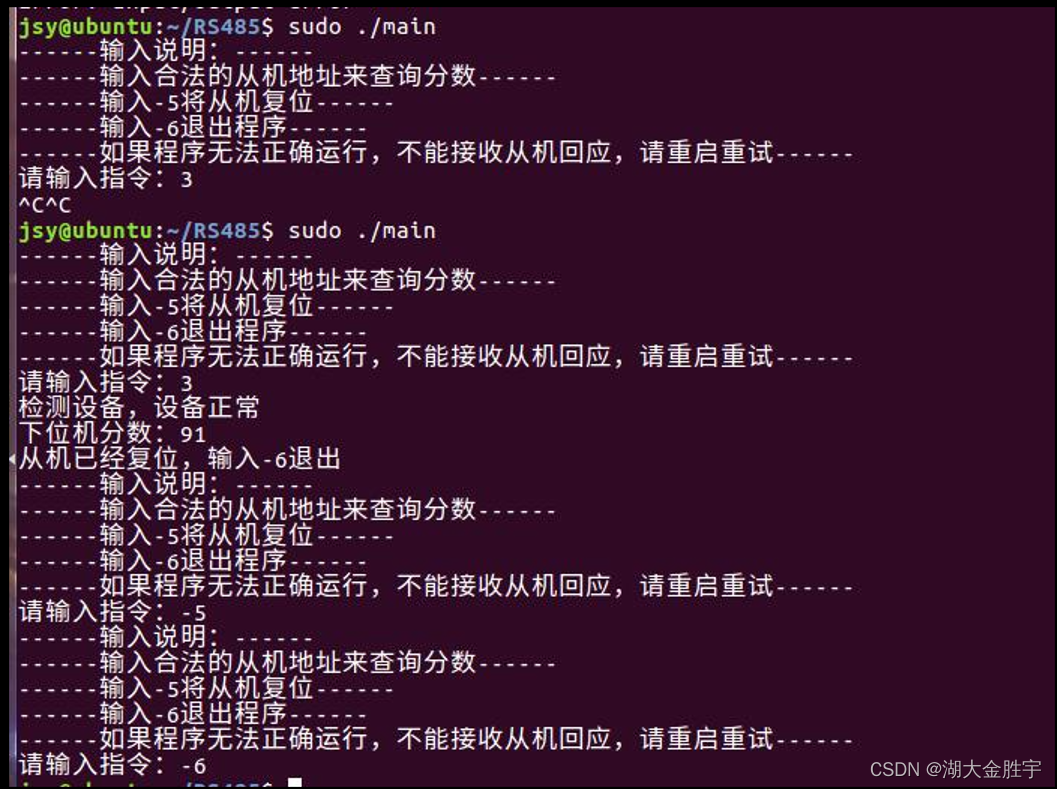
Scoring system based on 485 bus
随机推荐
Mysql database (V) views, stored procedures and triggers
Research Report on medical toilet industry - market status analysis and development prospect forecast
What to do when programmers don't modify bugs? I teach you
How to write the bug report of software test?
What if software testing is too busy to study?
JS --- JS function and scope (II)
ucore lab5
MySQL transactions
ucorelab4
JS --- detailed explanation of JS facing objects (VI)
Accounting regulations and professional ethics [4]
Research Report on market supply and demand and strategy of Chinese hospital cleaning chemicals industry
学习记录:如何进行PWM 输出
How to become a good software tester? A secret that most people don't know
Perinatal Software Industry Research Report - market status analysis and development prospect forecast
Do you know the performance testing terms to be asked in the software testing interview?
学习记录:使用STM32外部输入中断
LeetCode#237. Delete nodes in the linked list
STM32如何使用STLINK下载程序:点亮LED跑马灯(库版本)
力扣刷题记录--完全背包问题(一)