当前位置:网站首页>LeetCode#36. Effective Sudoku
LeetCode#36. Effective Sudoku
2022-07-06 15:21:00 【Rufeng ZHHH】
subject :
Please judge a 9 x 9 Is the Sudoku effective . It only needs According to the following rules , Verify that the numbers you have filled are valid .
Numbers 1-9 Only once in a row .
Numbers 1-9 It can only appear once in each column .
Numbers 1-9 Separated by thick solid lines in each 3x3 Only once in the palace .( Please refer to the example figure )
Be careful :
An effective Sudoku ( Part has been filled in ) Not necessarily solvable .
Just follow the above rules , Verify that the numbers you have filled are valid .
Blank space '.' Express .
Example 1:

Input :board =
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output :true
Example 2:
Input :board =
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
Output :false
explain : Except for the first number in the first line from 5 Change it to 8 outside , The other numbers in the space are the same as Example 1 identical . But because of the 3x3 There are two in the palace 8 There is , So this Sudoku is invalid .
Tips :
board.length == 9
board[i].length == 9
board[i][j] It's a number (1-9) perhaps '.'
source : Power button (LeetCode)
link : Power button
Personally, I think this problem is mainly about the third condition of Sudoku judgment, which is relatively difficult , The first two conditions should be able to understand the principle by looking at the code , We mainly talk about the judgment process of the third condition .
Let's create a string first , The following methods will be used .
store="0123456789"Conditions for a :
for i in board:
for j in store:
num=i.count(j)
if num>1:
return FalseCondition 2 :
nums=0
while nums < 9:
ls=[]
for i in board:
ls.append(i[nums])
for j in store:
if ls.count(j)>1:
return False
nums+=1Condition 3 :
We know that every Sudoku matrix has 9 A small cube matrix , So we can think of a way , Judge whether a small cube matrix is qualified each time , In this case, we have to judge 9 Time ( This is the cycle 9 Time ).
Subdivide again , Every three small square matrices are in one row , So we can judge three times in each line ( loop 3 Time ).
Through this , With the help of method 2 ( Create another list ) Same method , We can judge whether each of our small squares is qualified .
Here it is , I created two variables to help with the loop ,line: Indicates the number of rows indexed ; lis: Indicates the number of columns in the index .
line=0;lis=0;ll=[]
for i in range(3): # Circle the three lines ( One big line corresponds to three small lines )
for i in range(3): # Every big line ( Three small lines ), Cycle three times ,3 ride 3 be equal to 9
for j in board[line:line+3]:
for k in j[lis:lis+3]:
ll.append(k)
for m in store:
if ll.count(m)>1:
return False
lis+=3 # Advance the number of columns by three , Enter the next cube matrix of the big row
ll=[] # Notice that after judging each small cube matrix , Clear list
lis=0 # After a large line of each cycle , Zero the number of columns
line+=3 # Go a long way Last , If the above judgment does not return False, Then this is an effective Sudoku , We return at the end True that will do .
class Solution:
def isValidSudoku(self, board: List[List[str]]) -> bool:
store="123456789"
for i in board:
for j in store:
num=i.count(j)
if num>1:
return False
nums=0
while nums < 9:
ls=[]
for i in board:
ls.append(i[nums])
for j in store:
if ls.count(j)>1:
return False
nums+=1
line=0;lis=0;ll=[]
for i in range(3):
for i in range(3):
for j in board[line:line+3]:
for k in j[lis:lis+3]:
ll.append(k)
for m in store:
if ll.count(m)>1:
return False
lis+=3
ll=[]
lis=0
line+=3
return True
边栏推荐
- The minimum number of operations to convert strings in leetcode simple problem
- ucore lab7
- Thinking about three cups of tea
- 软件测试有哪些常用的SQL语句?
- UCORE lab2 physical memory management experiment report
- What is "test paper test" in software testing requirements analysis
- JDBC介绍
- Dlib detects blink times based on video stream
- 软件测试行业的未来趋势及规划
- UCORE lab8 file system experiment report
猜你喜欢
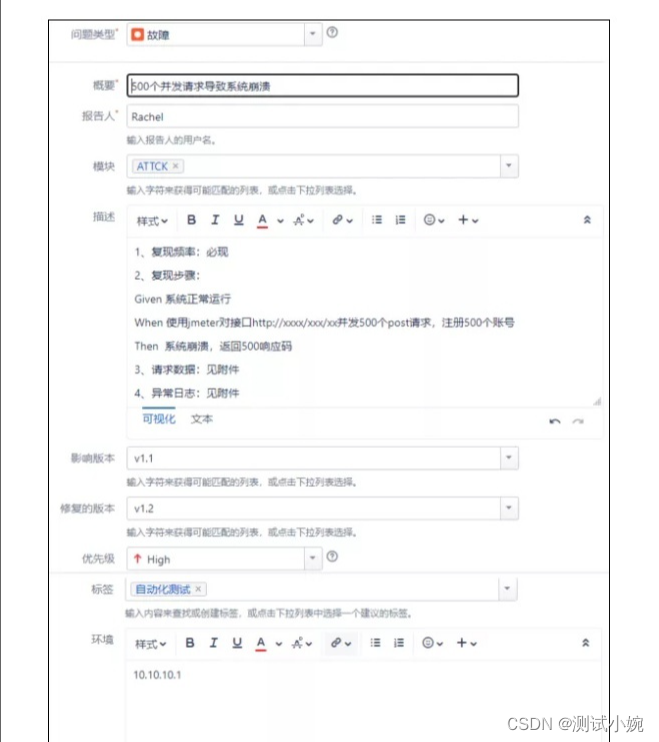
How to write the bug report of software test?
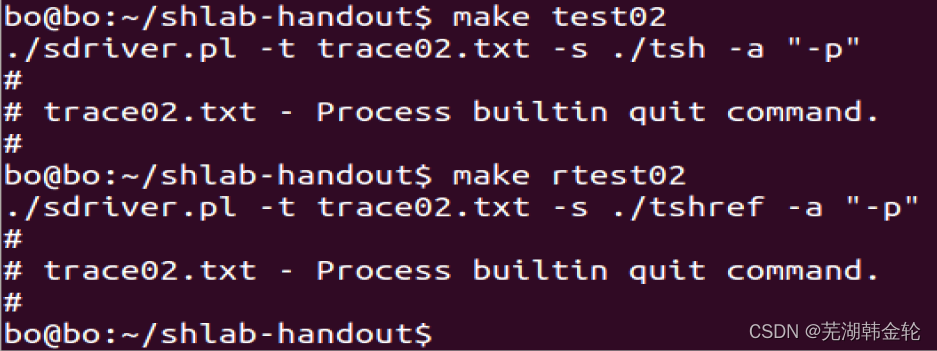
CSAPP shell lab experiment report
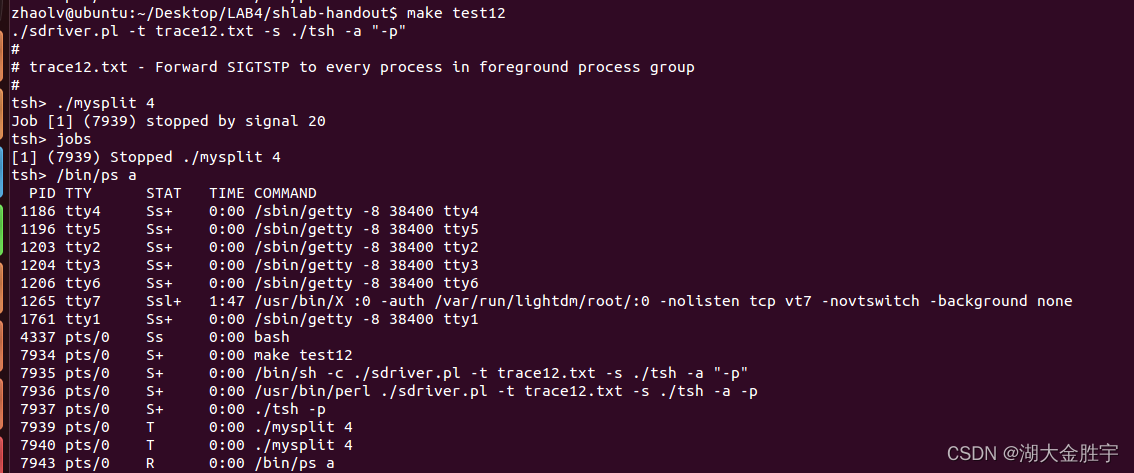
csapp shell lab
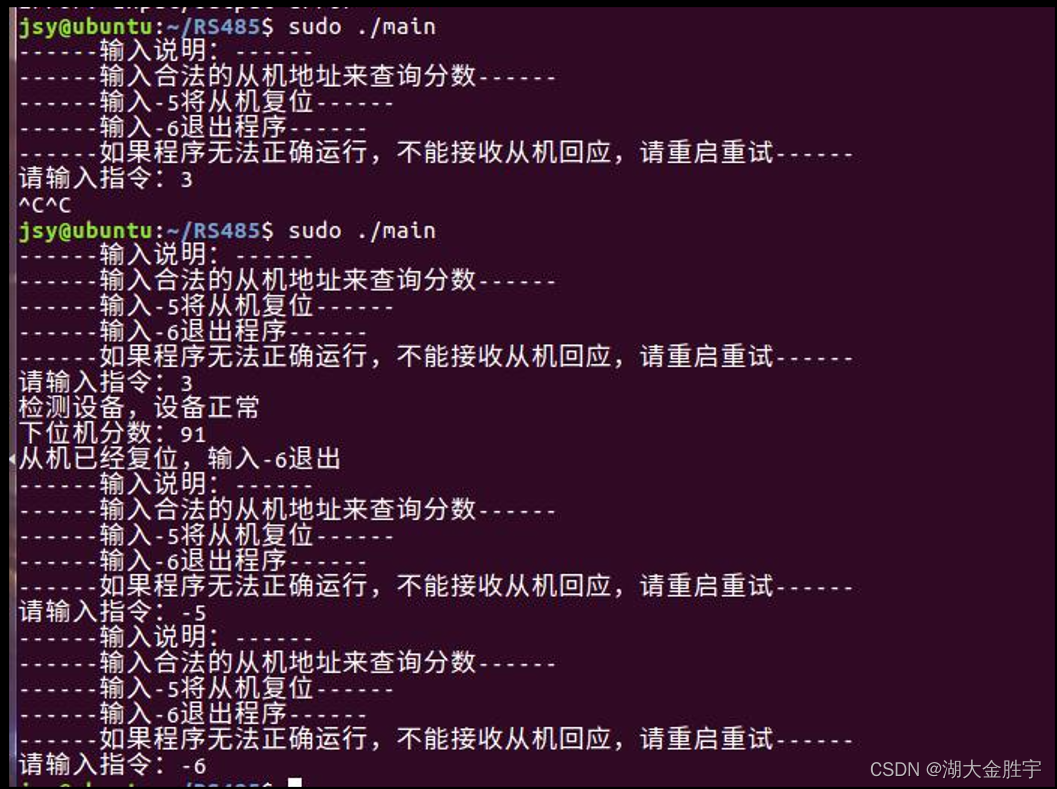
Scoring system based on 485 bus
What to do when programmers don't modify bugs? I teach you

Sorting odd and even subscripts respectively for leetcode simple problem
Stc-b learning board buzzer plays music 2.0
ucore lab5

Pedestrian re identification (Reid) - Overview
软件测试行业的未来趋势及规划
随机推荐
Dlib detects blink times based on video stream
Install and run tensorflow object detection API video object recognition system of Google open source
Capitalize the title of leetcode simple question
UCORE lab5 user process management experiment report
[pytorch] simple use of interpolate
Threads et pools de threads
Stc-b learning board buzzer plays music 2.0
Réponses aux devoirs du csapp 7 8 9
Mysql database (IV) transactions and functions
Collection集合与Map集合
ucore lab 6
Jupyter installation and use tutorial
Word macro operation: convert the automatic number in the document into editable text type
What are the business processes and differences of the three basic business modes of Vos: direct dial, callback and semi direct dial?
转行软件测试必需要知道的知识
The wechat red envelope cover designed by the object is free! 16888
Heap, stack, queue
Global and Chinese markets for complex programmable logic devices 2022-2028: Research Report on technology, participants, trends, market size and share
The minimum sum of the last four digits of the split digit of leetcode simple problem
A method and implementation of using VSTO to prohibit excel cell editing

