当前位置:网站首页>力扣刷题记录--完全背包问题(一)
力扣刷题记录--完全背包问题(一)
2022-07-06 09:25:00 【爱学习的小耿】
系列文章目录
完全背包问题(一)
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
前言
提示:这里可以添加本文要记录的大概内容:
提示:以下是本篇文章正文内容,下面案例可供参考
一、完全背包问题简介
完全背包问题其实就是在 0-1 背包问题的基础上,增加了每件物品可以选择多次的特点(在容量允许的情况下)。
二、零钱兑换(Leetcode 322中等)
1.问题描述
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。你可以认为每种硬币的数量是无限的。
2.算法概述
2.1 完全背包问题问题的基本思路
完全背包问题和0-1背包问题的本质是一样的,只不过是条件不一样了。下面我根据代码来分析。下面的代码就是解决完全背包问题的一般处理方法。和0-1背包问题不同的是:在考虑当前硬币的情况时可以选择多次,选择的最大次数=当前背包余量/当前硬币的面值。
class Solution {
int INF = Integer.MAX_VALUE;
public int coinChange(int[] cs, int cnt) {
int n = cs.length;
int[][] f = new int[n + 1][cnt + 1];
// 初始化(没有任何硬币的情况):只有 f[0][0] = 0;其余情况均为无效值。
// 这是由「状态定义」决定的,当不考虑任何硬币的时候,只能凑出总和为 0 的方案,所使用的硬币数量为 0
for (int i = 1; i <= cnt; i++) f[0][i] = INF;
// 有硬币的情况
for (int i = 1; i <= n; i++) {
int val = cs[i - 1];
for (int j = 0; j <= cnt; j++) {
// 不考虑当前硬币的情况
f[i][j] = f[i - 1][j];
// 考虑当前硬币的情况(可选当前硬币个数基于当前容量大小)
for (int k = 1; k * val <= j; k++) {
if (f[i - 1][j - k * val] != INF) {
f[i][j] = Math.min(f[i][j], f[i-1][j-k*val] + k);
}
}
}
}
return f[n][cnt] == INF ? -1 : f[n][cnt];
}
}
2.2 具体问题分析
此题可以转换为完全背包问题,问题建模过程:背包的容积有多大、物品的数量和价值、结果形式
1.物品的数量:nums的size
2.物品的价值:nums对应的数值
3.背包的容积:背包的大小
4.初始值:这一点也是很多背包问题的难点,这里所谓初始值,无非就是dp[0]、dp[1]…dp[n]代表的含义。想要确定初始值就要根据题目的含义确定哪些值是无效值,哪些值才是需要去转移的值。
5.结果形式:题目的问题是如何计算并返回可以凑成总金额所需的最少的硬币个数。背包问题最原始的题解是找到价值最大的那个解。但是现在需要变通,本质上还是在分析状态转移方程。就是dp[j]和dp[j - v[i]]的关系,这里就是选了这个硬币,我最后想要的是最少的硬币数量并非最大价值,因此dp[j]和dp[j - v[i]]就是dp[j]=min(dp[j],dp[j - v[i]]+1);
6.最后的结果获得:需要根据初始值来判断哪些值是有效值,哪些是无效值。
2.4 代码展示:
class Solution {
private:
int INF = 0x3f3f3f3f;
public:
int coinChange(vector<int>& coins, int amount) {
int C=coins.size();
vector<int> dp(amount+1,INF);
dp[0]=0;
if(amount==0) return 0;
for(int i=0;i<C;i++)
{
for(int j=coins[i];j<=amount;j++)
{
int yes=dp[j-coins[i]]+1;
dp[j]=min(dp[j],yes);
}
}
return dp[amount]==INF?-1:dp[amount];
}
};
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了「什么是完全背包问题」、「背包问题的本质是什么」以及「为什么完全背包问题常规解法以及完全背包的解决套路和变形题的难点,后面会根据示例做更多的介绍。
边栏推荐
猜你喜欢
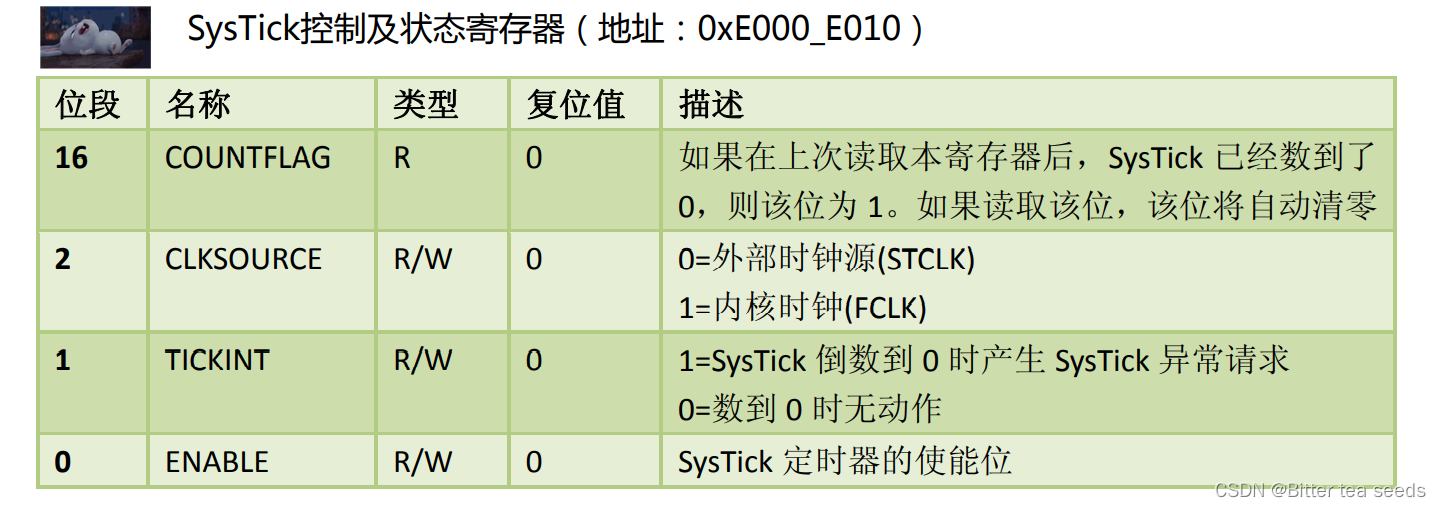
Learning record: understand systick system timer and write delay function

51 lines of code, self-made TX to MySQL software!
Mysql database (I)
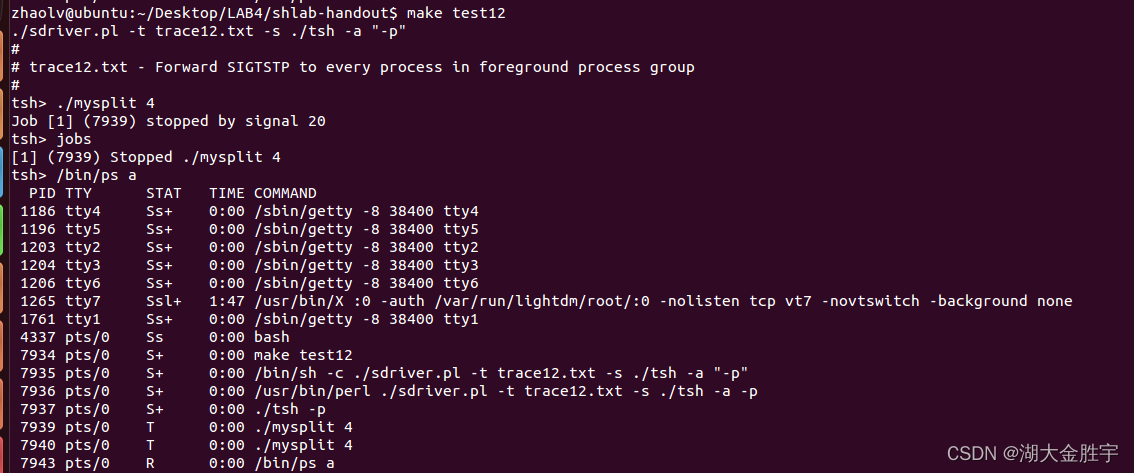
csapp shell lab
STM32 learning record: input capture application
学习记录:如何进行PWM 输出

What are the commonly used SQL statements in software testing?
遇到程序员不修改bug时怎么办?我教你
Eslint--- error: newline required at end of file but not found (EOL last) solution
How to build a nail robot that can automatically reply
随机推荐
Example 071 simulates a vending machine, designs a program of the vending machine, runs the program, prompts the user, enters the options to be selected, and prompts the selected content after the use
Knowledge that you need to know when changing to software testing
Intensive learning notes: Sutton book Chapter III exercise explanation (ex17~ex29)
LeetCode#204. Count prime
FSM and I2C experiment report
Lab 8 文件系统
软件测试需求分析之什么是“试纸测试”
Crawler series of learning while tapping (3): URL de duplication strategy and Implementation
ucore lab 2
Es6--- two methods of capturing promise status as failed
Learning record: understand systick system timer and write delay function
学习记录:TIM—电容按键检测
What are the software testing methods? Show you something different
ucore Lab 1 系统软件启动过程
How to write the bug report of software test?
ucore lab7
Learning record: STM32F103 clock system overview working principle
Heap, stack, queue
LeetCode#268. Missing numbers
全网最详细的postman接口测试教程,一篇文章满足你
