当前位置:网站首页>LeetCode#62. Different paths
LeetCode#62. Different paths
2022-07-06 15:21:00 【Rufeng ZHHH】
subject :
A robot is in a m x n The top left corner of the grid ( The starting point is marked as “Start” ).
The robot can only move down or right one step at a time . The robot tries to reach the bottom right corner of the grid ( In the figure below, it is marked as “Finish” ).
Ask how many different paths there are in total ?
Example 1:

Input :m = 3, n = 7
Output :28
Example 2:
Input :m = 3, n = 2
Output :3
explain :
From the top left corner , All in all 3 Path to the bottom right .
1. towards the right -> Down -> Down
2. Down -> Down -> towards the right
3. Down -> towards the right -> Down
Example 3:
Input :m = 7, n = 3
Output :28
Example 4:
Input :m = 3, n = 3
Output :6
Tips :
1 <= m, n <= 100
Question data guarantee that the answer is less than or equal to 2 * 109
source : Power button (LeetCode)
link :62. Different paths - Power button (LeetCode) (leetcode-cn.com)
Method 1 ( Permutation and combination ):
When I first saw this problem, I first thought of it in Mathematics Permutation and combination ( A kind of Combinatorial Mathematics )_ Baidu Encyclopedia (baidu.com), Many high school students must have done this kind of problem , The method is also relatively simple .
Let's assume that we have to go altogether m+n Step , Then just let one of them m Step right , remainder n Step must be down , The calculation is C(m+n,n)=C(m+n,m).
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
son=min(m-1,n-1);mother=m+n-2
up=1;down=1
for i in range(son):
up*=son-i
for i in range(son):
down*=mother-i
if int(down/up)==0:
return 1
else:
return int(down/up)Method 2 ( Dynamic programming ):
Let's suppose we get to the k Step , Then the general method of the previous steps is the first two k-1 Sum of steps ( From the top left to the bottom right can only be the last step, coming from the left or the top , Otherwise it will be meaningless ), It's just like this in terms of images .

So we need to create a two-dimensional list :
dp=[]
for i in range(m):
dp.append([1]*n) # The default starting values are 1After creation , It can be calculated according to this idea , This is similar to Yang Hui's Algorithm LeetCode#118. Yang hui triangle _ As the wind Zhhh The blog of -CSDN Blog
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp=[]
for i in range(m):
dp.append([1]*n)
for i in range(m-1):
for j in range(n-1):
dp[i+1][j+1]=dp[i][j+1]+dp[i+1][j]
return dp[m-1][n-1]边栏推荐
- Build your own application based on Google's open source tensorflow object detection API video object recognition system (II)
- CSAPP homework answers chapter 789
- Servlet
- Public key box
- Introduction to safety testing
- MySQL development - advanced query - take a good look at how it suits you
- The minimum sum of the last four digits of the split digit of leetcode simple problem
- ucore lab 6
- Leetcode simple question: check whether the numbers in the sentence are increasing
- 線程及線程池
猜你喜欢
![Cadence physical library lef file syntax learning [continuous update]](/img/0b/75a4ac2649508857468d9b37703a27.jpg)
Cadence physical library lef file syntax learning [continuous update]
UCORE lab1 system software startup process experimental report

接口测试面试题及参考答案,轻松拿捏面试官
How to do agile testing in automated testing?

Threads et pools de threads
Scoring system based on 485 bus
Lab 8 file system
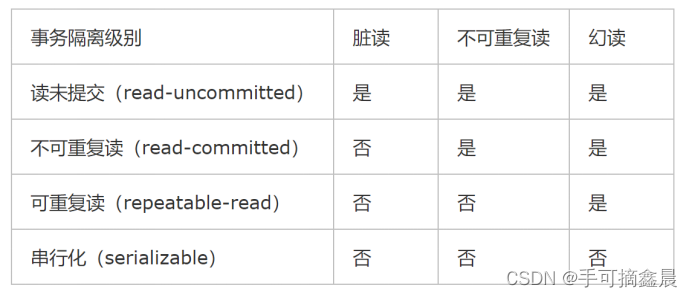
MySQL数据库(四)事务和函数
In Oracle, start with connect by prior recursive query is used to query multi-level subordinate employees.

Crawler series of learning while tapping (3): URL de duplication strategy and Implementation
随机推荐
Video scrolling subtitle addition, easy to make with this technique
Global and Chinese market of RF shielding room 2022-2028: Research Report on technology, participants, trends, market size and share
MySQL transactions
Sleep quality today 81 points
The latest query tracks the express logistics and analyzes the method of delivery timeliness
Report on the double computer experiment of scoring system based on 485 bus
ucore lab 6
Emqtt distribution cluster and node bridge construction
软件测试Bug报告怎么写?
软件测试面试回答技巧
自动化测试中敏捷测试怎么做?
Build your own application based on Google's open source tensorflow object detection API video object recognition system (II)
What if software testing is too busy to study?
ArrayList集合
遇到程序员不修改bug时怎么办?我教你
Global and Chinese market of goat milk powder 2022-2028: Research Report on technology, participants, trends, market size and share
How to become a good software tester? A secret that most people don't know
软件测试有哪些常用的SQL语句?
Dlib detects blink times based on video stream
MySQL数据库(三)高级数据查询语句
