当前位置:网站首页>Record of brushing questions with force deduction -- complete knapsack problem (I)
Record of brushing questions with force deduction -- complete knapsack problem (I)
2022-07-06 15:40:00 【Xiaogeng who loves learning】
List of articles
Complete knapsack problem ( One )
Tips : After writing the article , Directories can be generated automatically , How to generate it, please refer to the help document on the right
List of articles
Preface
Tips : Here you can add the general content to be recorded in this article :
Tips : The following is the main body of this article , The following cases can be used for reference
One 、 Introduction to the complete knapsack problem
The complete knapsack problem is actually 0-1 Based on the knapsack problem , Added feature that each item can be selected multiple times ( Where capacity permits ).
Two 、 Change for (Leetcode 322 secondary )
1. Problem description
Give you an array of integers coins , Coins of different denominations ; And an integer amount , Represents the total amount . Calculate and return the amount needed to make up the total amount The minimum number of coins . If no combination of coins can make up the total amount , return -1 . You can think of the number of coins of each kind as infinite .
2. Description of algorithm
2.1 The basic idea of the complete knapsack problem
Complete knapsack problem and 0-1 The essence of knapsack problem is the same , It's just that the conditions are different . Now I will analyze it according to the code . The following code is the general method to solve the complete knapsack problem . and 0-1 The difference between the knapsack problem is : When considering the current coin situation, you can choose multiple times , Maximum number of selections = Current backpack allowance / The face value of the current coin .
class Solution {
int INF = Integer.MAX_VALUE;
public int coinChange(int[] cs, int cnt) {
int n = cs.length;
int[][] f = new int[n + 1][cnt + 1];
// initialization ( There are no coins ): Only f[0][0] = 0; Other cases are invalid values .
// This is from 「 State definition 」 Decisive , When not considering any coins , You can only add up to 0 The plan , The number of coins used is 0
for (int i = 1; i <= cnt; i++) f[0][i] = INF;
// With coins
for (int i = 1; i <= n; i++) {
int val = cs[i - 1];
for (int j = 0; j <= cnt; j++) {
// Regardless of the current coin situation
f[i][j] = f[i - 1][j];
// Consider the current coin situation ( The current number of coins can be selected based on the current capacity )
for (int k = 1; k * val <= j; k++) {
if (f[i - 1][j - k * val] != INF) {
f[i][j] = Math.min(f[i][j], f[i-1][j-k*val] + k);
}
}
}
}
return f[n][cnt] == INF ? -1 : f[n][cnt];
}
}
2.2 Analysis of specific problems
This problem can be transformed into a complete knapsack problem , Problem modeling process : How big is the volume of the backpack 、 The quantity and value of items 、 The form of the result
1. Number of items :nums Of size
2. The value of the goods :nums The corresponding value
3. The volume of the backpack : Backpack size
4. Initial value : This is also the difficulty of many knapsack problems , The so-called initial value here , does dp[0]、dp[1]…dp[n] The meaning of representation . If you want to determine the initial value, you should determine which values are invalid according to the meaning of the topic , Which values need to be transferred .
5. The form of the result : The problem of the topic is how to calculate and return the minimum number of coins needed to make up the total amount . The original solution of knapsack problem is to find the solution with the greatest value . But now we need to be flexible , In essence, it is still analyzing the state transition equation . Namely dp[j] and dp[j - v[i]] The relationship between , Here is the coin , The last thing I want is that the minimum number of coins is not the maximum value , therefore dp[j] and dp[j - v[i]] Namely dp[j]=min(dp[j],dp[j - v[i]]+1);
6. The final result is : You need to judge which values are valid values according to the initial values , Which are invalid values .
2.4 Code display :
class Solution {
private:
int INF = 0x3f3f3f3f;
public:
int coinChange(vector<int>& coins, int amount) {
int C=coins.size();
vector<int> dp(amount+1,INF);
dp[0]=0;
if(amount==0) return 0;
for(int i=0;i<C;i++)
{
for(int j=coins[i];j<=amount;j++)
{
int yes=dp[j-coins[i]]+1;
dp[j]=min(dp[j],yes);
}
}
return dp[amount]==INF?-1:dp[amount];
}
};
summary
Tips : Here is a summary of the article :
for example : That's what we're going to talk about today , This article only briefly introduces 「 What is the complete knapsack problem 」、「 What is the essence of the knapsack problem 」 as well as 「 Why is the conventional solution of complete knapsack problem and the difficulty of solving routine and deformation problems of complete knapsack , More will be introduced later according to the examples .
边栏推荐
- Learning record: understand systick system timer and write delay function
- Jupyter installation and use tutorial
- LeetCode#237. Delete nodes in the linked list
- 毕业才知道IT专业大学生毕业前必做的1010件事
- China's salt water membrane market trend report, technological innovation and market forecast
- 学习记录:STM32F103 时钟系统概述工作原理
- Stm32 dossiers d'apprentissage: saisie des applications
- Intensive learning notes: Sutton book Chapter III exercise explanation (ex17~ex29)
- 学习记录:USART—串口通讯
- ucore Lab 1 系统软件启动过程
猜你喜欢
csapp shell lab
JS --- detailed explanation of JS facing objects (VI)
Intensive learning notes: Sutton book Chapter III exercise explanation (ex17~ex29)

How to become a good software tester? A secret that most people don't know
LeetCode#62. Different paths
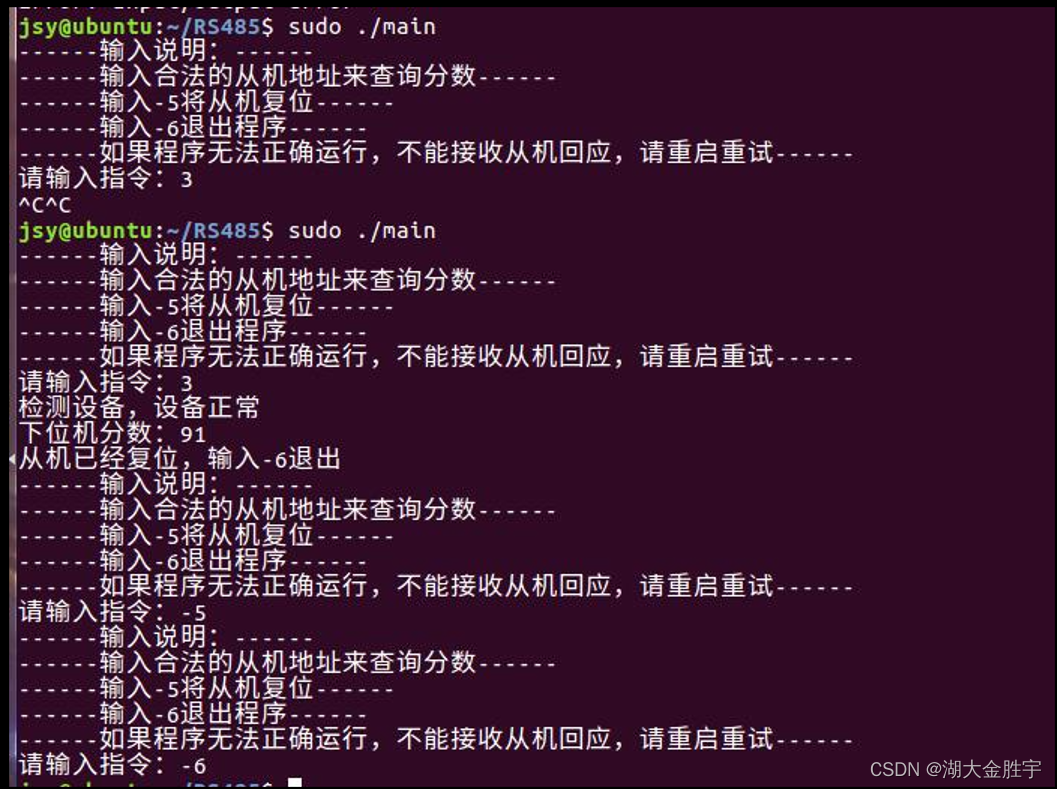
Scoring system based on 485 bus
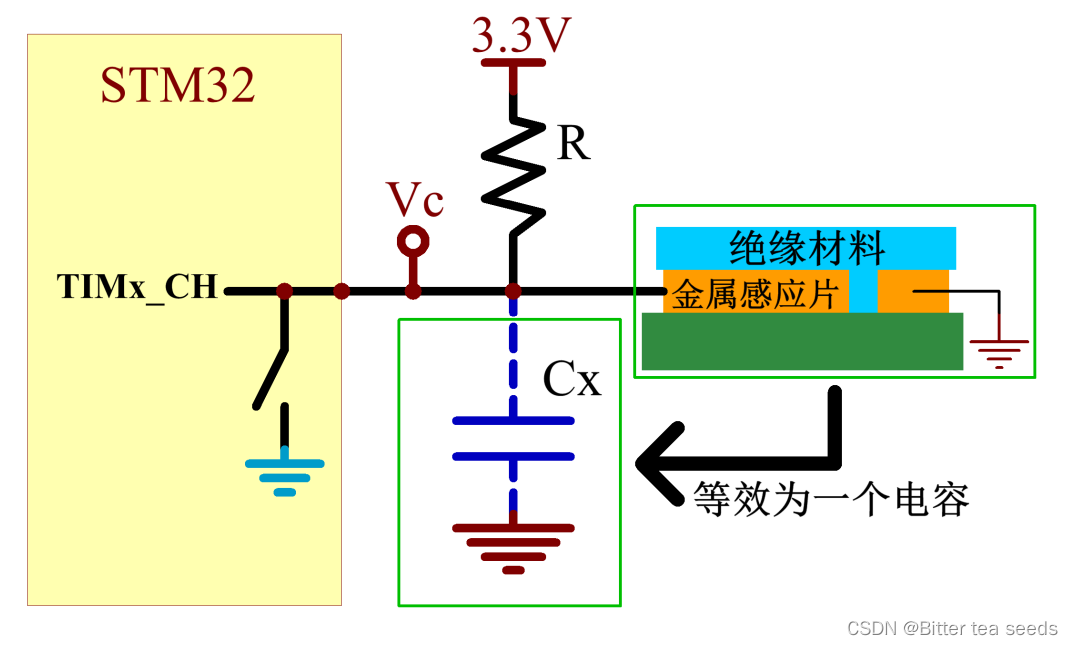
Learning record: Tim - capacitive key detection
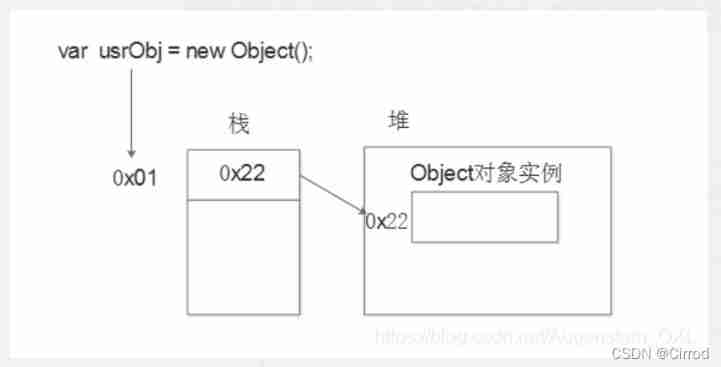
JS --- all knowledge of JS objects and built-in objects (III)
ucore lab 6
The most detailed postman interface test tutorial in the whole network. An article meets your needs
随机推荐
ucore lab7
ucore lab7
Do you know the performance testing terms to be asked in the software testing interview?
Accounting regulations and professional ethics [5]
基于485总线的评分系统
Cost accounting [21]
C4D quick start tutorial - creating models
Learning record: Tim - capacitive key detection
JS --- detailed explanation of JS DOM (IV)
Word macro operation: convert the automatic number in the document into editable text type
JS --- all basic knowledge of JS (I)
China chart recorder market trend report, technology dynamic innovation and market forecast
0-1背包问题(一)
Scoring system based on 485 bus
How to build a nail robot that can automatically reply
Leetcode notes - dynamic planning -day6
Interview answering skills for software testing
51 lines of code, self-made TX to MySQL software!
ucorelab3
TCP的三次握手与四次挥手