当前位置:网站首页>动态规划前路径问题
动态规划前路径问题
2022-07-06 09:25:00 【爱学习的小耿】
动态规划前路径问题
路径问题:本章只讲不同路径(Leecode 62)、不同路径(Leecode 63)、路径和问题(Leedcode 64)
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
前言
路径问题作为经典动态规划问题背包问题的前传,用于理解dp动态规划的思想模型。
一、不同路径问题(Leecode 62 中等)
1.问题描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下(在下图中标记为 “Finish” )。问总共有多少条不同的路径?
2.问题分析
其实动态问题只要考虑如何定义数据结构、结构的含义、状态转移方程的建立。
2.1 定义数据结构
问题是有多少不同的路径,此时应当使用dp[m-1][n-1]来表达最终的结果,上个博客里的例子是最长回文字符串,就是dp[i][j]来表达从i到j的字符串,leedcode 678的最长递增子序列就可以用dp[i]来表达,因为是连续的。
2.2 结构含义的解读
本问题中dp[i][j]就可以解读为:i代表地图的行,j代表列
最长回文字符串里的dp[i][j]:i是回文字符串的起点idx,j是回文字符串的终点
最长递增子序列:dp[i]是子序列的终点idx,由于起点是上个循环的终点,所以不需要定义为二维数组,定义为二维数组去遍历会超过时间限制,时耗太长
2.3 状态转移方程的建立
本问题中:
由于题目限定了我们只能往下或者往右 移动,因此我们按照「当前可选方向」进行分析:
当前位置只能 「往下」 移动,即有 dp[i][j] = dp[i-1][j]
当前位置只能 「往右」 移动,即有 dp[i][j] = dp[i][j-1]
当前位置即能 「往下」 也能 「往右」 移动,即有 dp[i][j] =dp[i][j-1] + dp[i-1][j]
推导过程:
dp[i][j]代表的是到达地图grid[i][j]点到达路径的条数,那么往上递推一步:如何到达grid[i][j]点,只有两种方法:由前面的点往下或者往右进入到这个点,因此到达grid[i][j]的方式就只有到达dp[i][j-1]的方式+ 到达dp[i-1][j]的方式,由此可推导出dp[i][j]的状态转移方程:dp[i][j] =dp[i][j-1] + dp[i-1][j]
3.代码展示:
代码如下(示例):
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n));
dp[0][0]=1;
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(i>0&&j>0)
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
else if(i>0)
{
dp[i][j]=dp[i-1][j];
}
else if(j>0){
dp[i][j]=dp[i][j-1];
}
}
}
return dp[m-1][n-1];
}
};
二、不同路径问题ll(Leecode 63 中等)
1.问题描述
这是 LeetCode 上的「63. 不同路径 II」,难度为 Medium。
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?网格中的障碍物和空位置分别用 1 和 0 来表示。
2.问题分析
其实动态问题只要考虑如何定义数据结构、结构的含义、状态转移方程的建立。
2.1 定义数据结构
问题是有多少不同的路径,此时应当使用dp[m-1][n-1]来表达最终的结果
2.2 结构含义的解读
本问题中dp[i][j]就可以解读为:i代表地图的行,j代表列
2.3 状态转移方程的建立
本问题中:
由于题目限定了我们只能往下或者往右 移动,因此我们按照「当前可选方向」进行分析:
当前位置只能 「往下」 移动,即有 dp[i][j] = dp[i-1][j]
当前位置只能 「往右」 移动,即有 dp[i][j] = dp[i][j-1]
当前位置即能 「往下」 也能 「往右」 移动,即有 dp[i][j] =dp[i][j-1] + dp[i-1][j]
推导过程:
dp[i][j]代表的是到达地图grid[i][j]点到达路径的条数,那么往上递推一步:如何到达grid[i][j]点,只有两种方法:由前面的点往下或者往右进入到这个点,因此到达grid[i][j]的方式就只有到达dp[i][j-1]的方式+ 到达dp[i-1][j]的方式,当然此问题遇上个问题的区别在于:上个点是否能够左移或者右移,由此可推导出dp[i][j]的状态转移方程:dp[i][j] =dp[i][j-1] + dp[i-1][j],状态方程不变,但是条件得控制:i>0&&j>0&&obstacleGrid[i-1][j]==0&&obstacleGrid[i][j-1]==0
3.代码展示:
代码如下(示例):
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int n=obstacleGrid[0].size();
int m=obstacleGrid.size();
vector<vector<int>> dp(m, vector<int>(n));
dp[0][0]=1;
if(obstacleGrid[m-1][n-1]==1)
{
return 0;
}
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(i>0&&j>0&&obstacleGrid[i-1][j]==0&&obstacleGrid[i][j-1]==0)
{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
else if(i>0&&obstacleGrid[i-1][j]==0)
{
dp[i][j]=dp[i-1][j];
}
else if(j>0&&obstacleGrid[i][j-1]==0){
dp[i][j]=dp[i][j-1];
}
}
}
return dp[m-1][n-1];
}
};
二、最小路径和(Leecode 64 中等)
1.问题描述
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步
2.问题分析
其实动态问题只要考虑如何定义数据结构、结构的含义、状态转移方程的建立。
2.1 定义数据结构
问题是有多少不同的路径,此时应当使用dp[m-1][n-1]来表达最终的结果
2.2 结构含义的解读
本问题中dp[i][j]就可以解读为:i代表地图的行,j代表列
2.3 状态转移方程的建立
本问题中:
由于题目限定了我们只能往下或者往右 移动,因此我们按照「当前可选方向」进行分析:
当前位置只能 「往下」 移动,即有 dp[i][j] = dp[i-1][j]
当前位置只能 「往右」 移动,即有 dp[i][j] = dp[i][j-1]
当前位置即能 「往下」 也能 「往右」 移动,即有 dp[i][j] =dp[i][j-1] + dp[i-1][j]
推导过程:
dp[i][j]代表的是到达地图grid[i][j]点到达路径的经过的数字之和,那么往上递推一步:如何到达grid[i][j]点,只有两种方法:由前面的点往下或者往右进入到这个点,会得到(dp[i][j-1]的数字之和+grid[i][j])、(dp[i-1][j]的的数字之和+grid[i][j])两种方式,问题的结果是找到数字最小的,因此只要在这两种方式找最小的哪一个就可以了,因为dp[i][j-1]、dp[i-1][j]这两种方式已经是之前的最小值了,因此算出的dp[i][j]就是最小的。由此可推导出dp[i][j]的状态转移方程:dp[i][j]=min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j])
3.代码展示:
代码如下(示例):
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int n=grid[0].size();
int m=grid.size();
vector<vector<int>> dp(m, vector<int>(n));
dp[0][0]=grid[0][0];
for(int i=0;i<m;i++)
{
for(int j=0;j<n;j++)
{
if(i>0&&j>0)
{
dp[i][j]=min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]);
}
else if(i>0)
{
dp[i][j]=dp[i-1][j]+grid[i][j];
}
else if(j>0){
dp[i][j]=dp[i][j-1]+grid[i][j];
}
}
}
return dp[m-1][n-1];
}
};
总结
其实动态问题只要考虑如何定义数据结构、结构的含义、状态转移方程的建立。
数据结构大部分都是dp[i][j],难得是如何去定义dp[i][j]的含义、i代表的含义、j代表的含义
状态转移方程:其实就是考虑变化的东西:dp[i][j]和dp[i-1][j]、dp[i][j-1]的关系,这个需要根据问题来分析,通过问题的结果去分析dp[i][j]的上一步如何到达dp[i][j],比如dp[i][j]–>到达grid[i][j]的最小数字总和,dp[i-1][j]–>到达grid[i-1][j]的最小数字总和,dp[i-1][j]–>到达grid[i][j-1]的最小数字总和,这是一种递推思想,不能总是想最开始如何一步一步找到最小的,而是只需要找到从上一个最小的如何到达下一个最小的,这才是递推的思想。
边栏推荐
- The maximum number of words in the sentence of leetcode simple question
- LeetCode#118. Yanghui triangle
- 学习记录:使用STM32F1看门狗
- How to change XML attribute - how to change XML attribute
- ucore lab7
- How to build a nail robot that can automatically reply
- What if software testing is too busy to study?
- Market trend report, technical innovation and market forecast of Chinese hospital respiratory humidification equipment
- How to do agile testing in automated testing?
- Currently, mysql5.6 is used. Which version would you like to upgrade to?
猜你喜欢
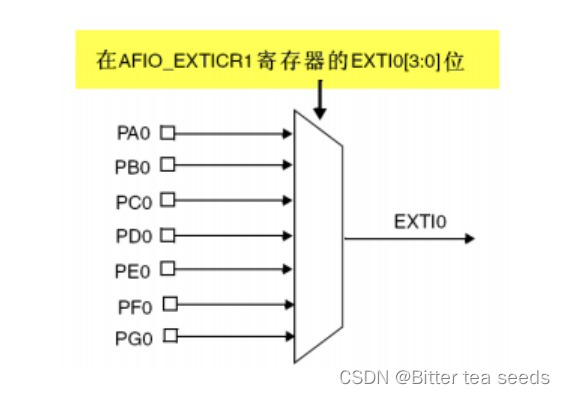
学习记录:使用STM32外部输入中断

線程及線程池
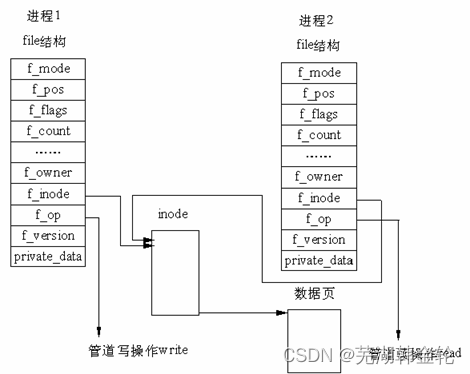
Lab 8 file system
What are the software testing methods? Show you something different
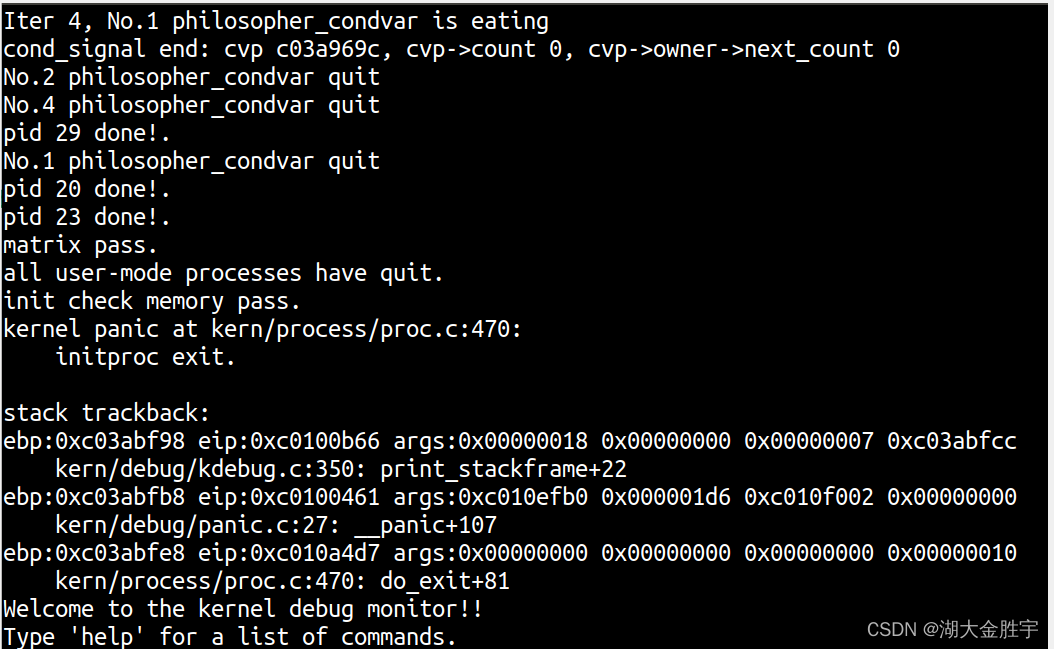
ucore lab7

Lab 8 文件系统

Servlet
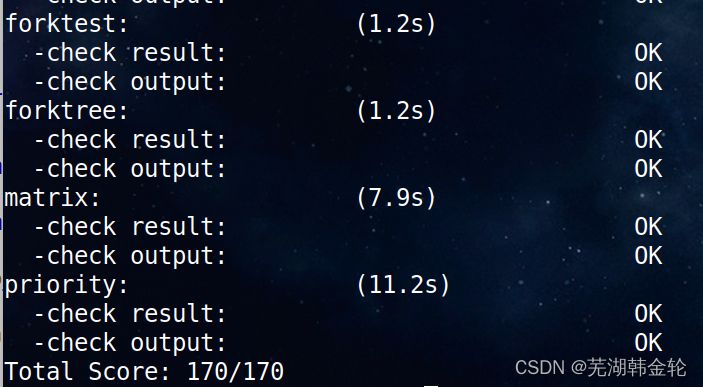
UCORE LaB6 scheduler experiment report
![[200 opencv routines] 98 Statistical sorting filter](/img/ba/9097df20f6d43dfce9fc1e374e6597.jpg)
[200 opencv routines] 98 Statistical sorting filter
Eslint--- error: newline required at end of file but not found (EOL last) solution
随机推荐
[200 opencv routines] 98 Statistical sorting filter
Do you know the performance testing terms to be asked in the software testing interview?
遇到程序员不修改bug时怎么办?我教你
UCORE lab8 file system experiment report
Portapack application development tutorial (XVII) nRF24L01 launch B
How to become a good software tester? A secret that most people don't know
ucore Lab 1 系统软件启动过程
接口测试面试题及参考答案,轻松拿捏面试官
软件测试面试要问的性能测试术语你知道吗?
Mysql database (II) DML data operation statements and basic DQL statements
How to do agile testing in automated testing?
软件测试工作太忙没时间学习怎么办?
The most detailed postman interface test tutorial in the whole network. An article meets your needs
ArrayList集合
The wechat red envelope cover designed by the object is free! 16888
Example 071 simulates a vending machine, designs a program of the vending machine, runs the program, prompts the user, enters the options to be selected, and prompts the selected content after the use
学习记录:使用STM32外部输入中断
Video scrolling subtitle addition, easy to make with this technique
Mysql database (III) advanced data query statement
FSM和i2c实验报告
