当前位置:网站首页>Matlab SEIR infectious disease model prediction
Matlab SEIR infectious disease model prediction
2022-07-07 23:21:00 【Goose feather is on the way】
List of articles
1. SEIR Model
Applicable to those who are susceptible 、 Exposed person 、 The sick and the convalescent 4 Quasi population , Have incubation period 、 Diseases that get lifelong immunity after cure , Such as herpes zoster 、 Chicken pox .
The model assumes
Suppose that the susceptible person becomes the exposed person after effective contact with the sick person , The exposed person becomes ill after the average incubation period , The sick can be cured and become a convalescent , The convalescent is no longer susceptible to lifelong immunity ; Take one day as the minimum time unit of the model .
The total number is N, Regardless of the birth and death of the population , Move in and out , This total number remains unchanged .
2. Demo1
N=330000000; % Population
load America.mat
% The first column is the cumulative number of confirmed cases , The second column is the cumulative number of deaths , The third column is the cumulative number of cured
E=0;% Lurker
D=0;% Number of dead patients
I=1;% Number of people infected
S=N-I;% Number of susceptible people
R=0;% Number of convalescents
r=17;% Number of infected people exposed
% r=19;
B=0.602;% The probability of infection
% a=0.17;% Probability of latent person turning into infected person
% a=0.175;
a=0.18;% Probability of latent person turning into infected person
% r2=8;% Number of contacts of lurks
r2=15;% Number of contacts of lurks
% B2=0.03;% The probability of a latent person infecting a normal person
B2=0.05;
y=0.000316893;% Rehabilitation probability
k=0.01;% Daily mortality
B3=0.001;% Negative conversion rate
% T=1:200;
T=1:180;
for idx=1:length(T)-1
% The time for the government to issue the call for control and the response delay in various places , Here the 11 Days later is the critical point ,
% amount to 11 Days later , The mobility and medical allocation of infected and latent people have changed significantly , Specifically, the number of contacts
if idx>=14
r=0.20;% Number of infected people exposed
r2=1.8;% The number of infected people contacting
y=0.15;% The recovery rate rises
a=0.12;% Probability of latent person turning into infected person
k=0.0001;% The daily mortality rate remains unchanged
end
if idx<11
S(idx+1)=S(idx)-r*B*S(idx)*I(idx)/N-r2*B2*S(idx)*E(idx)/N;% Iteration of susceptible people
E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)+r2*B2*S(idx)*E(idx)/N;% Lurker iteration
I(idx+1)=I(idx)+a*E(idx)-(k+y)*I(idx);% The number of infected people iterates
R(idx+1)=R(idx)+0.05*I(idx);% Number of rehabilitated patients
D(idx+1)=R(idx)+k*I(idx);% Number of dead patients
else
S(idx+1)=S(idx)-r*B*S(idx)*I(idx)/N-r2*B2*S(idx)*E(idx)/N+B3*E(idx-10);% Iteration of susceptible people
E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)+r2*B2*S(idx)*E(idx)/N-B3*E(idx-10);% Lurker iteration
I(idx+1)=I(idx)+a*E(idx)-(k+y)*I(idx);% The number of infected people iterates
% Y There is a problem with the parameters
R(idx+1)=R(idx)+0.045*I(idx-9);% Number of rehabilitated patients
D(idx+1)=R(idx)+k*I(idx);% Number of dead patients
end
end
B={
'01-19','02-08','02-28','03-19','04-08','04-28','05-18','06-07','06-27','07-17','08-06'};
% plot(1:1:102,huibei(:,1)-huibei(:,2)-huibei(:,3),'r*');hold on
plot(1:1:133,America(:,1)-America(:,2)-America(:,3),'g-');hold on
plot(1:1:133,America(:,3),'k-');hold on
% legend(' Actual illness ',' Actual rehabilitation ')
% xlabel(' Days ');
% ylabel(' The number of ');
% legend(' Actual illness ')
plot(T,R,'b',T,I,'r');
grid on;
hold on;
plot([7 7],[0 1000]);
set(gca,'XTickLabel',B)
xlabel(' date ');
ylabel(' The number of ');
legend(' Actual illness ',' Actual rehabilitation ',' Predict the rehabilitation ',' Predict patients ');
title(' Taking isolation measures SEIR Model ');
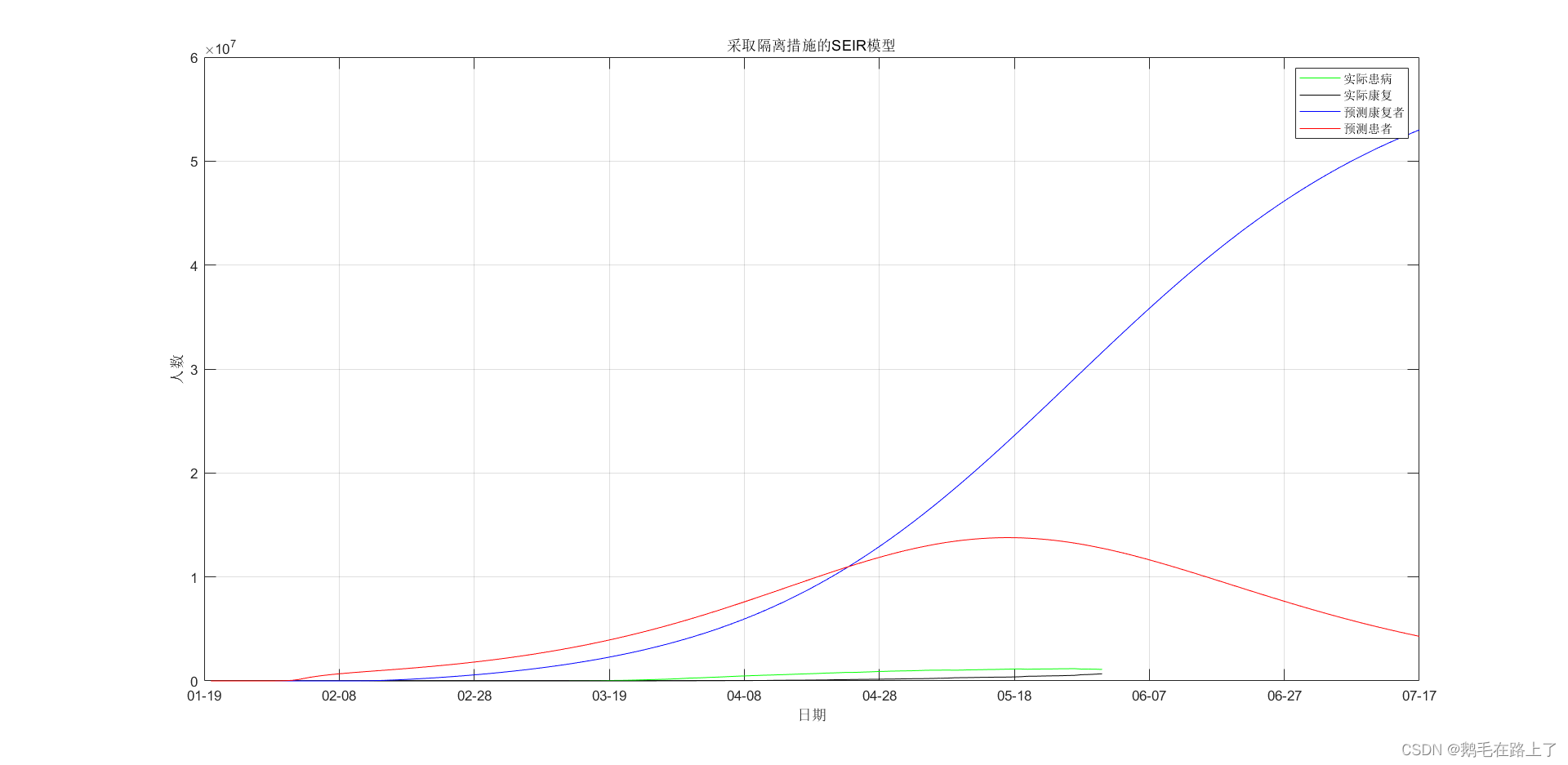
3. Demo2
% hypothesis 1 month 15 The first confirmed case began to appear on the th ,1 month 23 The city was closed on the th , At this time, other provinces and cities also respond to isolation measures , About distance 15 After 11 Government control plays an obvious role
N=1395380000; % Population
load quanguo1.mat
% The first column is the cumulative number of confirmed cases , The second column is the cumulative number of deaths , The third column is the cumulative number of cured
E=0;% Lurker
D=0;% Number of dead patients
I=1;% Number of people infected
S=N-I;% Number of susceptible people
R=0;% Number of convalescents
r=17;% Number of infected people exposed
% r=19;
B=0.602;% The probability of infection
% a=0.17;% Probability of latent person turning into infected person
% a=0.175;
a=0.298;% Probability of latent person turning into infected person
% r2=8; % Number of contacts of lurks
r2=15;% Number of contacts of lurks
% B2=0.03;% The probability of a latent person infecting a normal person
B2=0.05;
y=0.05;% Rehabilitation probability
k=0.0001;% Daily mortality
B3=0.1;% Negative conversion rate
% T=1:200;
T=1:180;
for idx=1:length(T)-1
% If the 1 month 18 Japan is the starting point of the epidemic , The time for the government to issue the call for control and the response delay in various places , Here the 11 Days later is the critical point ,
% amount to 11 Days later , The mobility and medical allocation of infected and latent people have changed significantly , Specifically, the number of contacts
if idx>=11
r=0.20;% Number of infected people exposed
r2=1.8;% The number of infected people contacting
y=0.15;% The recovery rate rises
a=0.12;% Probability of latent person turning into infected person
k=0.0001;% The daily mortality rate remains unchanged
end
if idx<11
S(idx+1)=S(idx)-r*B*S(idx)*I(idx)/N-r2*B2*S(idx)*E(idx)/N;% Iteration of susceptible people
E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)+r2*B2*S(idx)*E(idx)/N;% Lurker iteration
I(idx+1)=I(idx)+a*E(idx)-(k+y)*I(idx);% The number of infected people iterates
R(idx+1)=R(idx)+0.05*I(idx);% Number of rehabilitated patients
D(idx+1)=R(idx)+k*I(idx);% Number of dead patients
else
S(idx+1)=S(idx)-r*B*S(idx)*I(idx)/N-r2*B2*S(idx)*E(idx)/N+B3*E(idx-10);% Iteration of susceptible people
E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)+r2*B2*S(idx)*E(idx)/N-B3*E(idx-10);% Lurker iteration
I(idx+1)=I(idx)+a*E(idx)-(k+y)*I(idx);% The number of infected people iterates
% Y There is a problem with the parameters
R(idx+1)=R(idx)+0.045*I(idx-9);% Number of rehabilitated patients
D(idx+1)=R(idx)+k*I(idx);% Number of dead patients
end
end
B={
'01-19','02-08','02-28','03-19','04-08','04-28','05-18','06-07','06-27','07-17','08-06'};
% plot(1:1:102,huibei(:,1)-huibei(:,2)-huibei(:,3),'r*');hold on
plot(1:1:137,quanguo1(:,1)-quanguo1(:,2)-quanguo1(:,3),'g-');hold on
plot(1:1:137,quanguo1(:,3),'k-');hold on
% legend(' Actual illness ',' Actual rehabilitation ')
% xlabel(' Days ');
% ylabel(' The number of ');
% legend(' Actual illness ')
plot(T,R,'b',T,I,'r');
grid on;
hold on;
plot([7 7],[0 1000]);
set(gca,'XTickLabel',B)
xlabel(' date ');
ylabel(' The number of ');
legend(' Actual illness ',' Actual rehabilitation ',' Predict the rehabilitation ',' Predict patients ');
title(' Taking isolation measures SEIR Model ');
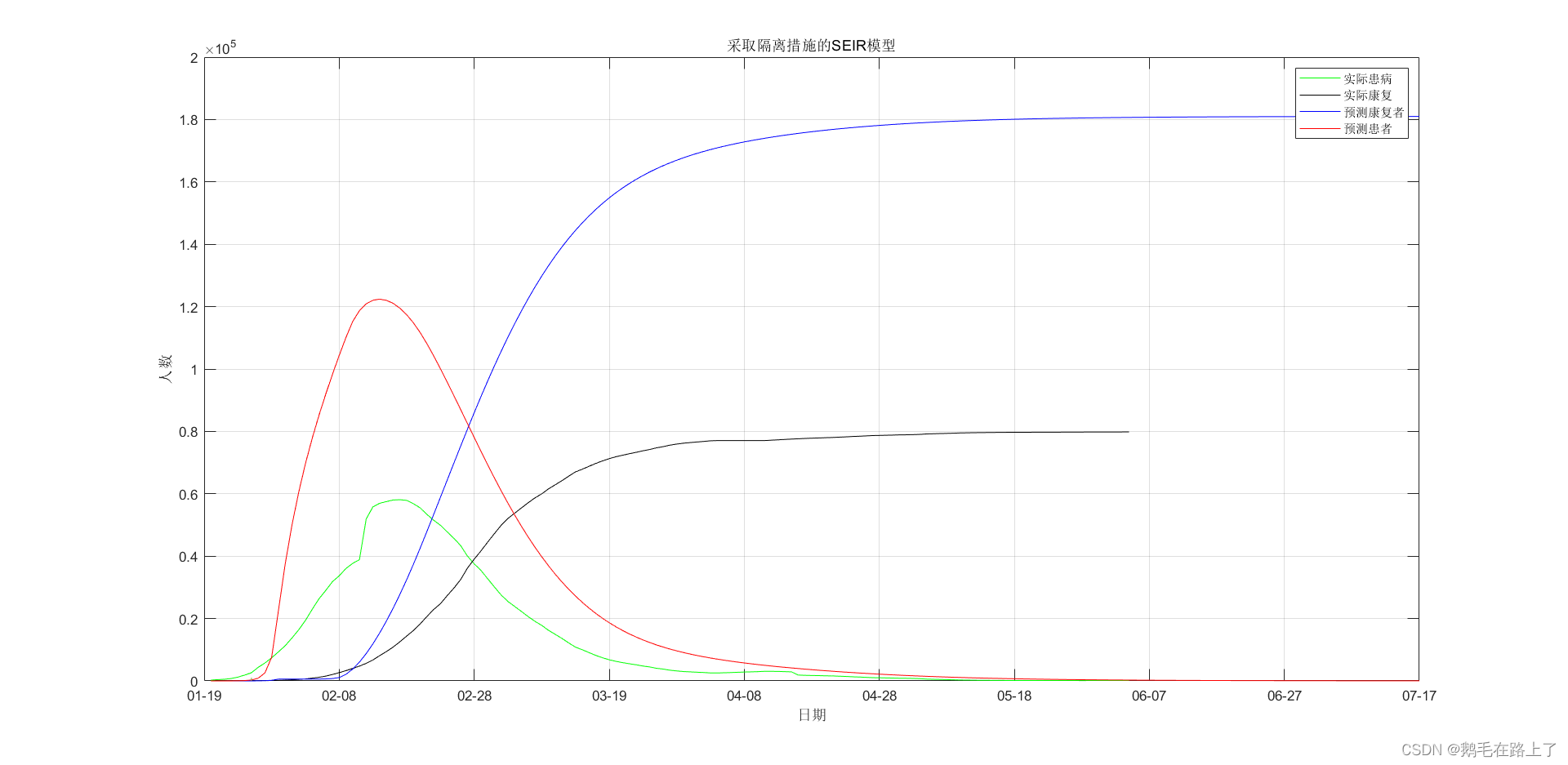
4. data
1. America.mat
1.0 0.0 0.0
1.0 0.0 0.0
2.0 0.0 0.0
2.0 0.0 0.0
3.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
12.0 0.0 1.0
12.0 0.0 1.0
12.0 0.0 3.0
12.0 0.0 3.0
12.0 0.0 3.0
13.0 0.0 3.0
13.0 0.0 3.0
14.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
34.0 0.0 3.0
34.0 0.0 3.0
34.0 0.0 3.0
53.0 0.0 3.0
57.0 0.0 3.0
60.0 0.0 3.0
60.0 0.0 3.0
64.0 0.0 3.0
69.0 1.0 3.0
89.0 2.0 3.0
106.0 6.0 3.0
126.0 9.0 3.0
161.0 11.0 3.0
233.0 14.0 3.0
338.0 17.0 10.0
445.0 19.0 10.0
572.0 22.0 10.0
717.0 26.0 10.0
1004.0 31.0 10.0
1323.0 38.0 10.0
1832.0 41.0 31.0
2291.0 50.0 41.0
2995.0 60.0 56.0
3782.0 69.0 56.0
5073.0 90.0 56.0
6536.0 116.0 106.0
10525.0 153.0 108.0
14387.0 204.0 121.0
19624.0 260.0 147.0
27111.0 346.0 178.0
39183.0 473.0 178.0
46450.0 586.0 178.0
55231.0 797.0 354.0
69197.0 1046.0 619.0
86012.0 1301.0 753.0
104860.0 1711.0 894.0
124868.0 2190.0 2612.0
143724.0 2566.0 4865.0
165764.0 3170.0 5945.0
189753.0 4081.0 7141.0
216722.0 5137.0 8672.0
255456.0 6532.0 9359.0
288993.0 7793.0 9897.0
312249.0 8503.0 15021.0
337300.0 9627.0 17582.0
374782.0 11697.0 19972.0
400549.0 12907.0 22461.0
431694.0 14789.0 24213.0
469464.0 16711.0 26522.0
503177.0 18777.0 29191.0
529112.0 20549.0 30548.0
556569.0 22063.0 32634.0
587815.0 23599.0 37315.0
614726.0 26126.0 38879.0
650833.0 32707.0 52739.0
679766.0 34705.0 57844.0
709036.0 37104.0 63510.0
740151.0 39193.0 68456.0
765738.0 40670.0 71281.0
792846.0 42491.0 72410.0
825041.0 45340.0 82973.0
849094.0 47684.0 84050.0
886709.0 50243.0 85922.0
929028.0 52371.0 110504.0
960896.0 54265.0 118162.0
987916.0 55425.0 118781.0
1012147.0 56933.0 139419.0
1036417.0 59284.0 143098.0
1065739.0 61715.0 147473.0
1099275.0 63972.0 156089.0
1134059.0 65886.0 161782.0
1163372.0 67535.0 173910.0
1191849.0 68702.0 178671.0
1214023.0 69974.0 188069.0
1239847.0 72381.0 201152.0
1265212.0 74881.0 213126.0
1293907.0 76998.0 217251.0
1324352.0 78701.0 223930.0
1349599.0 80101.0 238081.0
1369943.0 80846.0 256345.0
1388283.0 82018.0 262326.0
1411148.0 83564.0 298643.0
1433375.0 85334.0 310415.0
1460902.0 87025.0 318036.0
1487065.0 88603.0 327774.0
1509444.0 90142.0 339572.0
1531737.0 91061.0 346786.0
1552304.0 92072.0 358918.0
1571328.0 93561.0 361227.0
1595318.0 95021.0 370973.0
1622337.0 96385.0 382936.0
1648283.0 97732.0 403312.0
1668493.0 98706.0 446982.0
1689581.0 99381.0 451745.0
1709388.0 99909.0 465668.0
1728954.0 100686.0 480273.0
1749160.0 102241.0 490256.0
1771631.0 103417.0 499113.0
1796810.0 104626.0 519715.0
1819788.0 105634.0 535371.0
1839679.0 106261.0 599882.0
1861474.0 106990.0 615654.0
1882478.0 108104.0 646414.0
1902031.0 109146.0 688670.0
2. quanguo1.mat
291.0 6.0 25.0
440.0 9.0 25.0
571.0 17.0 25.0
830.0 25.0 34.0
1287.0 41.0 38.0
1975.0 56.0 49.0
2744.0 80.0 51.0
4515.0 106.0 60.0
5974.0 132.0 103.0
7711.0 170.0 124.0
9692.0 213.0 171.0
11791.0 259.0 243.0
14380.0 304.0 328.0
17205.0 361.0 475.0
20438.0 425.0 632.0
24324.0 490.0 892.0
28018.0 563.0 1153.0
31161.0 636.0 1540.0
34594.0 723.0 2052.0
37162.0 812.0 2651.0
40224.0 909.0 3283.0
42708.0 1017.0 3998.0
44730.0 1114.0 4742.0
58839.0 1260.0 5646.0
63932.0 1381.0 6728.0
66575.0 1524.0 8101.0
68584.0 1666.0 9425.0
70637.0 1772.0 10860.0
72528.0 1870.0 12561.0
74276.0 2006.0 14387.0
75101.0 2121.0 16168.0
75993.0 2239.0 18277.0
76392.0 2348.0 20672.0
76846.0 2445.0 22907.0
77262.0 2595.0 24757.0
77779.0 2666.0 27353.0
78190.0 2718.0 29775.0
78630.0 2747.0 32531.0
78959.0 2791.0 36157.0
79389.0 2838.0 39049.0
79968.0 2873.0 41675.0
80174.0 2915.0 44518.0
80302.0 2946.0 47260.0
80422.0 2984.0 49914.0
80565.0 3015.0 52109.0
80710.0 3045.0 53793.0
80813.0 3073.0 55477.0
80859.0 3100.0 57143.0
80904.0 3123.0 58684.0
80924.0 3140.0 59982.0
80955.0 3162.0 61567.0
80992.0 3173.0 62887.0
81003.0 3180.0 64216.0
81021.0 3194.0 65649.0
81048.0 3204.0 67022.0
81077.0 3218.0 67863.0
81116.0 3231.0 68799.0
81151.0 3242.0 69725.0
81235.0 3250.0 70547.0
81300.0 3253.0 71284.0
81416.0 3261.0 71876.0
81498.0 3267.0 72382.0
81600.0 3276.0 72841.0
81747.0 3283.0 73299.0
81846.0 3287.0 73791.0
81960.0 3293.0 74196.0
82078.0 3298.0 74737.0
82213.0 3301.0 75122.0
82341.0 3306.0 75600.0
82447.0 3311.0 75937.0
82545.0 3314.0 76225.0
82631.0 3321.0 76415.0
82724.0 3327.0 76610.0
82802.0 3331.0 76785.0
82875.0 3335.0 76984.0
82930.0 3338.0 77055.0
83005.0 3340.0 77055.0
83071.0 3340.0 77055.0
83157.0 3342.0 77055.0
83249.0 3344.0 77055.0
83305.0 3345.0 77055.0
83369.0 3349.0 77055.0
83482.0 3349.0 77055.0
83597.0 3351.0 77180.0
83696.0 3351.0 77297.0
83745.0 3352.0 77424.0
83797.0 3352.0 77539.0
84149.0 4642.0 77635.0
84180.0 4642.0 77744.0
84201.0 4642.0 77825.0
84237.0 4642.0 77895.0
84250.0 4642.0 77978.0
84287.0 4642.0 78042.0
84302.0 4642.0 78147.0
84311.0 4642.0 78236.0
84324.0 4642.0 78362.0
84338.0 4643.0 78450.0
84341.0 4643.0 78558.0
84347.0 4643.0 78664.0
84367.0 4643.0 78712.0
84369.0 4643.0 78766.0
84373.0 4643.0 78816.0
84387.0 4643.0 78893.0
84391.0 4643.0 78911.0
84393.0 4643.0 78966.0
84403.0 4643.0 79043.0
84404.0 4643.0 79182.0
84407.0 4643.0 79246.0
84414.0 4643.0 79305.0
84416.0 4643.0 79361.0
84416.0 4643.0 79418.0
84435.0 4643.0 79510.0
84450.0 4644.0 79538.0
84451.0 4644.0 79585.0
84461.0 4644.0 79616.0
84465.0 4644.0 79635.0
84471.0 4644.0 79660.0
84478.0 4644.0 79679.0
84487.0 4645.0 79700.0
84494.0 4645.0 79705.0
84503.0 4645.0 79715.0
84506.0 4645.0 79720.0
84516.0 4645.0 79736.0
84522.0 4645.0 79738.0
84522.0 4645.0 79743.0
84525.0 4645.0 79751.0
84536.0 4645.0 79762.0
84543.0 4645.0 79772.0
84545.0 4645.0 79780.0
84547.0 4645.0 79791.0
84561.0 4645.0 79800.0
84569.0 4645.0 79806.0
84572.0 4645.0 79809.0
84593.0 4645.0 79822.0
84603.0 4645.0 79826.0
84602.0 4645.0 79827.0
84608.0 4645.0 79834.0
Refer to the post :
K2I-matlab Establish a model to predict infectious diseases
边栏推荐
猜你喜欢

Wechat forum exchange applet system graduation design completion (7) Interim inspection report
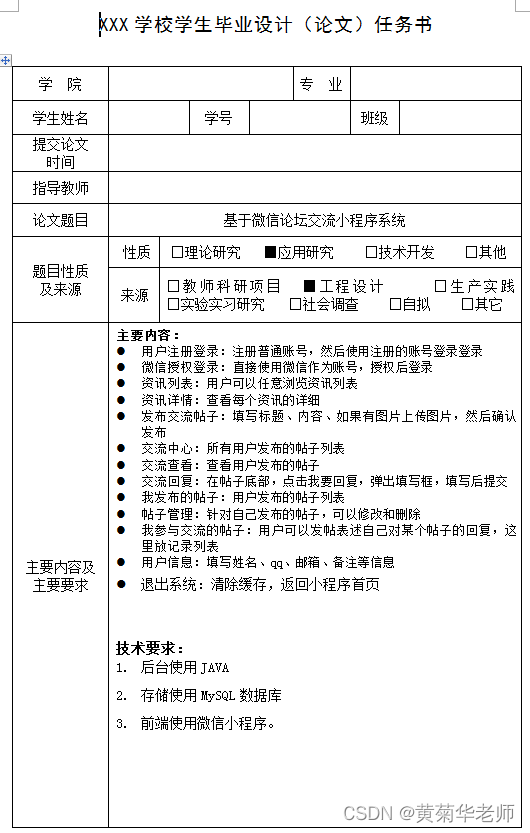
微信论坛交流小程序系统毕业设计毕设(5)任务书
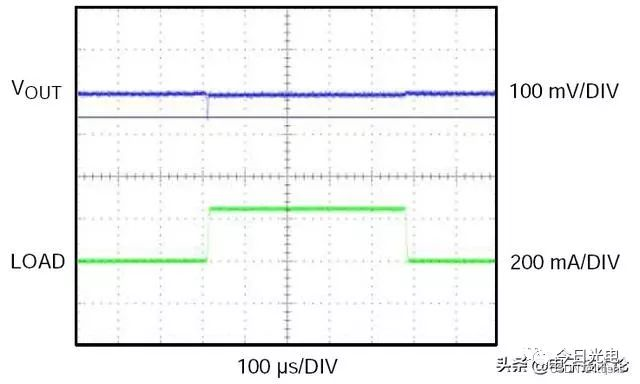
Puce à tension stabilisée LDO - schéma de bloc interne et paramètres de sélection du modèle

JS get the key and value of the object

海内外技术人们“看”音视频技术的未来
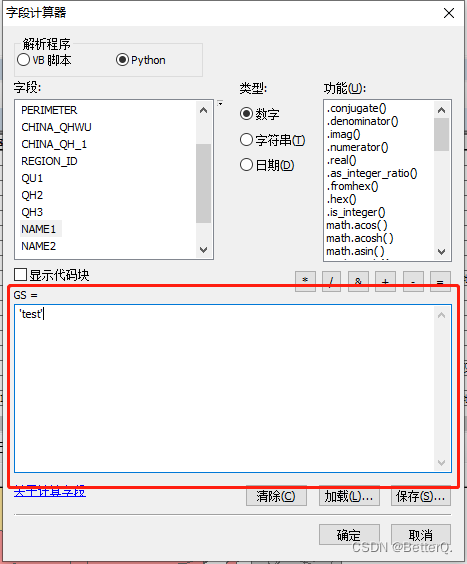
ArcGIS:字段赋值_属性表字段计算器(Field Calculator)依据条件为字段赋值

re1攻防世界逆向
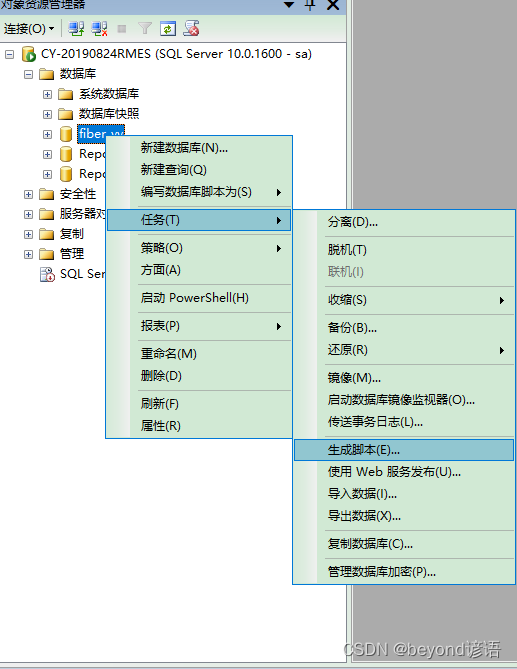
十四、数据库的导出和导入的两种方法
UE4_UE5全景相机

Unity3D学习笔记6——GPU实例化(1)
随机推荐
十三、系统优化
Inftnews | the wide application of NFT technology and its existing problems
USB(十六)2022-04-28
ArcGIS: field assignment_ The attribute table field calculator assigns values to fields based on conditions
php 使用阿里云存储
深入理解Mysql锁与事务隔离级别
How to generate unique file names
Freelink open source call center design idea
LeeCode -- 6. Z 字形变换
Dynamics 365 find field filtering
微信论坛交流小程序系统毕业设计毕设(3)后台功能
JMeter-接口自动化测试读取用例,执行并结果回写
Technology at home and abroad people "see" the future of audio and video technology
网络安全-永恒之蓝
Network security - Eternal Blue
系统架构设计师备考经验分享:论文出题方向
Dynamic agent explanation (July 16, 2020)
Redhat下安装fedora
What are the similarities and differences between smart communities and smart cities
在软件工程领域,搞科研的这十年!