当前位置:网站首页>cf:C. The Third Problem【关于排列这件事】
cf:C. The Third Problem【关于排列这件事】
2022-07-06 00:38:00 【白速龙王的回眸】

分析
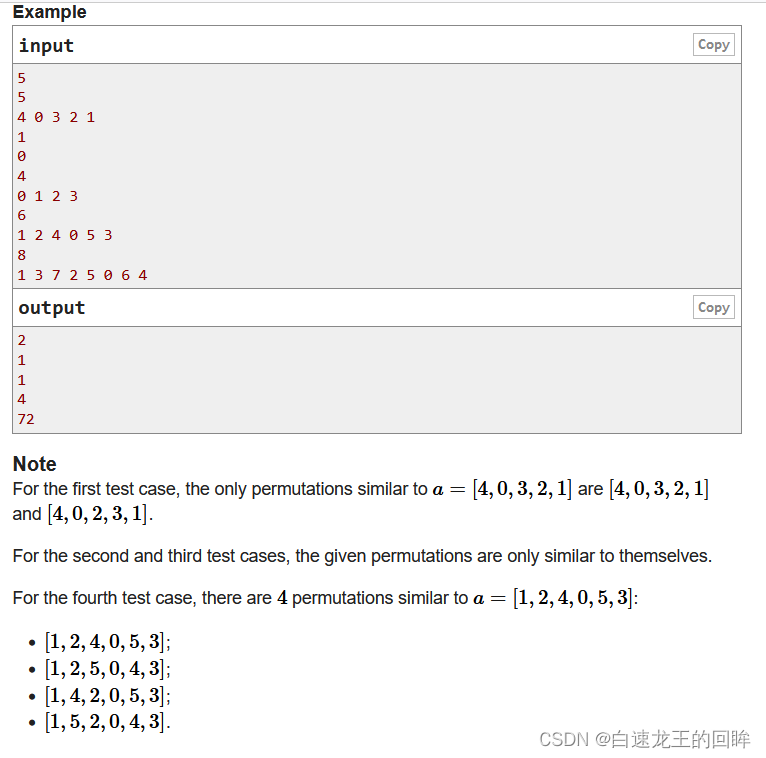
这是一道排列的题
看起来花里胡哨的
说到排列,我们就要找到这个排列0到n对应的下标位置
我们这里的MET定义是除字串外最小的数,所有的字串都要满足这个最小的数相同
于是,我们遵循“最小”,从最小的0开始一个个找对应的索引
首先0的位置肯定变不了,其次1也变不了(否则总能找到一个区间使得MET不等)
然后看2后面的数,用lr维护当前索引区间的左右,然后如果2在lr中的话,它就有r - l + 1 - 2种选择
如果它在索引区间lr外,那么必定有一种区间的选择使得MET不等,为了更形象,举个例子:
+++2+++1+++0+(1)
++2++++1+++0+(2)
----+++++++++++
如果我们选上一行+的区间,那显然MET(1) > 2而 MET(2) = 2
因此当我们选第k个数的时候,上一个lr索引区间长度是r - l + 1
我们只有当id[i]在索引区间内才可以相似,这时候它能选的位置个数共有r - l + 1 - i
用ans 连乘就可以了
ac code
import sys
input = sys.stdin.readline
MOD = 10 ** 9 + 7
for _ in range(int(input())):
n = int(input())
a = list(map(int, input().split()))
id = [0] * n
for i, v in enumerate(a):
id[v] = i
# we judge from v = 0,1,...
ans = 1
l = r = id[0]
for i in range(1, n):
# if id[i] outside [l, r], no other choice
# cause there must be a choice MET not equal
if id[i] < l or id[i] > r:
l, r = min(id[i], l), max(id[i], r)
else:
ans = ans * (r - l + 1 - i) % MOD
print(ans)
总结
排列 + 排序 + 区间内外模拟
通过排除一些情况从而猜测合理的情况
边栏推荐
- 数据分析思维分析方法和业务知识——分析方法(二)
- 2022-02-13 work record -- PHP parsing rich text
- MIT博士论文 | 使用神经符号学习的鲁棒可靠智能系统
- Anconda download + add Tsinghua +tensorflow installation +no module named 'tensorflow' +kernelrestart: restart failed, kernel restart failed
- Browser local storage
- curlpost-php
- Global and Chinese markets for hinged watertight doors 2022-2028: Research Report on technology, participants, trends, market size and share
- Spark-SQL UDF函数
- [groovy] compile time metaprogramming (compile time method interception | find the method to be intercepted in the myasttransformation visit method)
- [Chongqing Guangdong education] reference materials for Zhengzhou Vocational College of finance, taxation and finance to play around the E-era
猜你喜欢
免费的聊天机器人API
时间戳的拓展及应用实例

Anconda download + add Tsinghua +tensorflow installation +no module named 'tensorflow' +kernelrestart: restart failed, kernel restart failed

Introduction of motor

Browser local storage
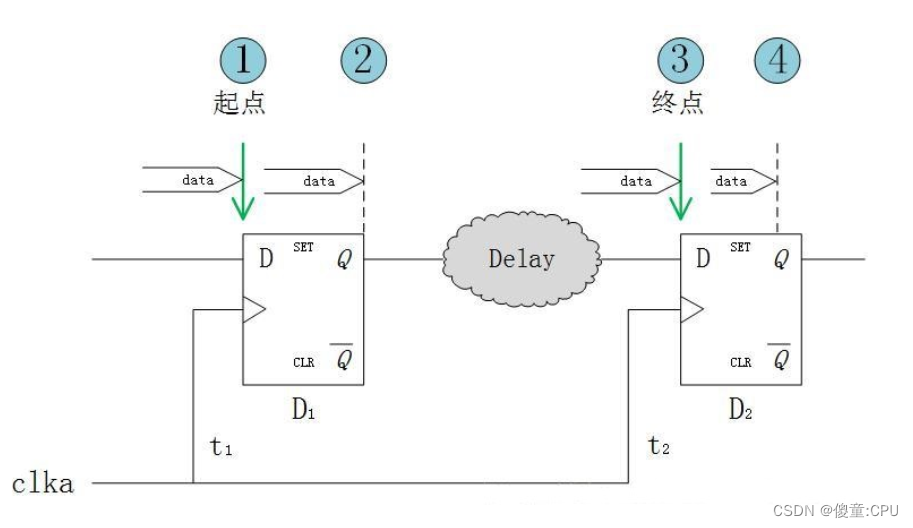
Model analysis of establishment time and holding time
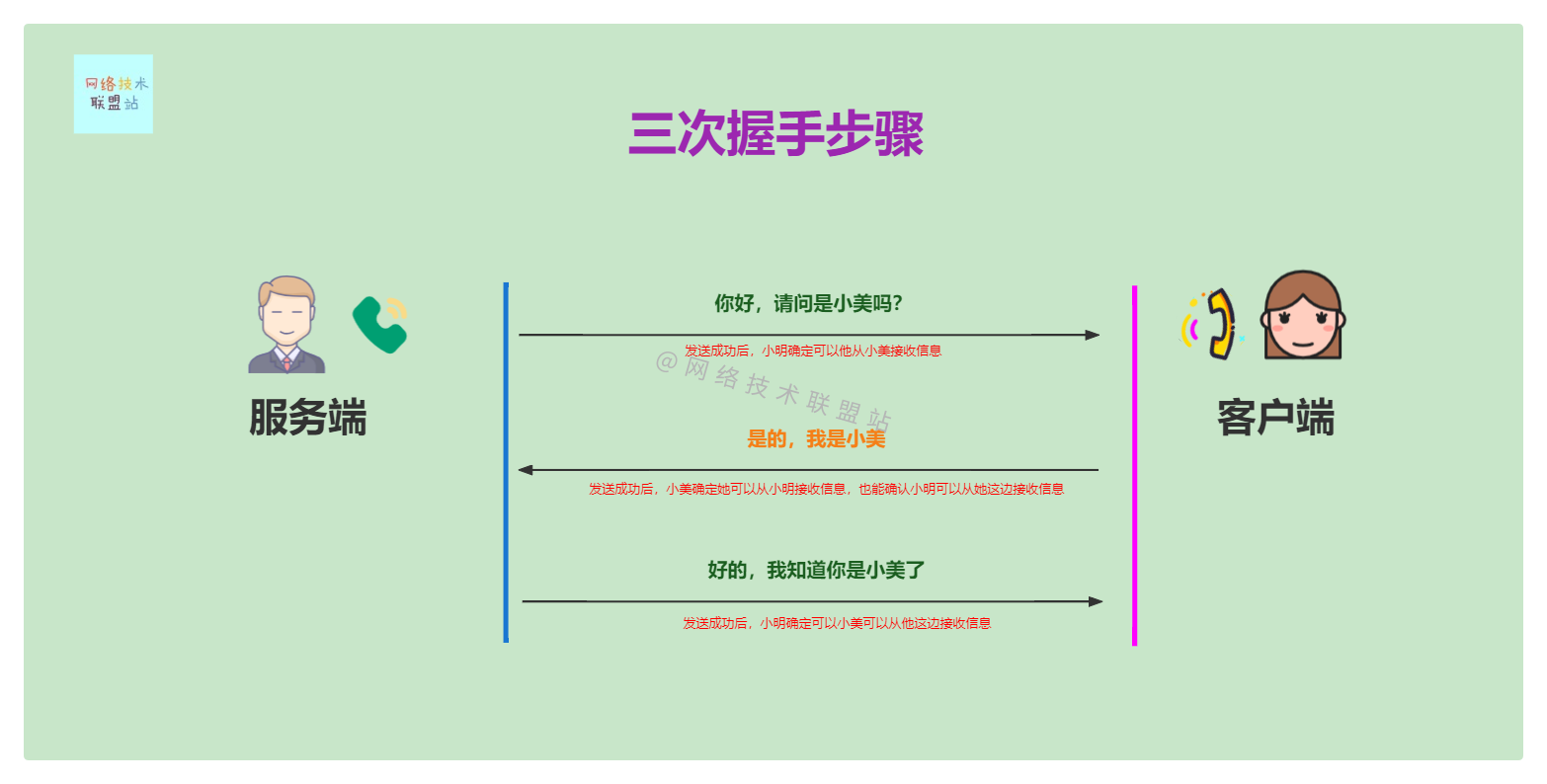
图解网络:TCP三次握手背后的原理,为啥两次握手不可以?

电机的简介
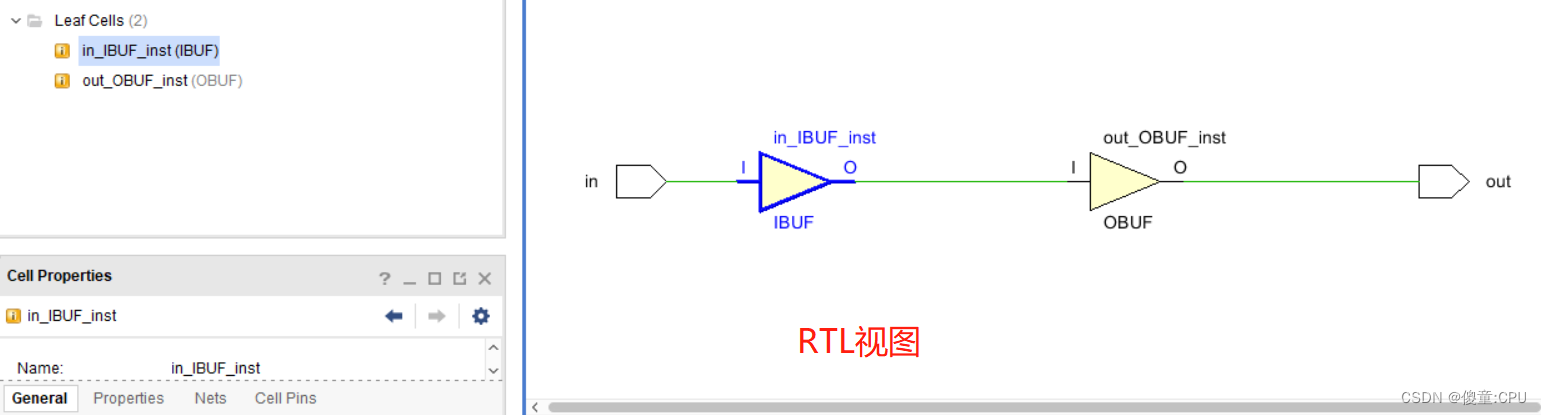
The relationship between FPGA internal hardware structure and code

State mode design procedure: Heroes in the game can rest, defend, attack normally and attack skills according to different physical strength values.
随机推荐
【线上小工具】开发过程中会用到的线上小工具合集
devkit入门
Curlpost PHP
Idea remotely submits spark tasks to the yarn cluster
Search (DFS and BFS)
Basic introduction and source code analysis of webrtc threads
Leetcode 450 deleting nodes in a binary search tree
LeetCode 8. String conversion integer (ATOI)
[designmode] Decorator Pattern
Browser local storage
Codeforces round 804 (Div. 2) [competition record]
Go learning --- read INI file
Classical concurrency problem: the dining problem of philosophers
Pointer pointer array, array pointer
Location based mobile terminal network video exploration app system documents + foreign language translation and original text + guidance records (8 weeks) + PPT + review + project source code
新手入门深度学习 | 3-6:优化器optimizers
Analysis of the combination of small program technology advantages and industrial Internet
[groovy] compile time meta programming (AST syntax tree conversion with annotations | define annotations and use groovyasttransformationclass to indicate ast conversion interface | ast conversion inte
[Online gadgets] a collection of online gadgets that will be used in the development process
XML配置文件