当前位置:网站首页>Solutions of ordinary differential equations (2) examples
Solutions of ordinary differential equations (2) examples
2022-07-05 08:44:00 【Royal fox God double blazing】
use SciPyのscipy.integrate.odeint Solve simultaneous differential equations , In time t(tの The scope is 0~ Just a few seconds , example :t=0~2 second ) Reconciliation x(t), y(t), z(t) Make a picture .
As t=0 Initial conditions of ,x(t=0) = -10, y (t=0) = 0, z (t=0) = 35.0. also , About the coefficient a,b,c, You can try a = 40, b = 5, c = 35 And a = 40, b = 10, c = 35 The situation of . And time division Δt Take a smaller value appropriately . in addition ,Δt If it is too small , The amount of calculation will become very large . Adjust according to the errors after the actual implementation .
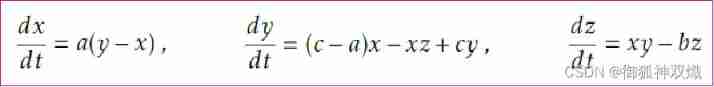
Here are the solutions python Program :
import numpy as np
import scipy.integrate as sciin
import matplotlib.pyplot as plt
# Compare with the independent variable t The function name of the related derivative function is placed in F in
def f(F, t,params):
x,y,z = F
f_values = [a*(y-x),(c-a)*x-x*z+c*y,x*y-b*z] # Write separately x,y,z The derivative of is equal to the formula on the right of
return f_values
# Amplification coefficient
a = 40
b= 5
c = 35
# Put the above three coefficients into parameters in
parameters = [a,b,c]
# Set up x,y,z The initial value of the
x0 = -10
y0 = 0.0
z0 = 35
# Put the initial value into Y0 in
Y0 = [x0,y0,z0]
# Starting point , The end point , Interval setting
tStart = 0.0
tStop = 2
tInc = 0.01 # interval
# Summarize the above to t in
t = np.arange(tStart, tStop, tInc)
# sciin.odeint Explain ODE
solution = sciin.odeint(f, Y0, t, args=(parameters,))
# Make a picture
plt.figure(figsize=(9.5, 6.5))
plt.plot(t, solution[:, 0], color='black')
plt.plot(t, solution[:, 1], color='green')
plt.plot(t, solution[:, 2], color='red')
plt.xlabel('time, t' , fontsize=14)
plt.ylabel('theta(t)', fontsize=14)
plt.show()
I'm a genius .
边栏推荐
猜你喜欢
Business modeling of software model | overview
Typescript hands-on tutorial, easy to understand

Halcon snap, get the area and position of coins

Guess riddles (2)
Meizu Bluetooth remote control temperature and humidity access homeassistant

【NOI模拟赛】汁树(树形DP)

猜谜语啦(7)
深度学习模型与湿实验的结合,有望用于代谢通量分析

Example 006: Fibonacci series
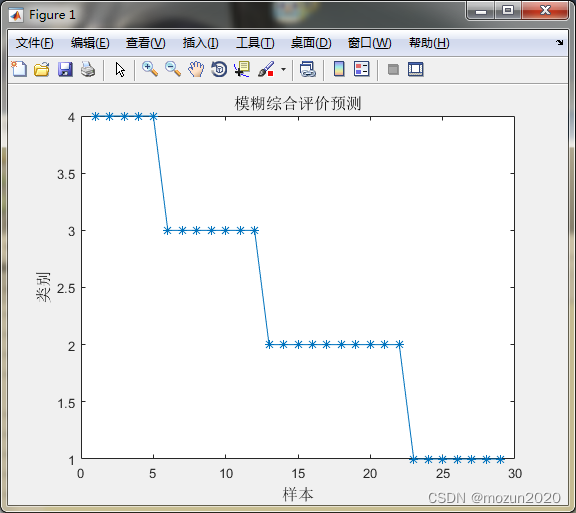
MATLAB skills (28) Fuzzy Comprehensive Evaluation
随机推荐
Typical low code apaas manufacturer cases
Guess riddles (6)
Halcon affine transformations to regions
Example 003: a complete square is an integer. It is a complete square after adding 100, and it is a complete square after adding 168. What is the number?
Reasons for the insecurity of C language standard function scanf
kubeadm系列-00-overview
287. Looking for repeats - fast and slow pointer
Esp8266 interrupt configuration
我从技术到产品经理的几点体会
[matlab] matlab reads and writes Excel
Adaboost使用
整形的分类:short in long longlong
轮子1:QCustomPlot初始化模板
Arrangement of some library files
C# LINQ源码分析之Count
319. 灯泡开关
Guess riddles (5)
Example 009: pause output for one second
Low code platform | apaas platform construction analysis
MATLAB小技巧(28)模糊綜合評價