当前位置:网站首页>二叉树递归套路总结
二叉树递归套路总结
2022-07-05 22:50:00 【明朗晨光】
之前所有用到二叉树递归套路的时间复杂度都是 O ( N ) O(N) O(N),其中 N N N 是二叉树的节点个数,且都是最优解。
某个节点从左右孩子获取信息,然后整合到该节点,此时的左右孩子已经不需要了,而该节点的父节点也是重复这个过程,整个过程相当于后序遍历,在树上做动态规划,所以叫做树型dp。
这个套路包括两个层次:
思想提醒
目标如何实现:X 为根节点的二叉树如何实现目标?
实现手段:向左右树要信息,列举可能性,这个可能性一定是基于从左右树要来的信息(常数时间内可以得到的),加工出来的同等量级的信息也是常数时间的。
设计信息体,分析可能性,常见的分类是 “与目标 X 有关” 和 “与目标 X 无关”。模板
① 设计Info信息体;
②process函数:process函数一定要返回Info;遇到空的时候,如果值不好设置就返回空,如果好设置就设置;
③默认先得到左树信息,然后得到右树信息;
④分析完可能性后,把 X 需要的信息都加工出来,这是高度模板化的。
这个套路可以解决绝大多数的二叉树问题尤其是树型dp问题,本质是利用 递归遍历二叉树 的便利性。
整个流程总结如下:
1)假设以 X 节点为根,假设可以向 X 左树和 X 右树要任何信息
2)在上一步的假设下,讨论以 X 为根节点的树,得到答案的可能性(最重要)
3)列出所有可能性后,确定到底需要向左树和右树要什么样的信息
4)把左树信息和右树信息求全集,就是任何一棵子树都需要返回的信息S
5)递归函数都返回S,每一棵子树都这么要求
6)写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息
边栏推荐
- openresty ngx_ Lua request response
- Realize reverse proxy client IP transparent transmission
- Commonly used probability distributions: Bernoulli distribution, binomial distribution, polynomial distribution, Gaussian distribution, exponential distribution, Laplace distribution and Dirac delta d
- 第一讲:蛇形矩阵
- The code generator has deoptimised the styling of xx/typescript. js as it exceeds the max of 500kb
- Week 17 homework
- 如何快速理解复杂业务,系统思考问题?
- 一文搞定JVM的内存结构
- Leetcode weekly The 280 game of the week is still difficult for the special game of the week's beauty team ~ simple simulation + hash parity count + sorting simulation traversal
- 3 find the greatest common divisor and the least common multiple
猜你喜欢
Using LNMP to build WordPress sites
Element positioning of Web Automation
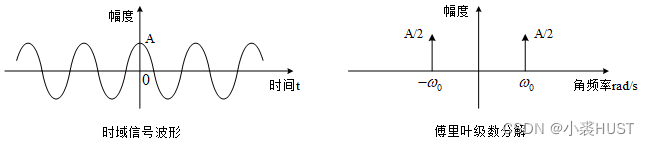
Overview of Fourier analysis
The method and principle of viewing the last modification time of the web page

Double pointer of linked list (fast and slow pointer, sequential pointer, head and tail pointer)
Editor extensions in unity
Common model making instructions
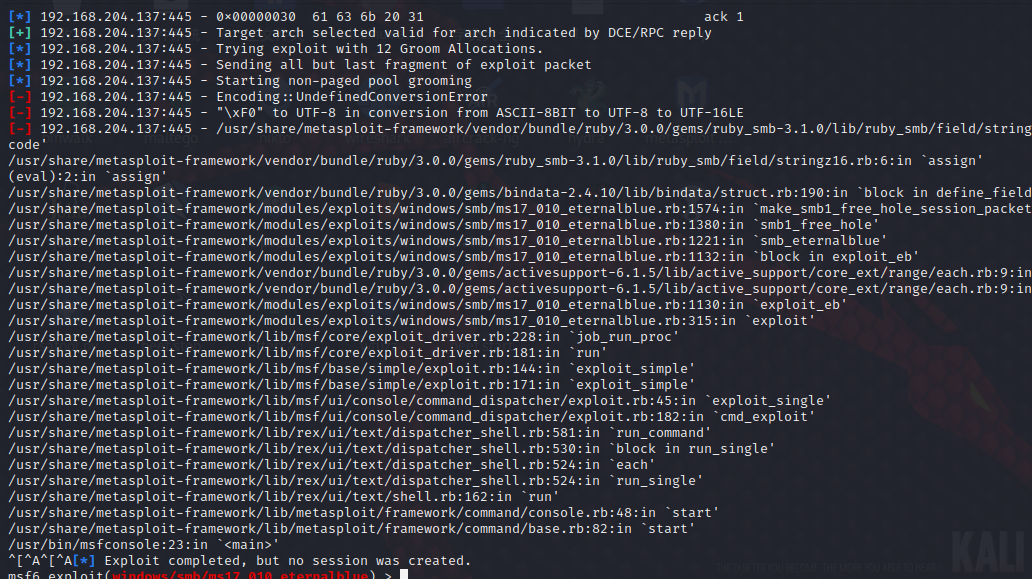
Metasploit (MSF) uses MS17_ 010 (eternal blue) encoding:: undefined conversionerror problem

Registration and skills of hoisting machinery command examination in 2022
![[untitled]](/img/8c/607776e79d66acf9282dca127e12e1.jpg)
[untitled]
随机推荐
openresty ngx_lua请求响应
Ultrasonic sensor flash | LEGO eV3 Teaching
Solve the problem of "no input file specified" when ThinkPHP starts
Realize reverse proxy client IP transparent transmission
如何快速理解复杂业务,系统思考问题?
APK加固技术的演变,APK加固技术和不足之处
Exponential weighted average and its deviation elimination
npm ELECTRON_ Mirror is set as domestic source (npmmirror China mirror)
I closed the open source project alinesno cloud service
Global and Chinese markets for reciprocating seal compressors 2022-2028: Research Report on technology, participants, trends, market size and share
透彻理解JVM类加载子系统
Global and Chinese markets for welding products 2022-2028: Research Report on technology, participants, trends, market size and share
【Note17】PECI(Platform Environment Control Interface)
Arduino 测量交流电流
Data type, variable declaration, global variable and i/o mapping of PLC programming basis (CoDeSys)
Metasploit (MSF) uses MS17_ 010 (eternal blue) encoding:: undefined conversionerror problem
Event trigger requirements of the function called by the event trigger
Editor extensions in unity
Three.js-01 入门
【Note17】PECI(Platform Environment Control Interface)