当前位置:网站首页>LeetCode+ 81 - 85 单调栈专题
LeetCode+ 81 - 85 单调栈专题
2022-07-04 19:17:00 【小雪菜本菜】
搜索旋转排序数组 II
算法标签:数组、二分查找


参考第 33 题
LeetCode+ 31 - 35 二分专题_小雪菜本菜的博客-CSDN博客
(线性扫描) O(n)
参考题解
LeetCode 81 Search in Rotated Sorted Array II - AcWing
这道题类似于第 33 题,不同点在于这道题里的数组可能包含相同元素。
目前能想到的二分做法的最坏时间复杂度都是 O(n),所以索性就拿线性扫描做了^^
时间复杂度分析:整个数组只扫描一遍,所以时间复杂度是 O(n)
class Solution {
public:
bool search(vector<int>& nums, int target) {
for (auto &v : nums)
if (v == target)
return true;
return false;
}
};与第 33 题的区别是里面可能有重复元素,也就意味着可能会出现第一段的前面和第二段的后面的数可能是一样的

如果没有这样的情况的话,我们是可以二分出来分界点的,为什么可以二分出来分界点呢?
假设没有第一段和后面一段相等,假设没有后面一段,就会有后面的数是严格小于第一段这个数的,这个性质是有二段性的,凡是有二段性的性质就可以把分界点二分出来
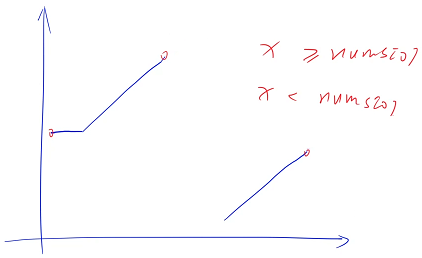
但是这一题没有以上性质,有可能出现后面一段和第一段相等,这一段性质就不成立了
当我们对于一个 x,如果它是大于等于 nums[ 0 ] 的话,并不能确定它是在开头还是在结尾,所以就不能二分了,为了能够让它二分我们可以稍微做一些优化,但是在最坏情况下的时间复杂度还是优化不了

先把开头或者结尾相等的部分删掉就可以了,只有结尾和开头一样,就把结尾删掉,这样就可以二分了
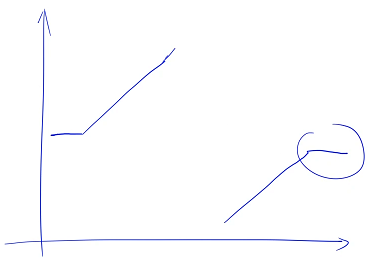
由于删除的这一部分数都是在前面是有重复的,删掉的数都是重复的数,所以并不会影响我们的判断,并不影响答案的准确性,但是我们删完所有重复的数之后,我们就可以二分了,转换为第 33 题求解
题目要求判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ,则返回 true ,否则返回 false 。
思路就是把后面和前面相等的部分先去掉,去掉之后先二分出来分界点,二分出来分界点之后,再在每一段里面二分一下,看它是否存在答案就可以了
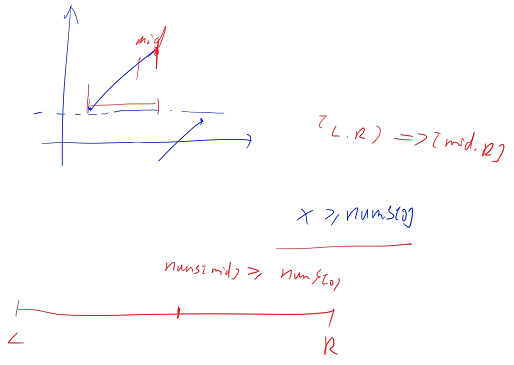
while (R >= 0 && nums[R] == nums[0]) R- -;会执行 n 次,时间复杂度最坏情况下是 O( n )
class Solution {
public:
bool search(vector<int> &nums, int target) {
//数组为空返回 false
if(nums.empty()) return false;
//定义终点
int R = nums.size() - 1;
//当终点大于 0 并且 nums[R] 等于开头的话就可以把这个数删掉
while (R >= 0 && nums[R] == nums[0]) R--;
//如果发现整个数组都被删完了 说明整个数组所有数都一样
if (R < 0)
//由于所有数都一样都等于nums[0],只需要判断nums[0]是不是等于target就可以了
return nums[0] == target;
//把结尾相同的部分删掉 转换为第33题求解
//二分分界点
int l = 0, r = R;
while (l < r) {
int mid = l + r + 1 >> 1;
//如果 nums[mid] 大于等于 nums[0] 说明它在前半段 要二分的分界点其实是满足这个性质的最后一个数
if (nums[mid] >= nums[0]) l = mid;
else r = mid - 1;
}
//得到分界点后判断target属于哪一部分,如果target >= nums[0],说明target是在第一部分,二分的区间应该是从0到刚才的分界点
if (target >= nums[0]) l = 0,r = r;
//否则二分的区间在右半部分 应该是刚才分界点的下一个位置
else l++, r = R;
//最后在l ~ R之间二分找有没有target这个值就可以了
while (l < r) {
int mid = l + r >> 1;
//二分大于等于target的第一个数,如果nums[mid] > = target,说明答案在mid左边或者mid的位置上
if (nums[mid] >= target) r = mid;
else l = mid + 1;
}
//最后判断nums[r]是不是等于target就可以了
return nums[r] == target;
}
};删除排序链表中的重复元素 II
算法标签:链表、双指针
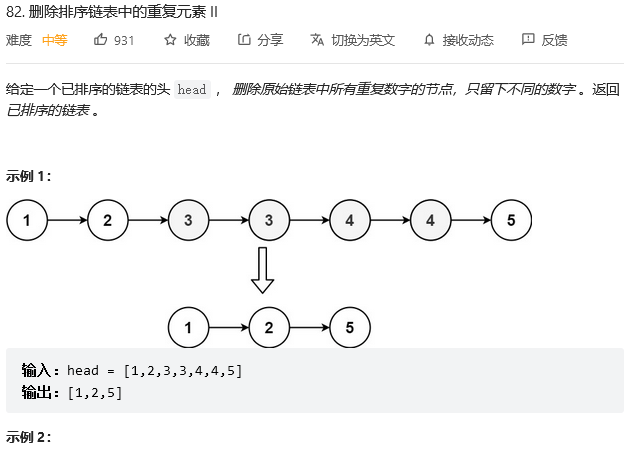
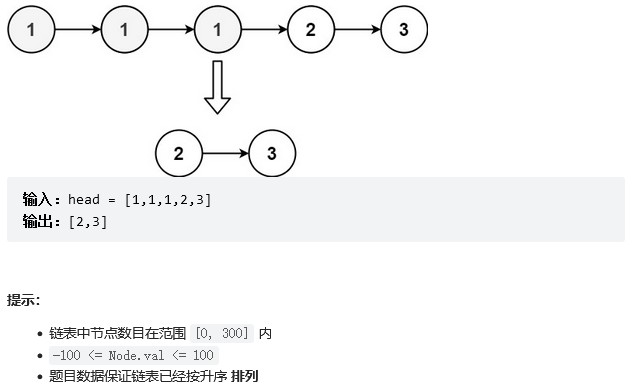
给我们一个排序链表,排序链表意味着所有相同元素是排在一起的,要把里面所有重复的元素删掉,只要有一个元素出现两次及以上就把它删掉,注意不是把有重复的元素删掉只剩下一个
模拟样例
3 有重复,两个 3 都要删掉,类似古代的刑罚 "连坐"
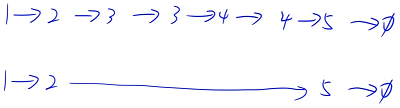
排序链表意味着所有相邻元素是挨在一起的,遍历到某一个点的位置的时候,希望看一下这个点后面连续的相等的一部分的长度是不是大于 1
看后面 4 的个数有几个,如果 4 的个数是大于 1,就需要把后面删掉,如果 4 的个数只有 1 个就不用删除,接下来要做的就是统计一下后面有多少个 4,可以看成是一个双指针算法,把当前连续相等的一段扫描出来,首先用一个指针记录下一段的第一个数是多少,再用一个指针,从下一段的第二个数开始看,只要第二个指针和第一个指针指向的数是一样的,就把第二个指针往后移动一位,直到移动到不相等或者为空为止。当我们移动到 5 的时候发现 5 和 4 不一样,停止移动,这样就可以把这一段相等的区间找出来了
这一段相等的是一个左闭右开的区间,怎么判断当前这一段里面一共有多少个元素呢?
只需要判断第一个指针的下一个位置是不是等于第二个指针就可以了,如果这一段里面只有一个数,第一个指针的下一个位置就是第二个指针的位置,如果这一段里面多余一个数,就意味着第一个指针的下一个位置和第二个指针的位置不相等,这样就可以判断这一段里面有几个元素了
①如果下一段里面只有一个数,只需要把第一个指针往后移动一位就可以了
②如果下一段里面有多于一个数,需要把下一段的数都删掉,把上一个节点的 next 指针直接指向第二个指针就可以了
每次指针指向的应该是某一段的前一个数,头节点前一个数应该也是存在的,为了方便先建立一个虚拟头节点

/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
auto dummy = new ListNode(-1);
//虚拟头节点的 next 指针等于真实的头节点
dummy->next = head;
//定义指向某一段前面的指针
auto p = dummy;
//当有下一段的时候 每次把下一段的第二个找出来
while(p->next) {
auto q = p->next->next;
//当下一段的第二个数是存在的并且下一段的第二个数的值是等于下一段第一个数的值 第二个指针就一直往后走
while(q && q->val == p->next->val) q = q->next;
//如果第一个指针的 next 如果是等于 q 的话,说明下一段只有一个数
if(p->next->next == q)
//p 走到下一个位置就可以了
p = p->next;
//否则把下一段删掉
else p->next = q;
}
//返回虚拟头节点的下一个位置
return dummy->next;
}
};删除排序链表中的重复元素
算法标签:链表
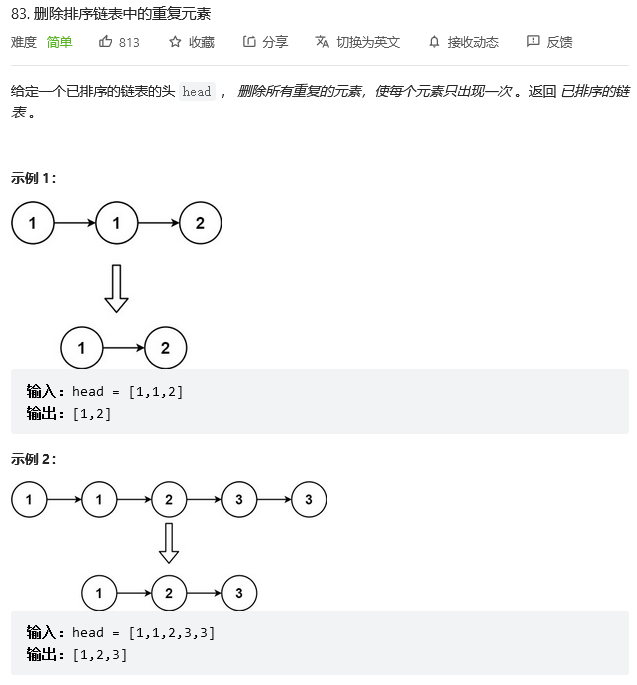

由于链表是排序的,说明所有相同的元素排在一起

对于某一段相同的数,为了只保留一项,我们规定每一项相同的数保留第一项
模拟样例
有很多 2,只选择第一个 2,有很多 3,只选择第一个 3 ,接下来看一下怎么去把每一段的第一个数存储下来。首先,整个链表的第一个数一定会被存储下来,因为它一定是某一段的第一个数,第一个数存储下来之后,再从整个链表的第二个数开始遍历,每次判断当前遍历的这个数是不是这一段的第一个数,如果是这一段的第一个数的话,就把这个节点挪过来,如果不是的话就跳过
怎么判断当前这个数是不是这一段的第一个数呢?
只需要看一下当前这个数和我们存储的链表的最后一个数是不是一样就可以了,可以发现 2 != 1,所以这个 2 一定是第一个 2,把这个 2 挪过来,再继续往后看下一个数 2 == 2,说明 2 已经存在了,直接跳过。接下来看 3,由于 3 != 2,所以这个 3 是第一个 3,把这个 3 挪过来,以此类推,最后补上一个空指针就可以了
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
//为空 返回空
if(!head) return head;
//用cur表示新链表的最后一个节点
auto cur = head;
//从原链表的第二个点开始遍历
for(auto p = head->next; p; p = p->next)
//每次比较当前节点和新链表的最后一个节点是不是一样
if(p->val != cur->val)
//如果不一样就把当前这个点移到新链表cur的最后 p是新链表的最后一个点
cur = cur->next = p;
//最后将新链表的尾节点指向空
cur->next = NULL;
//返回新链表
return head;
}
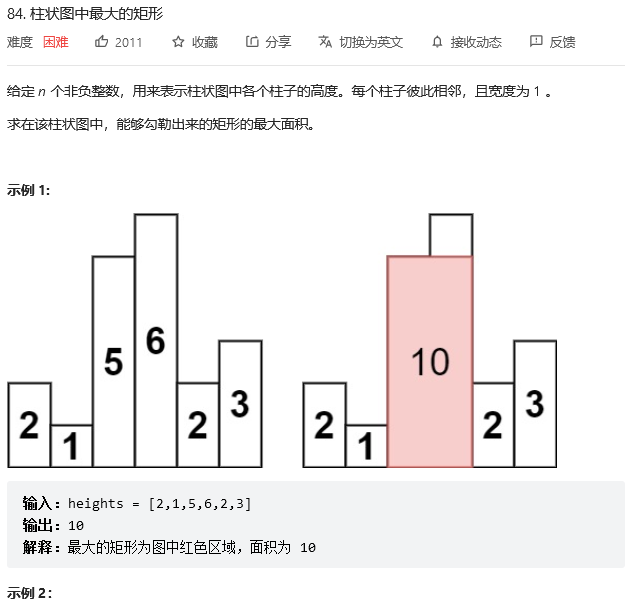
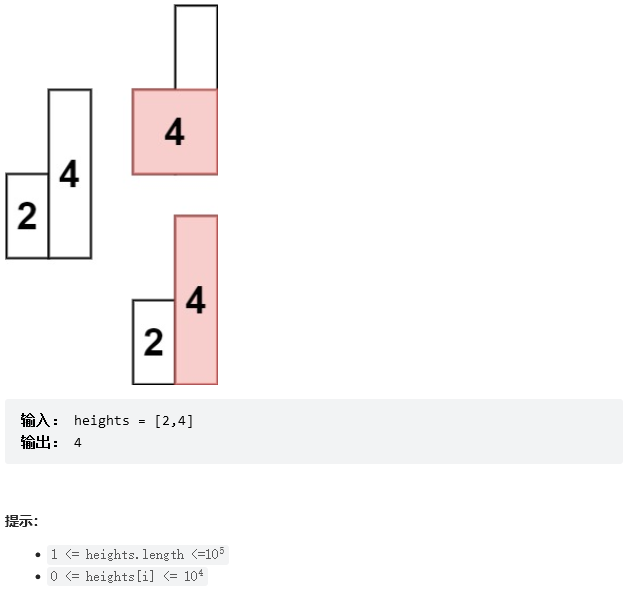
};柱状图中最大的矩形
算法标签:栈、数组、单调栈
单调栈的经典应用
链表与邻接表、栈与队列、单调栈、单调队列、kmp 算法_小雪菜本菜的博客-CSDN博客
单调栈能解决找一个序列里面每一个数左边离它最近的那个比它小的数的下标是多少,接下来看一些题目里面有没有这样的模型
题目给出 n 个竖条,这 n 个竖条的宽度都是 1,高度是给定的,n 个竖条坐落在一个坐标轴上,两两之间紧挨在一起,我们需要找到这个竖条里面积最大的矩形是多少?
这道题目其实是枚举加优化的问题,接下来想一下怎么把所有的情况枚举出来,枚举的时候可以枚举很多东西,可以枚举矩形的左右边界,需要两重循环,时间复杂度为 O(n^2),在左右边界确定的情况下,看高度最大是多少
我们也可以考虑枚举矩形的上边界,矩形的上边界一定是被某一条竖线卡住的,不可能在竖线的中间的位置,例如我们想看一下以 5 这条边为上边界的矩形,左右宽度最大是多少 → 向左最大是多少?向右最大是多少?
左右边界就是看这条竖线的左右两边第一个比它矮的矩形的位置
面积就是上边界的高度乘以左右边界的距离
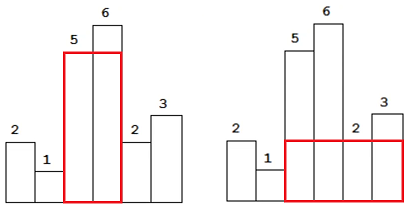
我们可以枚举上边界,当我们枚举完上边界之后,只需要求一下对于每一个上边界来说,以这个边为上边界的话,往左数最远到什么地方?以及往右数最远到什么地方?
往左数最远到什么地方其实就是求一下这个竖条左边离它最近的那个比它矮的柱子在什么位置就可以了
往右数最远到什么地方其实就是求一下这个竖条右边离它最近的那个比它矮的柱子在什么位置就可以了
然后就可以求出来最大面积
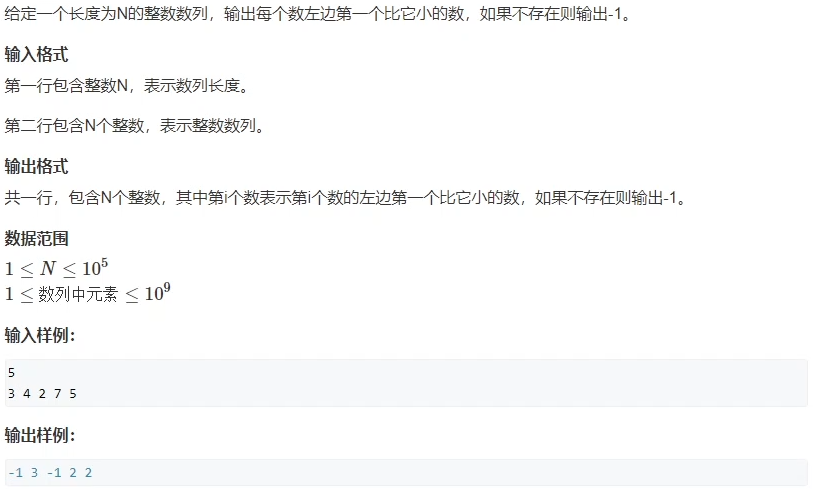
本质上是找到每个数左边第一个比它小的数的位置,以及每个数右边第一个比它小的数的位置
先从左往右扫描一遍找到左边第一个比它小的,然后从右往左扫描一遍,找到右边第一个比它小的就可以了
怎么用单调栈求每个数左边第一个比它小的数?
从左往右扫描的时候,把所有数记录到栈里面,横坐标是它的下标,纵坐标是数的大小,每次对于当前这个数怎么找到这个数左边第一个比它小的数呢?我们从栈顶开始扫描,直到扫描到第一个比它小的数为止

优化
右边是栈顶,左边是栈底,假设左边的数 ① 比右边的数 ② 大,如果有一个数比 ① 大的话就一定比 ② 大,而且 ② 在 ① 的右边,只要 ② 存在,① 就一定不会被用到,就可以把 ① 删掉,只要前一个数比后一个数大,就可以把前面的一个数删掉,这样删完之后,这个栈就变成单调栈
对于当前这个数,找比这个数小的第一个数的时候,我们可以从栈顶开始找,只要栈顶元素比当前这个数大就说明栈顶元素没有用,栈顶元素就可以删掉,直到栈顶元素比当前元素小为止,把当前这个数加到栈里面,加之前,这个栈顶就是当前这个数要找的数

时间复杂度分析
每个数只会进栈一次,而且只会出栈一次,所以整个做法的时间复杂度是 O(n)
class Solution {
public:
int largestRectangleArea(vector<int>& h) {
//用 n 表示最大长度
int n = h.size();
//定义每个数左边第一个比它小的数的位置、每个数右边第一个比它小的数的位置
vector<int> left(n),right(n);
//定义一个栈
stack<int> stk;
//从前往后扫描一下每个数
for(int i = 0; i < n;i ++ ) {
//当栈里面是有元素的 并且栈顶元素大于等于当前元素的话 就把栈顶元素删掉
while(stk.size() && h[stk.top()] >= h[i]) stk.pop();
//如果栈里面为空,说明任何一个数都比当前这个数大,左边界可以取最左边这条边,把它赋值为-1
if(stk.empty()) left[i] = -1;
//否则left[i]等于栈顶元素的下标
else left[i] = stk.top();
//把当前元素插到栈里面
stk.push(i);
}
//把栈清空
stk = stack<int>();
//从后往左扫描一下每个数
for(int i = n - 1; i >= 0; i-- ) {
//当栈里面是有元素的 并且栈顶元素大于等于当前元素的话 就把栈顶元素删掉
while(stk.size() && h[stk.top()] >= h[i]) stk.pop();
//如果栈里面为空
if(stk.empty()) right[i] = n;
//否则right[i]等于栈顶元素的下标
else right[i] = stk.top();
//把当前元素插到栈里面
stk.push(i);
}
//遍历每一个上边界 更新答案
int res = 0;
//结合边界情况理解
for(int i = 0; i < n; i++ ) {
res = max(res,h[i] * (right[i] - left[i] - 1));
cout << "h[" << i << "]:"<< h[i] << "\t" << "l[" << i
<< "]:" << left[i] << "\t" << "r[" << i << "]:" << right[i] << "\t";
}
return res;
}
};
stdout
h[0]:2 l[0]:-1 r[0]:1 h[1]:1 l[1]:-1 r[1]:6 h[2]:5 l[2]:1 r[2]:4
h[3]:6 l[3]:2 r[3]:4 h[4]:2 l[4]:1 r[4]:6 h[5]:3 l[5]:4 r[5]:6 最大矩形
算法标签:栈、数组、动态规划、矩阵、单调栈
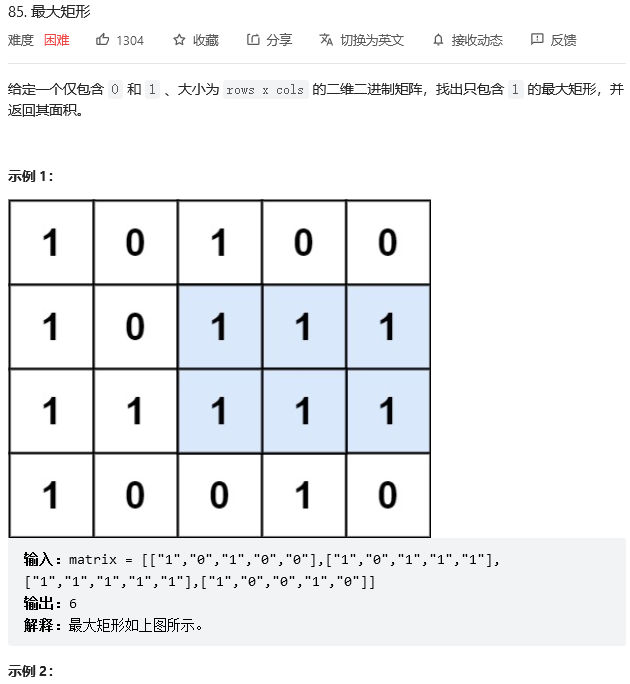

给我们一个 0、1 矩阵,要在这个 0、1 矩阵里面找到一个最大的只包含 1 的矩形,需要考虑怎么枚举所有方案,最坏情况可以先枚举左上角的坐标再枚举右下角坐标,然后再判断矩形里面是不是全是 1,时间复杂度是 O(n^6),判断矩形里面是不是全是 1 可以用前缀和优化,时间复杂度为 O(n^4)
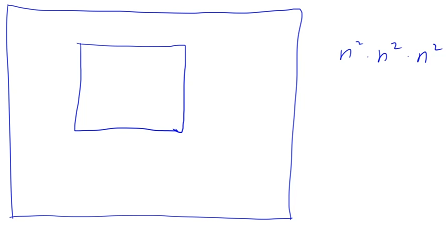
上一题是给我们一堆柱子,在柱子里面找到一个最大的矩形,这一题是考虑怎么找到那一堆柱子
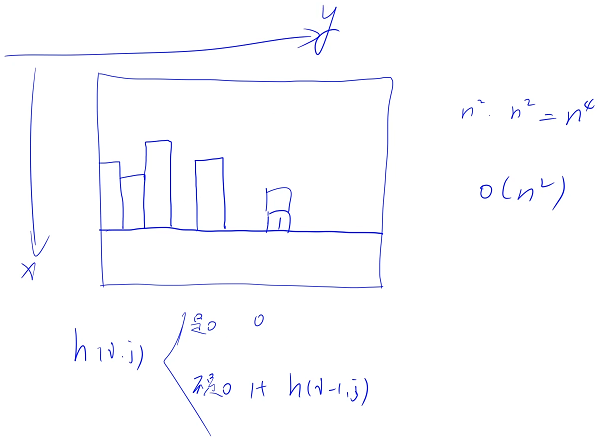
借助上一题的模型,先枚举要枚举矩形的下边界,再预处理一下每个格子往上数最多有多少个连续的 1,注意这是最大的高度,上面全是 0,柱子全是 1,当然也存在柱子高度是 0 的情况
当下边界确定之后,要在这一堆柱子里面找到一个最大的矩形,只要把这一堆柱子找出来,就可以在 O(n) 的时间内,求出来所有下边界是这条线的、全是 1 的矩形里面、面积最大的矩形是多少?枚举矩形下边界需要 O(n) 的时间,所以整个算法的时间复杂度是 O(n^2)
怎么预处理出来每一个位置往上数,最多有多少个连续的 1 呢?可以递推一下
用 f(i,j) 表示 (i,j) 这个格子往上数、最多有多少个连续的 1,有两种情况
①(i,j) 这个格子是 0 的话,那么 f(i,j) 就是 0
②(i,j) 这个格子不是 0 的话,那么 f(i,j) 就是 1 +(i - 1,j) 这个格子往上数最多有多少个矩形 f(i - 1,j)
class Solution {
public:
int largestRectangleArea(vector<int>& h) {
//最大长度
int n = h.size();
//定义每个数左边第一个比它小的数的位置、每个数右边第一个比它小的数的位置
vector<int> left(n),right(n);
//定义一个栈
stack<int> stk;
//从前往后扫描一下每个数
for(int i = 0; i < n;i ++ ) {
//当栈里面是有元素的 并且栈顶元素大于等于当前元素的话 就把栈顶元素删掉
while(stk.size() && h[stk.top()] >= h[i]) stk.pop();
//如果栈里面为空,说明任何一个数都比当前这个数大,左边界可以取最左边这条边,把它赋值为-1
if(stk.empty()) left[i] = -1;
//否则left[i]等于栈顶元素的下标
else left[i] = stk.top();
//把当前元素插到栈里面
stk.push(i);
}
//把栈清空
stk = stack<int>();
//从后往左扫描一下每个数
for(int i = n - 1; i >= 0; i-- ) {
//当栈里面是有元素的 并且栈顶元素大于等于当前元素的话 就把栈顶元素删掉
while(stk.size() && h[stk.top()] >= h[i]) stk.pop();
//如果栈里面为空
if(stk.empty()) right[i] = n;
//否则right[i]等于栈顶元素的下标
else right[i] = stk.top();
//把当前元素插到栈里面
stk.push(i);
}
//遍历每一个上边界 更新答案
int res = 0;
for(int i = 0; i < n; i++ ) res = max(res,h[i] * (right[i] - left[i] - 1));
return res;
}
int maximalRectangle(vector<vector<char>>& matrix) {
//为空返回0
if(matrix.empty() || matrix[0].empty()) return 0;
//用 n 表示高度 用 m 表示宽度
int n = matrix.size(),m = matrix[0].size();
//用二维数组h表示每个数上面最多有多少个连续的1
vector<vector<int>> h(n,vector<int>(m));
//求 h(i,j)
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++) {
//matrix[i][j]!='0'
if(matrix[i][j] == '1') {
//如果i>0 递推
if(i) h[i][j] = 1 + h[i - 1][j];
else h[i][j] = 1;
}
}
int res = 0;
//枚举下边界
for(int i = 0;i < n; i++ ) res = max(res,largestRectangleArea(h[i]));
return res;
}
};边栏推荐
- What financial products can you buy with a deposit of 100000 yuan?
- 九齐单片机NY8B062D单按键控制4种LED状态
- js 闭包
- What if the WiFi of win11 system always drops? Solution of WiFi total drop in win11 system
- Flet教程之 06 TextButton基础入门(教程含源码)
- How to solve the problem that win11 cannot write the value to the registry key?
- 最长的可整合子数组的长度
- 电脑页面不能全屏怎么办?Win11页面不能全屏的解决方法
- LeetCode 871. Minimum refueling times
- 看腾讯大老如何做接口自动化测试
猜你喜欢
See how Tencent does interface automation testing
How does the computer save web pages to the desktop for use
强化学习-学习笔记2 | 价值学习
Win11U盘拒绝访问怎么办?Win11U盘拒绝访问的有效解决方法
How to solve the problem that win11 cannot write the value to the registry key?
一文搞懂Go语言中文件的读写与创建
AP8022开关电源小家电ACDC芯片离线式开关电源IC
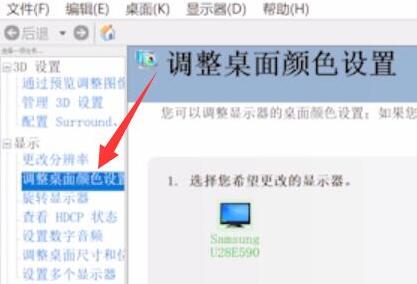
What if the brightness of win11 is locked? Solution to win11 brightness locking
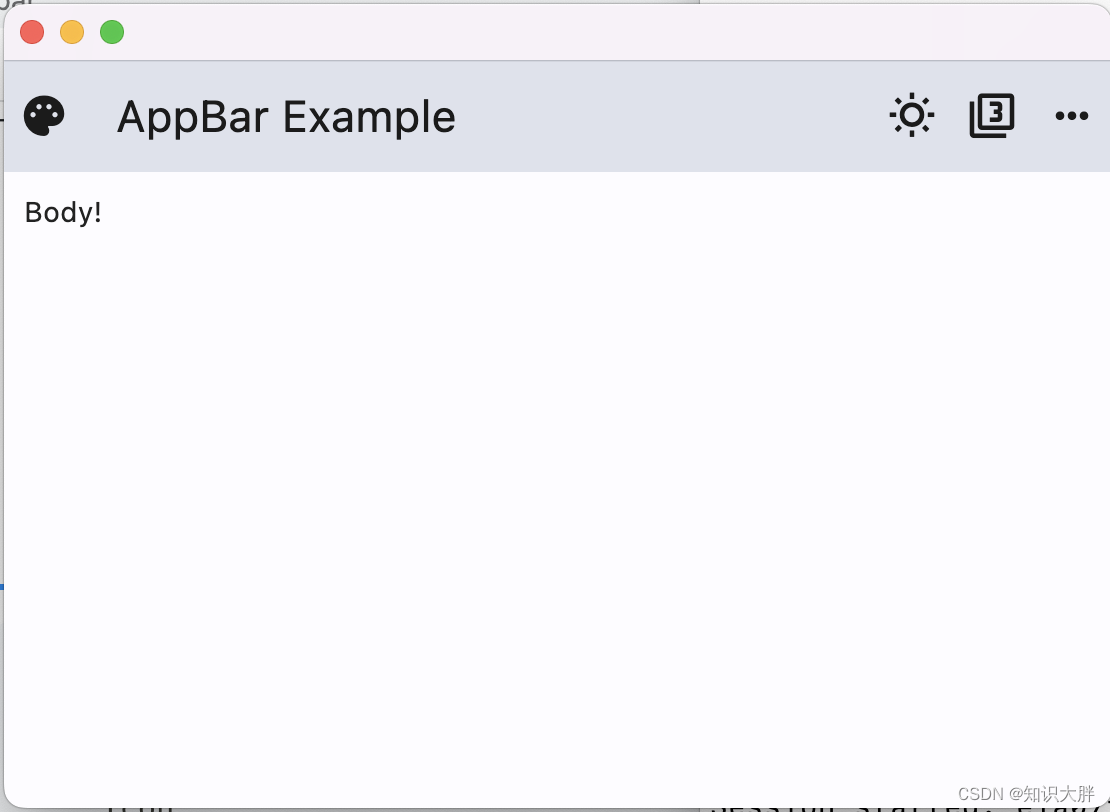
Flet教程之 08 AppBar工具栏基础入门(教程含源码)
FS4061A升压8.4V充电IC芯片和FS4061B升压12.6V充电IC芯片规格书datasheet
随机推荐
In operation (i.e. included in) usage of SSRs filter
Six stones programming: about code, there are six triumphs
分析伦敦银走势图的技巧
Play the music of youth
Automatic generation of interface automatic test cases by actual operation
Flet tutorial 05 outlinedbutton basic introduction (tutorial includes source code)
Four traversal methods of binary tree, as well as the creation of binary tree from middle order to post order, pre order to middle order, pre order to post order, and sequence [specially created for t
LeetCode 871. Minimum refueling times
Flet tutorial 06 basic introduction to textbutton (tutorial includes source code)
左右最值最大差问题
Flet教程之 07 PopupMenuButton基础入门(教程含源码)
太方便了,钉钉上就可完成代码发布审批啦!
Is it safe for Great Wall Securities to open an account? Stock account opening process online account opening
Lingyun going to sea | 10 jump &huawei cloud: jointly help Africa's inclusive financial services
九齐单片机NY8B062D单按键控制4种LED状态
Dynamic memory management
How to solve the problem that win11 cannot write the value to the registry key?
Summary of the mistakes in the use of qpainter in QT gobang man-machine game
MySQL statement execution details
What if the win11 shared file cannot be opened? The solution of win11 shared file cannot be opened