当前位置:网站首页>OFDM 十六讲 5 -Discrete Convolution, ISI and ICI on DMT/OFDM Systems
OFDM 十六讲 5 -Discrete Convolution, ISI and ICI on DMT/OFDM Systems
2022-08-05 05:09:00 【明朝百晓生】
参考:

这篇文章的观点非常新颖和直观,主要从线性代数方面阐述相关原理
目录:
1: 离散卷积
2: ISI & ICI
一 离散卷积
前面讲过连续数据的卷积公式

实际没有连续的数据我们一般采用离散卷积,
![y(k)=\sum_{0}^{\infty} x[n] \bullet h[k-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_21.gif)
假设x的长度为n, h的长度为m, y的长度为n+m
1.1 例子
假设
![x=[x_0,x_1,x_2,x_3]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_19.gif)
![h=[h_0,h_1,h_2,h_3]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_15.gif)
![y_0=\sum_{n=0}^{3}x[n]\bullet h[0-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_0.gif)

![y_1=\sum_{n=0}^{3}x[n]\bullet h[1-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_6.gif)

![y_2=\sum_{n=0}^{3}x[n]\bullet h[2-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_23.gif)

![y_3=\sum_{n=0}^{3}x[n]\bullet h[3-n]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_28.gif)

本质上就是两个矩阵相乘
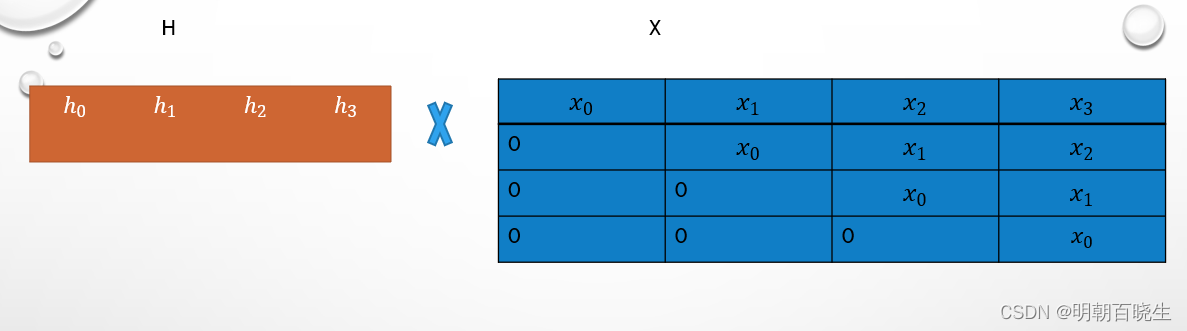
进一步表示方法,如下图,为对应列元素相乘后求和

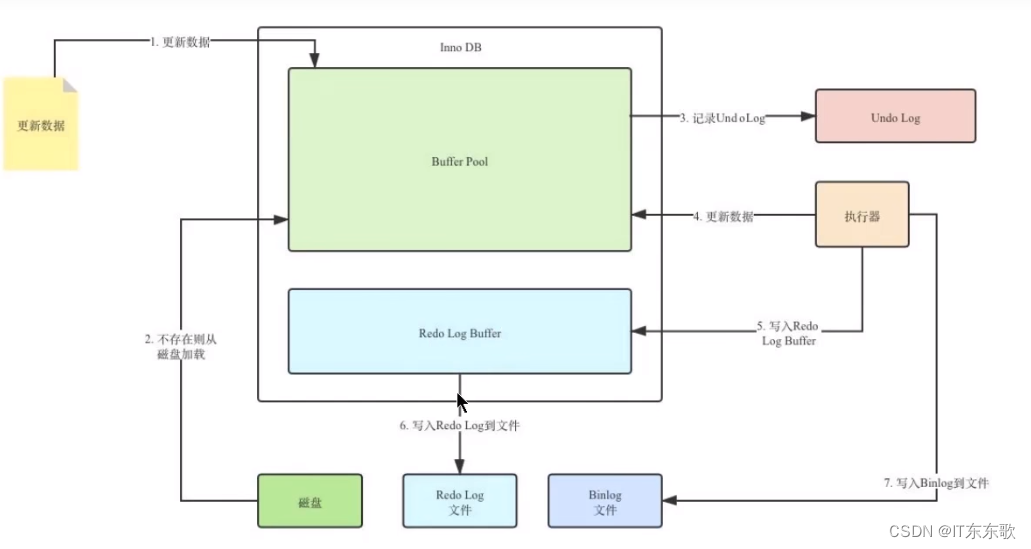
二 CP(Cyclic prefix) CS(Cyclic suffix)
2.1 循环前缀,循环后缀结构

发送端
经过IDFT 离散傅里叶逆变换后,得到长度为N的时域数据
然后插入长度为a 的cp, 以及长度为b 的 cs

假设原始数据为
![X=[x_0,x_1,x_2,x_3]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_18.gif)
a= b=2
![cp=[x_2,x_3], cs=[x_0,x_1]](http://img.inotgo.com/imagesLocal/202208/05/202208050509096410_8.gif)
最后数据变成了

2.2 ICI
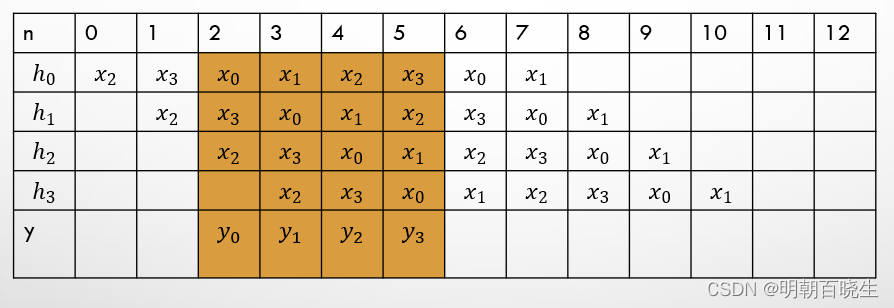
译码的时候,我们会对其做傅里叶变换,对CP,CS 部分丢弃

如下

发现了多了一个噪声 

 ,其它信道之间的干扰
,其它信道之间的干扰
下面是草图

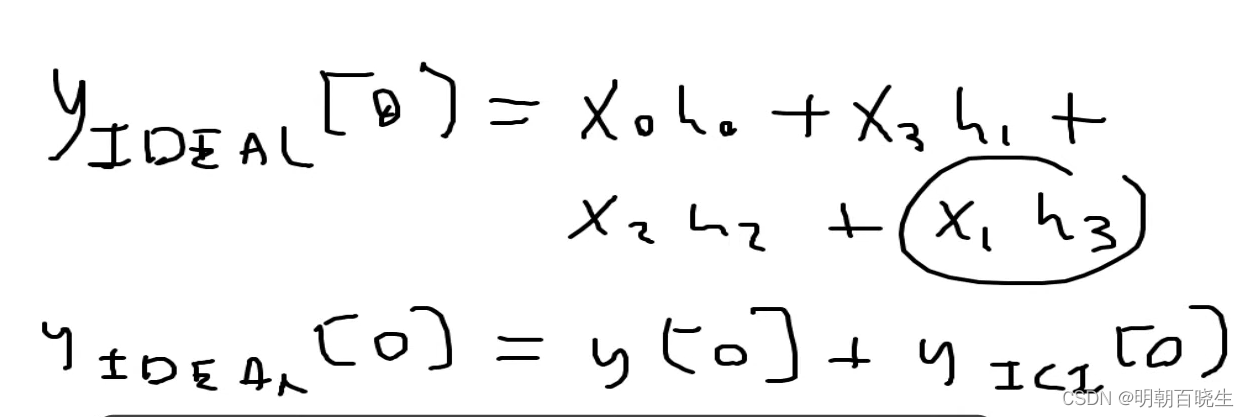
2.3 ISI 模型
跟上面差不多

,
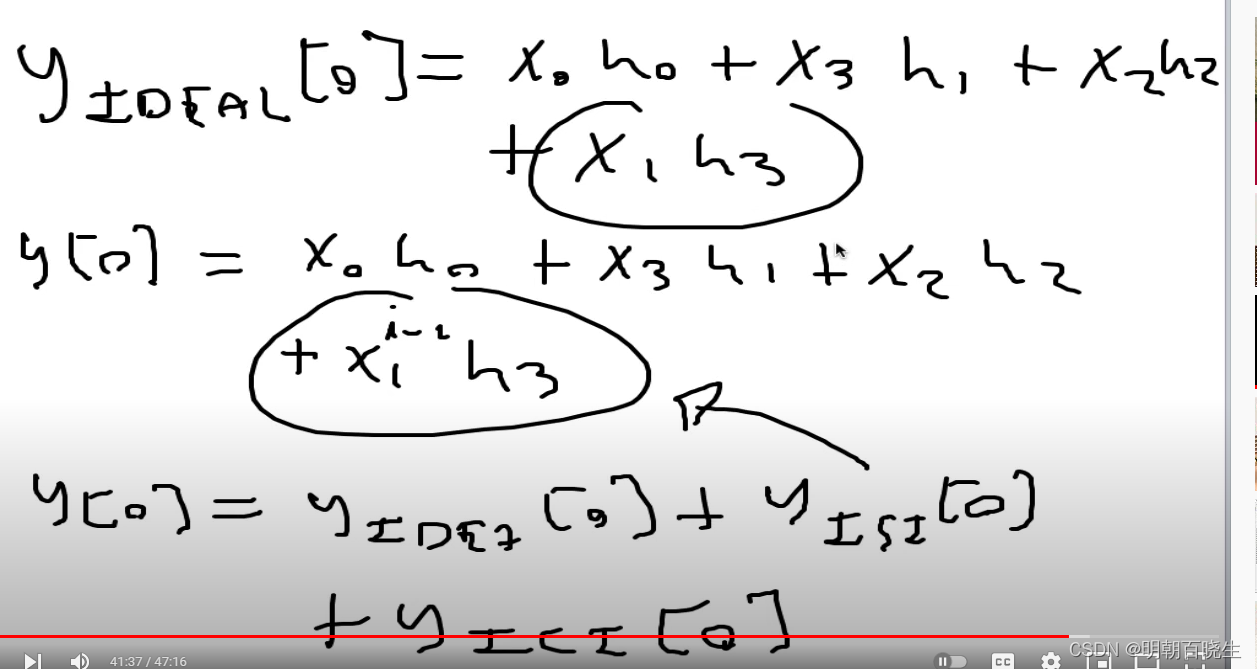
边栏推荐
猜你喜欢
随机推荐
uva1325
LAB 信号量实现细节
电话溥功能
Please write the SparkSQL statement
二叉树基本性质+oj题解析
mutillidae download and installation
jvm 三 之堆与栈
C++ core programming
WPF中DataContext作用
UVA10827
How to identify false evidence and evidence?
The role of DataContext in WPF
Application status of digital twin technology in power system
Mvi架构浅析
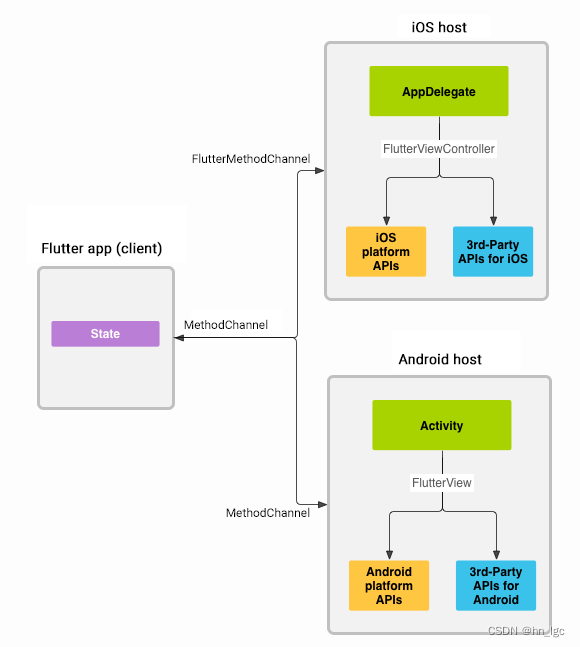
How does the Flutter TapGestureRecognizer work
数字孪生技术在电力系统中的应用现状
how to measure distance from point to face in creo
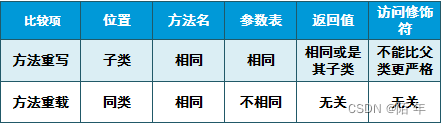
Day019 方法重写与相关类的介绍
[Nine Lectures on Backpacks - 01 Backpack Problems]
Detailed explanation of each module of ansible