当前位置:网站首页>[Nine Lectures on Backpacks - 01 Backpack Problems]
[Nine Lectures on Backpacks - 01 Backpack Problems]
2022-08-05 04:21:00 【romantic dog】
更好的阅读体验 \color{red}{更好的阅读体验} 更好的阅读体验
1. 01背包问题
1.1 模板题
01背包问题
描述
有 N 件物品和一个容量是 V 的背包.每件物品只能使用一次.
第 i 件物品的体积是 vi,价值是 wi.
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大.
输出最大价值.
输入格式
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积.
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值.
输出格式
输出一个整数,表示最大价值.
数据范围
0<N,V≤1000
0<vi,wi≤1000
4 5
1 2
2 4
3 4
4 5
输出样例:
输出样例:
8
思想
- 状态表示:
- 集合:
dp[i][j]表示前i个物品,总体积不超过j的价值 - 属性:最大价值
- 集合:
- 状态计算:
- 不选第
i个 物品:dp[i][j] = dp[i - 1][j] - 选第
i个物品:dp[i][j] = dp[i - 1][j - v[i]] + w[i] - The collection property is the maximum value,So take two cases
max()
- 不选第
- When the backpack capacity is not enough,即
j < v[i]时,Items cannot be selected,Otherwise optional
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int dp[N][N];
int v[N], w[N];
void solve(){
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++){
for(int j = 0; j <= m; j ++){
dp[i][j] = dp[i - 1][j]; //不选物品i
if(j >= v[i]) dp[i][j] = max(dp[i][j],dp[i - 1][j - v[i]] + w[i]); //选择物品i
}
}
cout << dp[n][m] << endl;
}
int main(){
solve();
return 0;
}
优化
- 对于
dp[i][j]All are recordedi个物品在j容量下的最大价值,但我们只需要dp[n][m],故只需要dp[j] - 对于
dp[i][j]的更新,dp[i][j] = max(dp[i][j],dp[i - 1][j - v[i]] + w[i]),when the first dimensioniafter being omitted,Ambiguity arises when updating - 故更新
dp[j]需要从j = m到j = v[i]逆序,避免歧义 - 状态表示:
- 集合:
dp[j]为 N N N件物品,容量为j的价值 - 属性:最大价值
- 集合:
- 状态计算:
dp[j] = max(dp[j],dp[j - v[i]] + w[i])
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 10;
int dp[N];
int v[N], w[N];
void solve(){
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i ++){
for(int j = m; j >= v[i]; j --){
dp[j] = max(dp[j],dp[j - v[i]] + w[i]);
}
}
cout << dp[m] << endl;
}
int main(){
solve();
return 0;
}
1.2 提高练习
426. 开心的金明
描述
金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间.
更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说了算,只要不超过 N 元钱就行”.
今天一早金明就开始做预算,但是他想买的东西太多了,肯定会超过妈妈限定的 N 元.
于是,他把每件物品规定了一个重要度,分为 5 等:用整数 1∼5 表示,第 5 等最重要.
他还从因特网上查到了每件物品的价格(都是整数元).
他希望在不超过 N 元(可以等于 N 元)的前提下,使每件物品的价格与重要度的乘积的总和最大.
设第 j 件物品的价格为 v[j],重要度为 w[j],共选中了 k 件物品,编号依次为 j1,j2,…,jk,则所求的总和为:
v[j1]×w[j1]+v[j2]×w[j2]+…+v[jk]×w[jk]
请你帮助金明设计一个满足要求的购物单.
输入格式
输入文件的第 1 行,为两个正整数 N 和 m,用一个空格隔开.(其中 N 表示总钱数,m 为希望购买物品的个数)
从第 2 行到第 m+1 行,第 j 行给出了编号为 j−1 的物品的基本数据,每行有 2 个非负整数 v 和 p.(其中 v 表示该物品的价格,p 表示该物品的重要度)
输出格式
输出文件只有一个正整数,为不超过总钱数的物品的价格与重要度乘积的总和的最大值(数据保证结果不超过 108).
数据范围
1≤N<30000,
1≤m<25,
0≤v≤10000,
1≤p≤5
输入样例:
1000 5
800 2
400 5
300 5
400 3
200 2
输出样例:
3900
思想
- 01背包模板题
- Think of the product of priority and cost as a value
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int dp[N];
int v[N], w[N];
void solve(){
int n, m;
cin >> m >> n;
for(int i = 1; i <= n; i ++){
cin >> v[i] >> w[i];
w[i] *= v[i];
}
for(int i = 1; i <= n; i ++){
for(int j = m; j >= v[i]; j --){
dp[j] = max(dp[j],dp[j - v[i]] + w[i]);
}
}
cout << dp[m] << endl;
}
int main(){
solve();
return 0;
}
1024. 装箱问题
描述
有一个箱子容量为 V,同时有 n 个物品,每个物品有一个体积(正整数).
要求 n 个物品中,任取若干个装入箱内,使箱子的剩余空间为最小.
输入格式
第一行是一个整数 V,表示箱子容量.
第二行是一个整数 n,表示物品数.
接下来 n 行,每行一个正整数(不超过10000),分别表示这 n 个物品的各自体积.
输出格式
一个整数,表示箱子剩余空间.
数据范围
0<V≤20000,
0<n≤30
输入样例:
24
6
8
3
12
7
9
7
输出样例:
0
思想
- Treat the value of an item as equal to its volume,转化为01背包问题
- That is, the value attached to the selected item is equal to the volume occupied by the selected item
- 状态表示:
- 集合:
dp[j]表示体积不超过j时,Volume used - 属性:Maximum use volume
- 集合:
- 状态计算:
dp[j] = max(dp[j],dp[j - v[i]] + v[i])
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int dp[N];
int v[N];
void solve(){
int n, m;
cin >> m >> n;
for(int i = 1; i <= n; i ++) cin >> v[i];
for(int i = 1; i <= n; i ++){
for(int j = m; j >= v[i]; j --){
dp[j] = max(dp[j],dp[j - v[i]] + v[i]);
}
}
cout << m - dp[m] << endl;
}
int main(){
solve();
return 0;
}
278. 数字组合
描述
给定 N 个正整数 A1,A2,…,AN,从中选出若干个数,使它们的和为 M,求有多少种选择方案.
输入格式
第一行包含两个整数 N 和 M.
第二行包含 N 个整数,表示 A1,A2,…,AN.
输出格式
包含一个整数,表示可选方案数.
数据范围
1≤N≤100,
1≤M≤10000,
1≤Ai≤1000,
答案保证在 int 范围内.
输入样例:
4 4
1 1 2 2
输出样例:
3
思想
- 状态表示:
- 集合:
dp[i][j]表示前iThe sum of the selected numbers is exactly equal toj的集合 - 属性:集合的个数
- 集合:
- 状态计算:
- 不选第
i个数:dp[i][j] = dp[i][j] - 选第
i个数:dp[i][j] = dp[i - 1][j - v[i]] - 初始化:
dp[0][0] = 1,j = 0Not choosing is a solution - The collection property is the number of collections,Take the sum of the two options:
dp[i][j] += dp[i - 1][j - v[i]] - 优化:
dp[j] += dp[j - v[i]]
- 不选第
代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 3;
int dp[N];
int v[N];
void solve(){
int n, m;
cin >> n >> m;
dp[0] = 1;
for(int i = 1; i <= n; i ++){
cin >> v[i];
}
for(int i = 1; i <= n; i ++){
for(int j = m; j >= v[i]; j --){
dp[j] += dp[j - v[i]];
}
}
cout << dp[m] << endl;
}
int main(){
solve();
return 0;
}
734. 能量石
描述
岩石怪物杜达生活在魔法森林中,他在午餐时收集了 N 块能量石准备开吃.
由于他的嘴很小,所以一次只能吃一块能量石.
能量石很硬,吃完需要花不少时间.
吃完第 i 块能量石需要花费的时间为 Si 秒.
杜达靠吃能量石来获取能量.
不同的能量石包含的能量可能不同.
此外,能量石会随着时间流逝逐渐失去能量.
第 i 块能量石最初包含 Ei 单位的能量,并且每秒将失去 Li 单位的能量.
当杜达开始吃一块能量石时,他就会立即获得该能量石所含的全部能量(无论实际吃完该石头需要多少时间).
能量石中包含的能量最多降低至 0.
请问杜达通过吃能量石可以获得的最大能量是多少?
输入格式
第一行包含整数 T,表示共有 T 组测试数据.
每组数据第一行包含整数 N,表示能量石的数量.
接下来 N 行,每行包含三个整数 Si,Ei,Li.
输出格式
每组数据输出一个结果,每个结果占一行.
结果表示为 Case #x: y,其中 x 是组别编号(从 1 开始),y 是可以获得的最大能量值.
数据范围
1≤T≤10,
1≤N≤100,
1≤Si≤100,
1≤Ei≤105,
0≤Li≤105
输入样例:
3
4
20 10 1
5 30 5
100 30 1
5 80 60
3
10 4 1000
10 3 1000
10 8 1000
2
12 300 50
5 200 0
输出样例:
Case #1: 105
Case #2: 8
Case #3: 500
思想
贪心 + 01背包
For two adjacent power stones i , j i,j i,j
E i + E j − S i × L j ≥ E j + E i − S j × L i S j × L i ≥ S i × L j E_i+E_j−S_i×L_j \ge E_j+E_i−S_j×L_i\\\\ S_j×L_i\ge S_i×L_j Ei+Ej−Si×Lj≥Ej+Ei−Sj×LiSj×Li≥Si×Lj
So for all the optimal solutions S j × L i < S i × L j S_j×L_i \lt S_i×L_j Sj×Li<Si×Ljorder of items,We can all pass once邻项交换The operation becomes our above sequence,And ensure that the exchange is completed,The total value does not decrease
代码
#include <bits/stdc++.h>
using namespace std;
int _, __;
const int N = 110;
struct point{
int s, e, l;
bool operator < (const point &p) const{
return s * p.l < p.s * l;
}
};
void solve(){
int dp[N * N] = {
0};
point p[N];
int n;
cin >> n;
int m = 0;
for(int i = 1; i <= n; i++) {
cin >> p[i].s >> p[i].e >> p[i].l;
m += p[i].s;
}
sort(p + 1, p + 1 + n);
for(int i = 1; i <= n; i++) {
for(int j = m; j >= p[i].s; j--){
dp[j] = max(dp[j], dp[j - p[i].s] + max(0, p[i].e - (j - p[i].s) * p[i].l));
}
}
int res = 0;
for(int i = 1; i <= m; i++) res = max(res, dp[i]);
printf("Case #%d: %d\n", __, res);
}
int main(){
int _;
cin >> _;
for(__ = 1; __ <= _; __ ++){
solve();
}
return 0;
}
边栏推荐
- How do newcomers get started and learn software testing?
- 银行数据采集,数据补录与指标管理3大问题如何解决?
- 【8.2】代码源 - 【货币系统】【硬币】【新年的问题(数据加强版)】【三段式】
- UE4 第一人称角色模板 添加生命值和调试伤害
- 狗仔队:表面编辑多视点图像处理
- token, jwt, oauth2, session parsing
- 阿里本地生活单季营收106亿,大文娱营收72亿,菜鸟营收121亿
- DEJA_VU3D - Cesium功能集 之 059-腾讯地图纠偏
- 36-Jenkins-Job Migration
- 【informix】解决启动报错大全,以及解决办法
猜你喜欢
炎炎夏日教你利用小米智能家居配件+树莓派4接入Apple HomeKit
About the installation of sklearn library
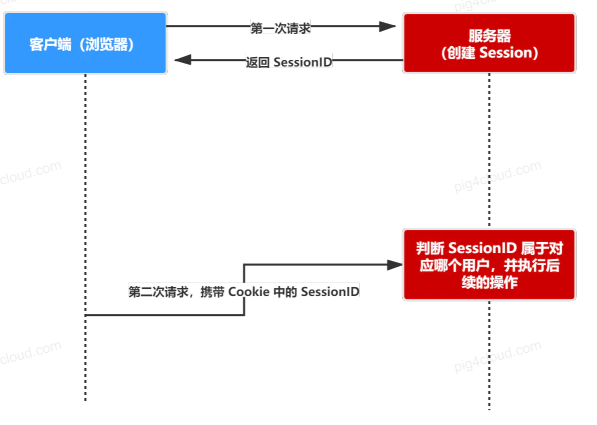
token, jwt, oauth2, session parsing
Machine Learning Overview
How do newcomers get started and learn software testing?
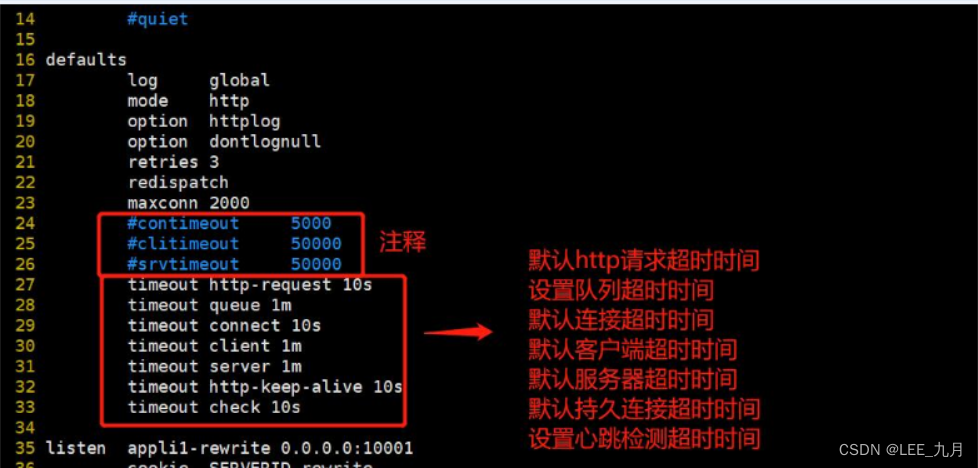
Haproxy搭建Web群集

浅析主流跨端技术方案

AUTOCAD——标注关联
A 35-year-old software testing engineer with a monthly salary of less than 2W, resigns and is afraid of not finding a job, what should he do?
![[BSidesCF 2019]Kookie](/img/29/19e7c244feb86b37ab32a53aa11f25.png)
[BSidesCF 2019]Kookie
随机推荐
Mysql's redo log detailed explanation
Analyses the mainstream across technology solutions
upload上传图片到腾讯云,如何上传图片
MySql index learning and use; (I think it is detailed enough)
Redis1: Introduction to Redis, basic features of Redis, relational database, non-relational database, database development stage
作业8.4 进程间的通信 管道与信号
how to measure distance from point to face in creo
UE4 后期处理体积 (角色受到伤害场景颜色变淡案例)
UE4 为子弹蓝图添加声音和粒子效果
[MRCTF2020] Ezpop (detailed)
大学物理---质点运动学
flink reads mongodb data source
C++ core programming
Day14 jenkins deployment
[BJDCTF2020]EasySearch
四位数显表头设计
What is the function of industrial-grade remote wireless transmission device?
【informix】解决启动报错大全,以及解决办法
【测量学】速成汇总——摘录高数帮
What is ASEMI photovoltaic diode, the role of photovoltaic diode