当前位置:网站首页>Minor spanning tree
Minor spanning tree
2022-07-05 04:37:00 【Bright autumn leaves】

. Let's find the minimum spanning tree first , Then enumerate the non tree edges in turn , Then add the edge to the tree , At the same time, remove an edge from the tree , So that the final picture is still a tree , Statistical minimum .
This method must be able to find non strict . Prove the following
Definition 1: set up T Figure G A spanning tree of , For non tree edges a And by the tree b, Insert edge a, And delete the edge b The operation of is recorded as (+a, -b). If T+a-b after , It's still a spanning tree , call (+a,-b) yes T A viable exchange for .
Definition 2: Called by T The new set of spanning trees obtained by a feasible transformation is called T Adjacent sets of .
Enumerating external edges in practice , Deleting an edge in a tree is enumeration MGT Adjacent sets of .
Theorem : The next smallest spanning tree must be in the neighborhood of the smallest spanning tree
Theorem proving :
Counter evidence , If there is a small spanning tree that is different from the minimum spanning tree k side , Sort do kruskal, Find the first side different from the second side , On the edge of the tree t Connect ab.
We will connect secondary schools ab One of the sides p Replace with t, Then small will become smaller ( Because of the order kruskal) For such a feasible exchange, we let the number of sides of the sub small spanning tree and the minimum spanning tree be different k-1. This operation can be continued until only 1 side . So the next smallest spanning tree must be in the adjacent set of the smallest spanning tree .
// New spanning tree newsum = sum - w( Inside the tree 2 spot The edge between ) + w( Outside the tree 2 The edge between points )
//(1) if newsum < sum ( be sum It must not be the minimum spanning tree edge weight sum contradiction )
// therefore sum > newsum ( Strictly sub small spanning trees )
//(2) if w( Outside the tree 2 The edge between points ) (a - b Two swords ) Not the biggest that Minimum spanning tree You can definitely get to this side
// contradiction
// therefore Be sure to get The largest side between two points Come on Replace new edge
// If new edge == The largest side between two points be Take the second largest
```
#include <bits/stdc++.h>
using namespace std;
#define io std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define x first
#define y second
#define fr front
#define db double
//int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
//int dx[8] = {-1, -1, -1, 0, 1, 1, 1, 0};
//int dy[8] = {-1, 0, 1, 1, 1, 0, -1, -1};
//int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
//int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
typedef pair<int, int> PII;
typedef long long LL ;
const int N = 10010, M = 510;
struct edge
{
int a, b, c, f;
bool operator< (edge x)
{
return c < x.c;
}
}g[N];
int n, m;
int h[M], e[N], w[N], ne[N], idx;// Store the minimum spanning tree
int dist1[M][M], dist2[M][M];// The farthest distance between two points in the tree And Second distance
int p[M];
void add(int a, int b, int c) // Add an edge a->b, The boundary right is c
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int find(int x) // Union checking set
{
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void dfs(int u, int f, int m1, int m2, int ds1[], int ds2[])
{
ds1[u] = m1, ds2[u] = m2;
for (int i = h[u]; ~i ;i = ne[i])
{
int t = e[i];
if (t != f)
{
int td1 = m1, td2 = m2;
if (w[i] > td1) td2 = td1, td1 = w[i];
else if (w[i] < td1 && w[i] > td2) td2 = w[i];
dfs(t, u, td1, td2, ds1, ds2);
}
}
}
int main()
{
io;
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 0;i < m;i ++ )
{
int a, b, c, f = 0;
cin >> a >> b >> c;
g[i] = {a, b, c, f};
}
for (int i = 1;i <= n;i ++ ) p[i] = i;
// Find the minimum spanning tree
sort(g, g + m);
LL sum = 0;
for (int i = 0;i < m;i ++ )
{
int a = g[i].a, b = g[i].b, c = g[i].c;
int x = find(a), y = find(b);
if (x != y)
{
add(a, b, c), add(b, a, c); // Store the second smallest spanning tree
g[i].f = 1; // Mark in the tree
p[x] = y;
sum += c;
}
}
// New spanning tree newsum = sum - w( Inside the tree 2 spot The edge between ) + w( Outside the tree 2 The edge between points )
//(1) if newsum < sum ( be sum It must not be the minimum spanning tree edge weight sum contradiction )
// therefore sum > newsum ( Strictly sub small spanning trees )
//(2) if w( Outside the tree 2 The edge between points ) (a - b Two swords ) Not the biggest that Minimum spanning tree You can definitely get to this side
// contradiction
// therefore Be sure to get The largest side between two points Come on Replace new edge
// If new edge == The largest side between two points be Take the second largest
// Find in the spanning tree The farthest distance between two points And Second distance
for (int i = 1;i <= n;i ++ ) dfs(i, -1, -1e9, -1e9, dist1[i], dist2[i]);
LL ans = 1e18;
for (int i = 0;i < m;i ++ )
if (!g[i].f) // Not only the edges in the minimum spanning tree
{
int a = g[i].a, b = g[i].b, c = g[i].c;
LL t;
if (c > dist1[a][b])
t = sum + c - dist1[a][b];
else if (c > dist2[a][b])
t = sum + c - dist2[a][b];
ans = min(ans, t);
}
cout << ans << endl;
return 0;
}
边栏推荐
- Here comes the Lantern Festival red envelope!
- Fonction (sujette aux erreurs)
- Discussion on the dimension of confrontation subspace
- How to remove installed elpa package
- [crampon game] MC tutorial - first day of survival
- TPG x AIDU | AI leading talent recruitment plan in progress!
- All in one 1413: determine base
- 程序员应该怎么学数学
- [moteur illusoire UE] il ne faut que six étapes pour réaliser le déploiement du flux de pixels ue5 et éviter les détours! (4.26 et 4.27 principes similaires)
- Convert Boolean to integer value PHP - Convert Boolean to integer value PHP
猜你喜欢

美国5G Open RAN再遭重大挫败,抗衡中国5G技术的图谋已告失败
How should programmers learn mathematics

CSDN正文自动生成目录

Raki's notes on reading paper: code and named entity recognition in stackoverflow
![[popular science] basic knowledge of thermal design: heat dissipation analysis of 5g optical devices](/img/45/380e739f5eed33626c363756f814d3.png)
[popular science] basic knowledge of thermal design: heat dissipation analysis of 5g optical devices
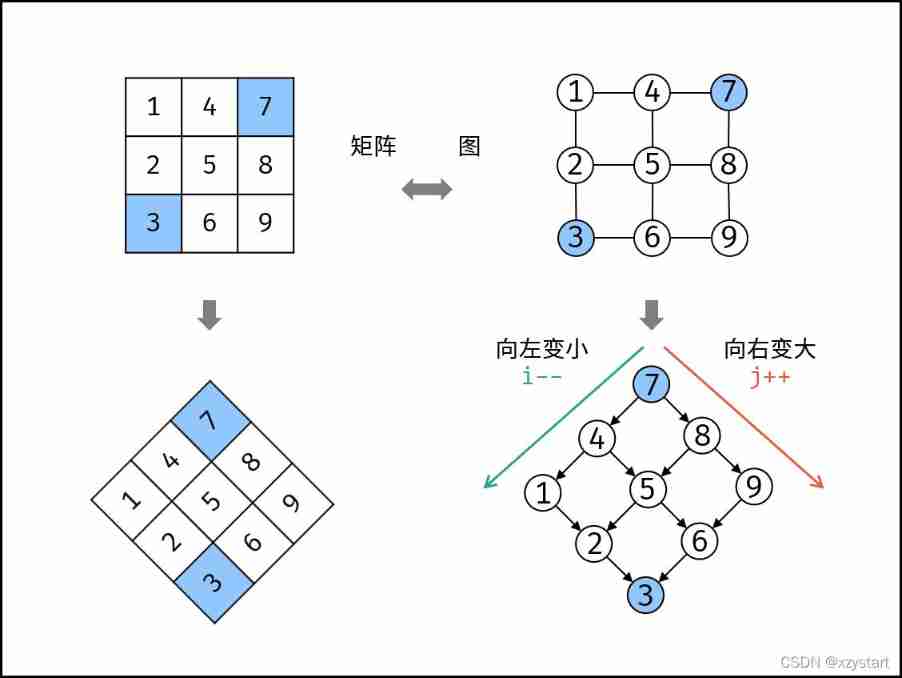
Sword finger offer 04 Search in two-dimensional array
【FineBI】使用FineBI制作自定义地图过程
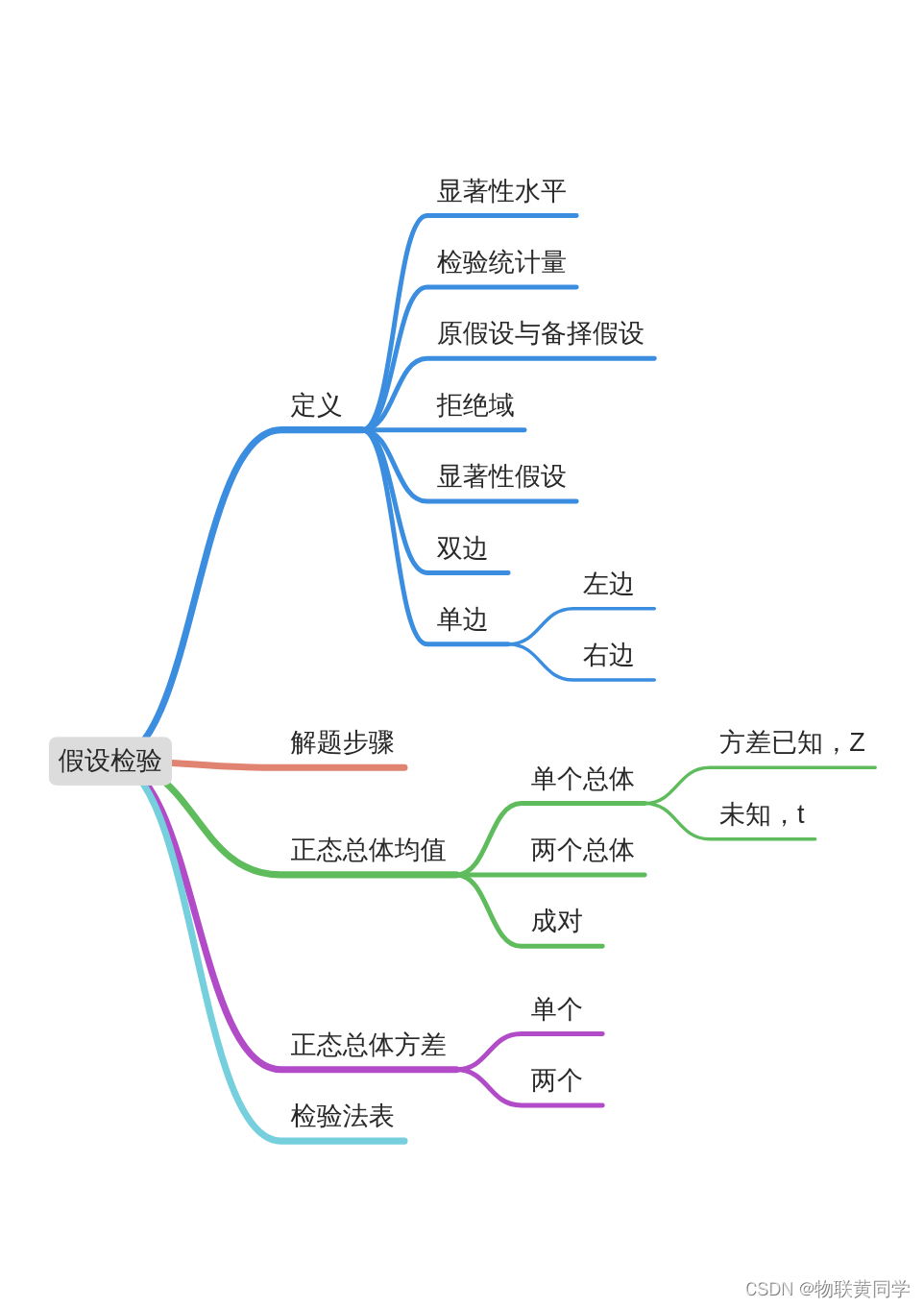
假设检验——《概率论与数理统计》第八章学习笔记
Is there a sudden failure on the line? How to make emergency diagnosis, troubleshooting and recovery
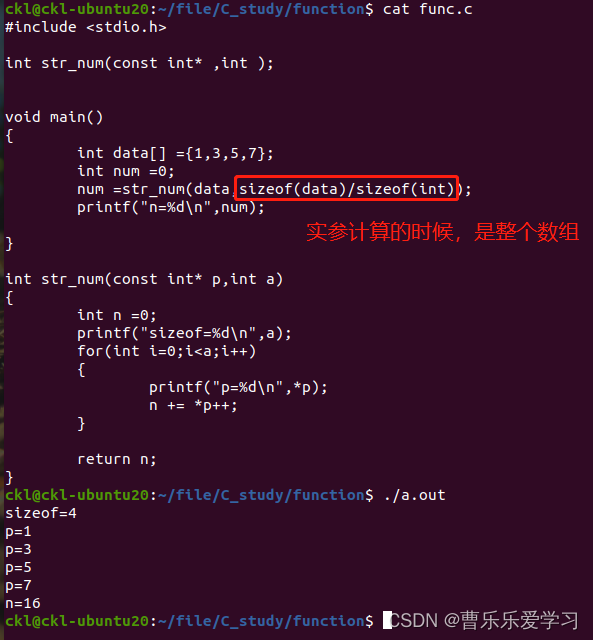
函数(易错)
随机推荐
C26451: arithmetic overflow: use the operator * on a 4-byte value, and then convert the result to an 8-byte value. To avoid overflow, cast the value to wide type before calling the operator * (io.2)
Solution of circular dependency
windows下Redis-cluster集群搭建
About the prompt loading after appscan is opened: guilogic, it keeps loading and gets stuck. My personal solution. (it may be the first solution available in the whole network at present)
Network security - record web vulnerability fixes
Qt蓝牙:搜索蓝牙设备的类——QBluetoothDeviceDiscoveryAgent
All in one 1413: determine base
Mxnet imports various libcudarts * so、 libcuda*. So not found
Live broadcast preview | container service ack elasticity prediction best practice
Function template
SQL set operation
PHP reads the INI file and writes the modified content
Sequelize. JS and hasmany - belongsto vs hasmany in serialize js
How to get the first few pieces of data of each group gracefully
Scope of package class package
Neural networks and deep learning Chapter 3: linear model reading questions
Ffmepg usage guide
防护电路中的元器件
介绍汉明距离及计算示例
Matplotlib draws three-dimensional scatter and surface graphs