当前位置:网站首页>Gaussian elimination acwing 884 Gauss elimination for solving XOR linear equations
Gaussian elimination acwing 884 Gauss elimination for solving XOR linear equations
2022-07-05 06:18:00 【T_ Y_ F666】
Gauss elimination AcWing 884. Gauss elimination is used to solve XOR linear equations
Original link
AcWing 884. Gauss elimination is used to solve XOR linear equations
Algorithm tags
Linear space Gauss elimination Exclusive or
Ideas

Code
#include<bits/stdc++.h>
#define int long long
#define abs fabs
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 105;
int a[N][N], eps = 1e-8;
int n;
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void put(int x) {
if(x<0) putchar('-'),x=-x;
if(x>=10) put(x/10);
putchar(x%10^48);
}
int gu(){// Gauss elimination , The answer lies in a[i][n] in ,0 <= i < n
// c Representative column r On behalf of the line
int c, r;
// Enumerate by column
for(c=0, r=0; c<n; ++c){
int t=r;
rep(i, r, n){
if(a[i][c]){// Find non-zero line
t=i;
break;
}
}
if(!a[t][c]){
continue;
}
rep(i, c, n+1){// Change non-zero lines to the top
swap(a[r][i], a[t][i]);
}
rep(i, r+1, n){// Use non-zero rows and the following columns to eliminate as 0
if(a[i][c]){
Rep(j, n, c){
a[i][j]^=a[r][j];
}
}
}
++r;
}
if(r<n){
rep(i, r, n){
if(abs(a[i][n])>eps){
return 2;// unsolvable
}
}
return 1;// There are infinite sets of solutions
}
Rep(i, n-1, 0){
rep(j, i+1, n){
a[i][n]^=a[i][j]*a[j][n];
}
}
return 0;// There is a unique solution
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
n=read();
rep(i, 0, n){
rep(j, 0, n+1){
a[i][j]=read();
}
}
int t=gu();
if(t==2){
puts("No solution");
}else if(t==1){
puts("Multiple sets of solutions");
}else{
rep(i, 0, n){
printf("%lld\n", a[i][n]);
}
}
return 0;
}
Originality is not easy.
Reprint please indicate the source
If it helps you Don't forget to praise and support 
边栏推荐
- Sqlmap tutorial (II) practical skills I
- [rust notes] 16 input and output (Part 1)
- [rust notes] 15 string and text (Part 1)
- SQLMAP使用教程(二)实战技巧一
- 4. 对象映射 - Mapping.Mapster
- Spark中groupByKey() 和 reduceByKey() 和combineByKey()
- leetcode-1200:最小绝对差
- Nested method, calculation attribute is not applicable, use methods
- Sqlmap tutorial (1)
- Is it impossible for lamda to wake up?
猜你喜欢
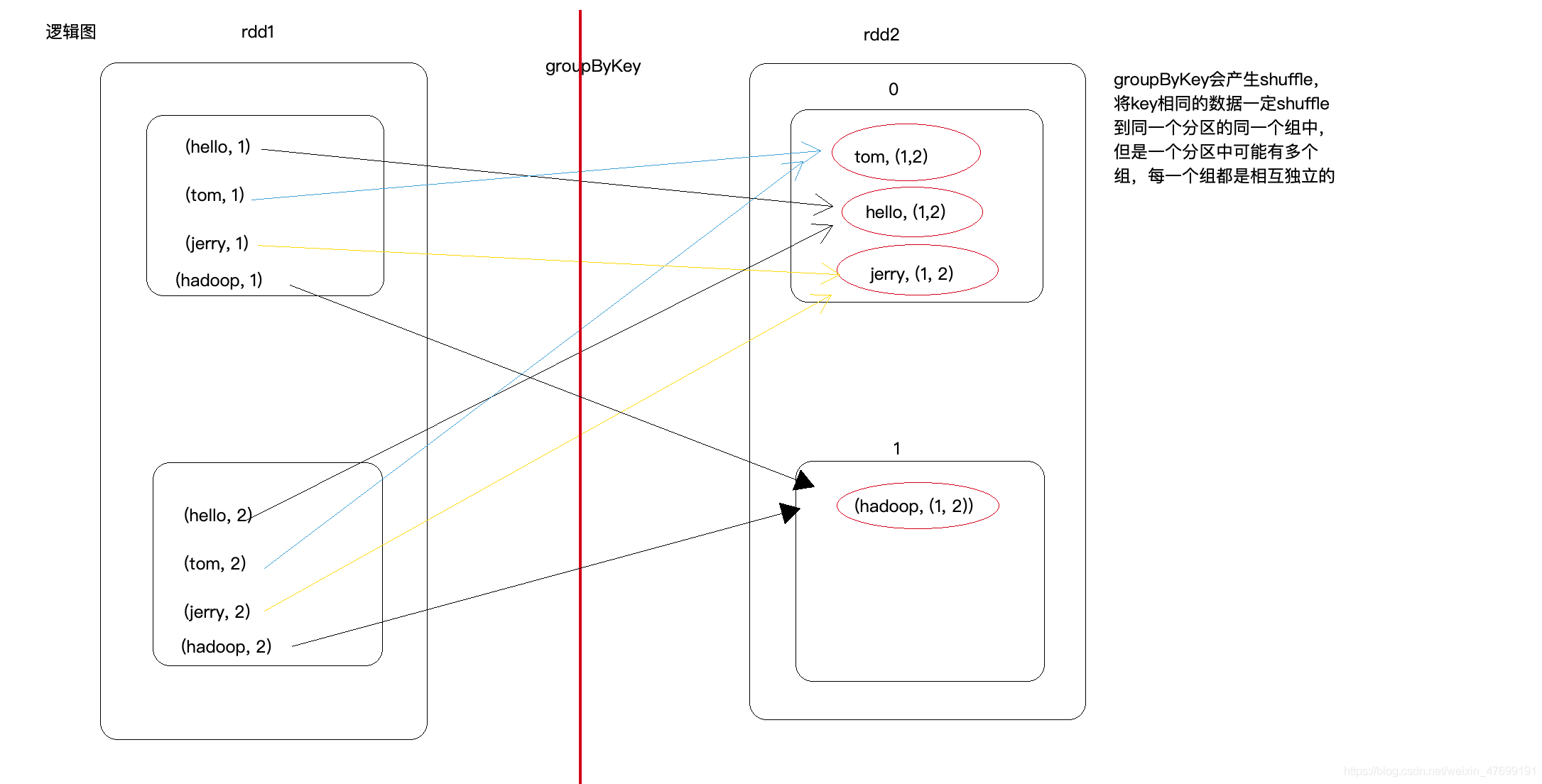
Groupbykey() and reducebykey() and combinebykey() in spark
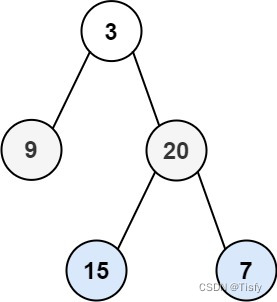
LeetCode 0107. Sequence traversal of binary tree II - another method
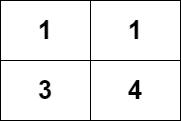
Leetcode-6110: number of incremental paths in the grid graph
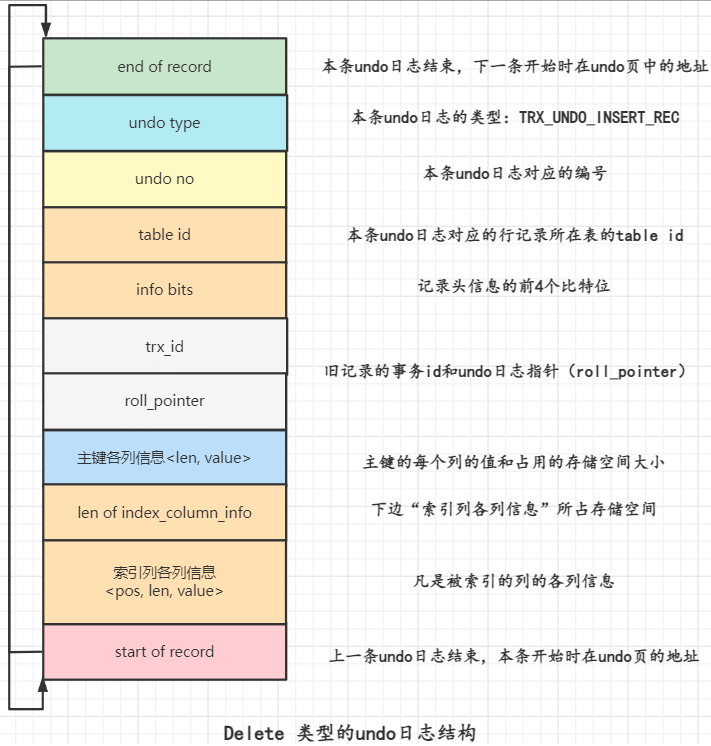
MySQL怎么运行的系列(八)14张图说明白MySQL事务原子性和undo日志原理

liunx启动redis
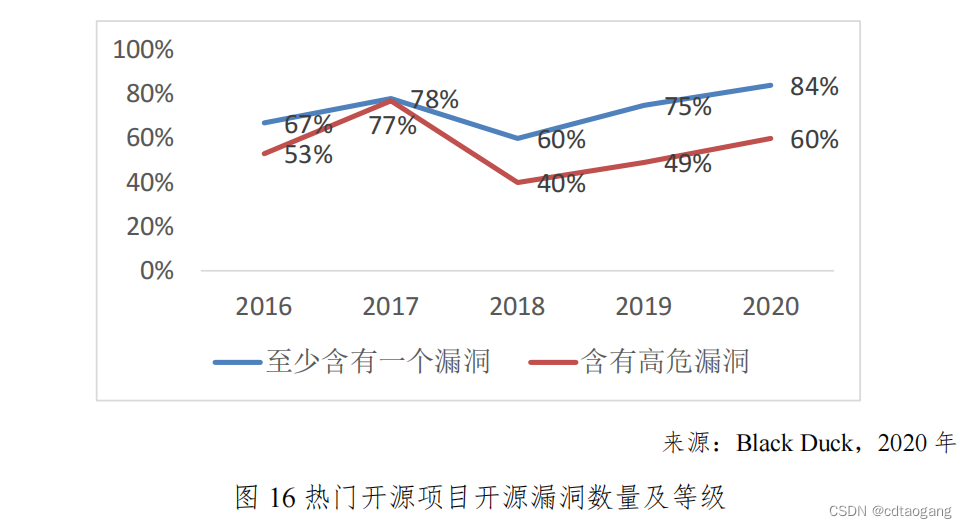
Open source storage is so popular, why do we insist on self-development?
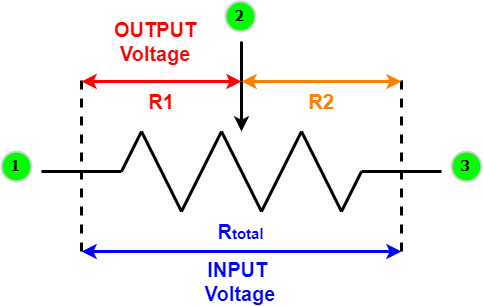
可变电阻器概述——结构、工作和不同应用

Appium基础 — 使用Appium的第一个Demo

Spark中groupByKey() 和 reduceByKey() 和combineByKey()
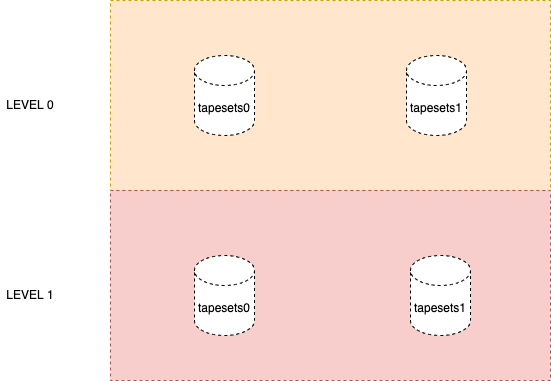
Matrixdb V4.5.0 was launched with a new mars2 storage engine!
随机推荐
[rust notes] 16 input and output (Part 1)
Basic explanation of typescript
QQ电脑版取消转义符输入表情
leetcode-6111:螺旋矩阵 IV
Leetcode-22: bracket generation
【LeetCode】Easy | 20. Valid parentheses
Doing SQL performance optimization is really eye-catching
MatrixDB v4.5.0 重磅发布,全新推出 MARS2 存储引擎!
MySQL advanced part 2: the use of indexes
The difference between CPU core and logical processor
C - XOR to all (binary topic)
Erreur de connexion Navicat à la base de données Oracle Ora - 28547 ou Ora - 03135
11-gorm-v2-02-create data
Sum of three terms (construction)
【Rust 笔记】17-并发(下)
leetcode-6109:知道秘密的人数
Leetcode-556: the next larger element III
对for(var i = 0;i < 5;i++) {setTimeout(() => console.log(i),1000)}的深入分析
1.13 - RISC/CISC
RGB LED infinite mirror controlled by Arduino