当前位置:网站首页>Shenji Bailian 3.53-kruskal
Shenji Bailian 3.53-kruskal
2022-07-02 05:58:00 【starnight531】
Kruskal
Food Guide :
Students who are familiar with the algorithm programming and stepping on the pit can directly jump to the code template to view the complete code Only the topic of basic algorithm will have the principle of the algorithm , Implementation steps , Code note , The code template , Explanation of code errors The problem of non basic algorithm focuses on problem analysis , Code implementation , And the necessary code misunderstanding
Title Description :
Given a n A little bit m Undirected graph of strip and edge , There may be double edges and self rings in the graph , The edge weight may be negative .
Find the sum of tree edge weights of the minimum spanning tree , If the minimum spanning tree does not exist, output impossible.
Given an undirected graph with weights G=(V,E), among V Represents the set of points in the graph ,E Represents a set of edges in a graph ,n=|V|,m=|E|.
from V All of n A vertex and E in n−1 An undirected connected subgraph composed of edges is called G A spanning tree of , The spanning tree in which the sum of the weights of the edges is the smallest is called an undirected graph G The minimum spanning tree of .Input format
The first line contains two integers n and m.
Next m That's ok , Each line contains three integers u,v,w, Indication point u Sum point v There is a weight of w The edge of .Output format
All in one line , If there is a minimum spanning tree , Then an integer is output , Represents the sum of tree edge weights of the minimum spanning tree , If the minimum spanning tree does not exist, output impossible.Data range
1≤n≤105,
1≤m≤2∗105,
The absolute values of the edge weights of the edges involved in the graph do not exceed 1000.sample input :
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
sample output :
6Title source :https://www.acwing.com/problem/content/861/
Topic analysis :
Number of edges m = 2*105, points n = 105, Sparse undirected graph
Self ring , Negative edge right , Heavy edge , Have no effect on the minimum spanning tree
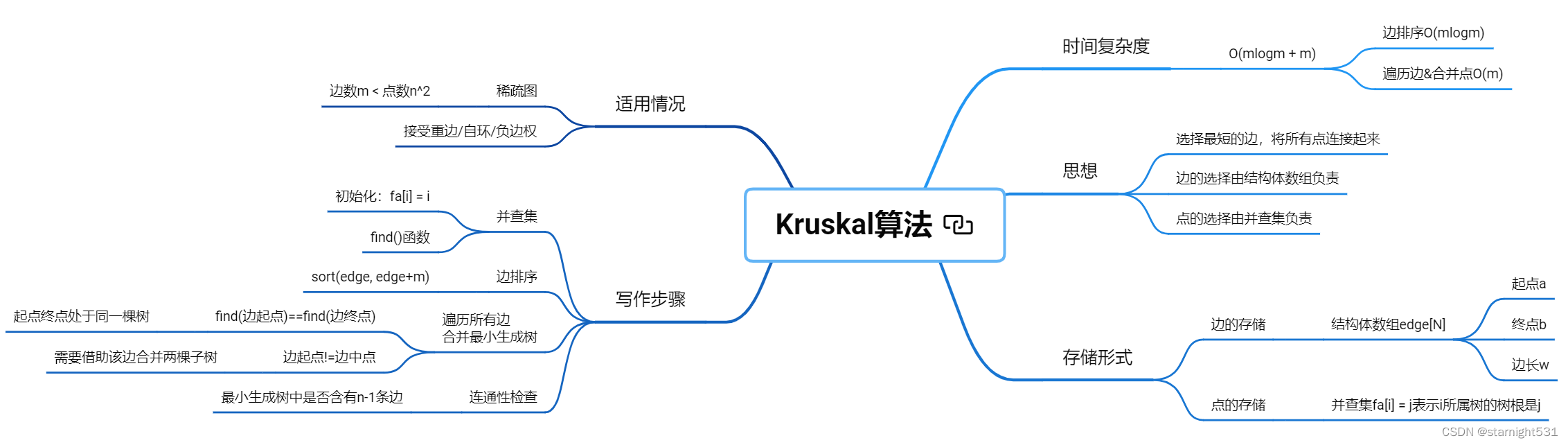
Specializing in the minimum spanning tree problem contains two algorithms : Starting from point Prim and Starting from the side Kruskal
Prim Algorithm time complexity O(n2), At worst, it takes time 1010, Far exceed 108
Kurskal Algorithm time complexity O(mlogm), At worst, it takes time 106
Next, let's talk about the implementation of the union search set , Starting from the edge in the figure kruskal Algorithm
Algorithm principle :
Template algorithm :
- Portal : Union checking set
- Portal :bellman-ford
- Portal : simple SPFA
Kruskal:
1. Application :
- Sparse graph , Number of edges m < points n2
- For heavy edges / Self ring / Negative edge right does not require
2. Storage form :
Edge storage :
Edges are stored as structural arrays , Easy to call sort() function
Each edge element contains three attributes : The starting point a, End b, Side length wStorage of minimum spanning tree :
Store the minimum spanning tree in the way of joint search
The final course n -1 The merger , take n-1 Points merged in a tree , All points fa[] It's all a point
If two points a b Of fa[] inequality , Then they are not on a minimum spanning tree , You need to connect the trees where they are located through the shortest edge
res Store the sum of the length of each side in the minimum spanning tree
cnt Record the number of edges contained in the minimum spanning tree , That is, how many sets have been merged
3. Algorithm is the core
Think from the result :
Finally, all points in the graph are connected into the minimum spanning tree
Each point enters the minimum spanning tree through edge connection
So as long as each point enters the minimum spanning tree , The length of the side with the help of is the shortest , The resulting tree is the minimum spanning tree
Three steps :
Sort all edges by weight from small to large O(mlogm):
Use STL Of sort() that will do , But edge classes need to be refactored operator <Enumerate each edge : The starting point a, End b, The weight w
If a b Not in the same set ( That is, on a tree , A non tree ), take ab Connect to the same set ( All non trees means all trees ).Compare cnt and n-1,cnt Less than n-1 Indicates that the minimum spanning tree connection is insufficient n A little bit , This graph is not a connected graph .
4. Simulation process
- The topic graph theory is as follows , Find the minimum spanning tree :

1. And search set initialization :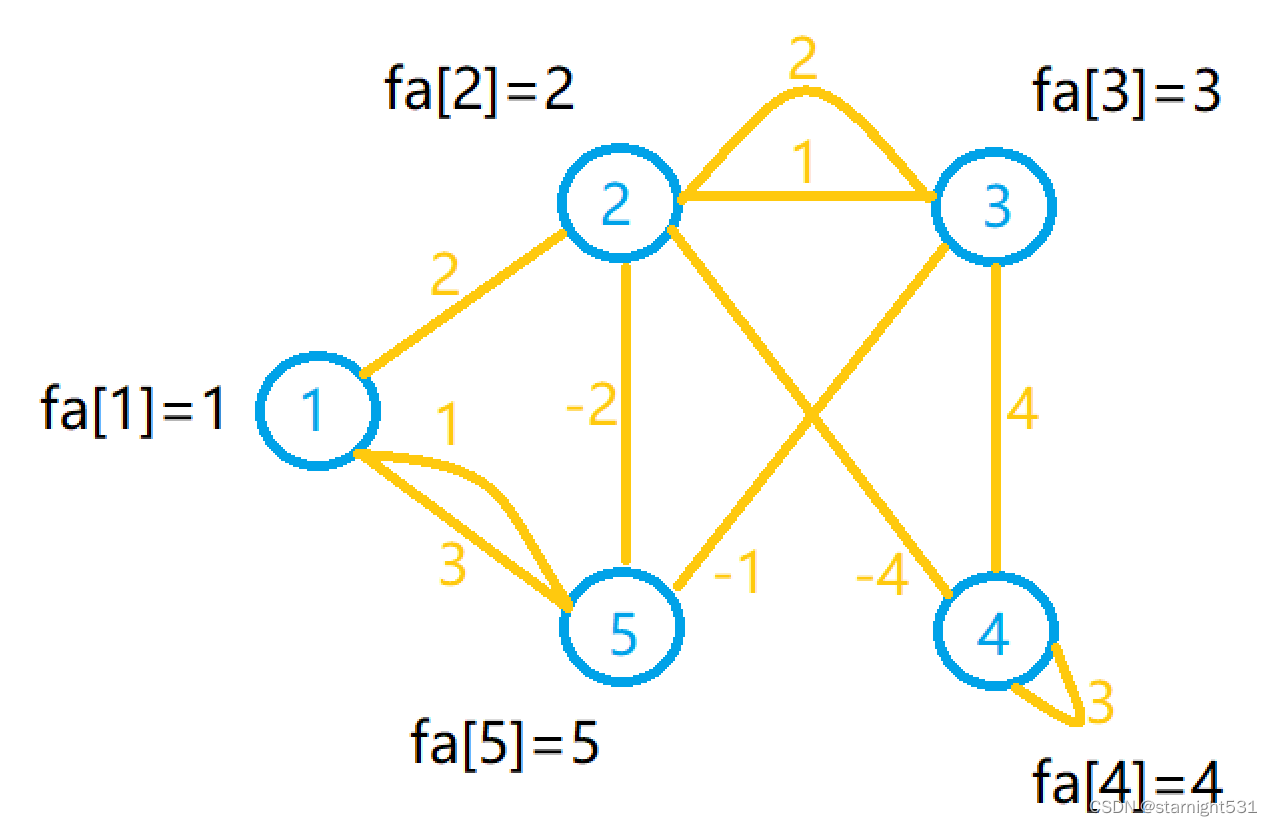
2. Side order :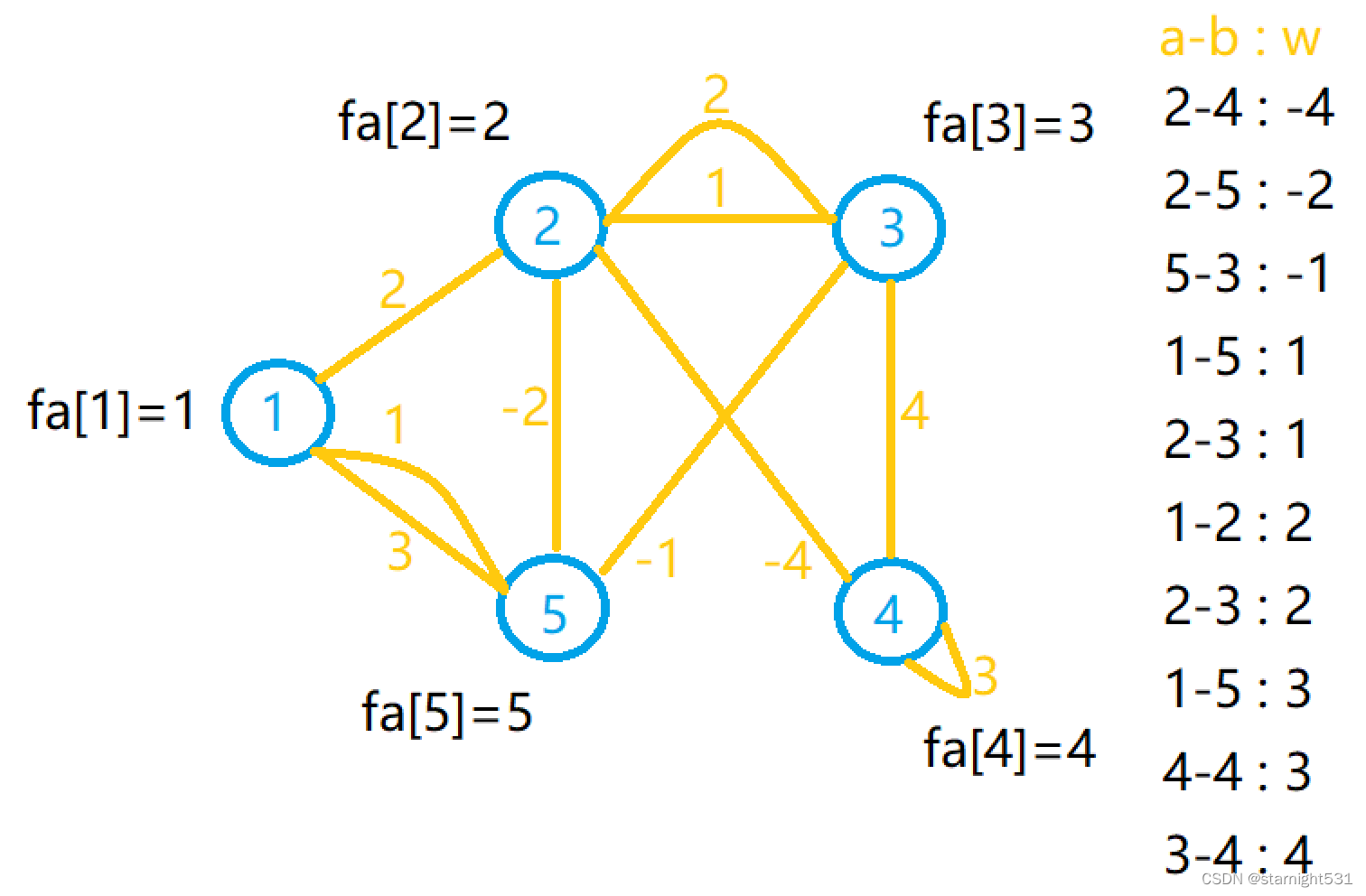
3. Ergodic edge + Subtree synthesis :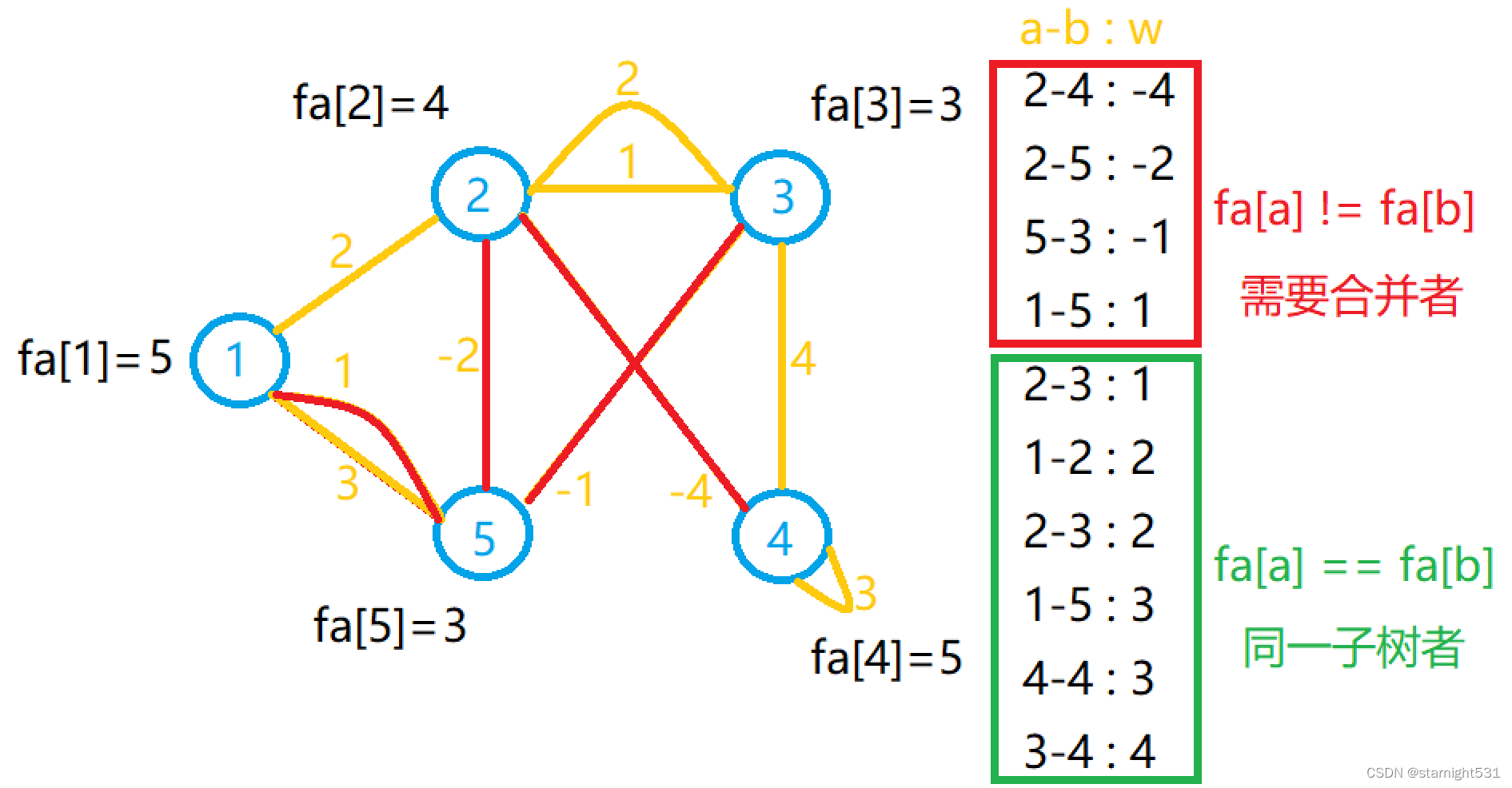
5. Time complexity analysis :
- sort() Side order :O(mlogm)
- Large loop traverses all edges :O(m)
- Inner merging : After recursively finding the root of the endpoint of the edge , All the following are O(1)
- Total time complexity :O(mlogm + m)
Writing steps :
1. Union checking set
- initialization : Each initial point is a tree ,fa[x] = x
- Find the root of the tree :find() Function recursively finds
- if find(a) != find(b) shows a b The trees of two points are not connected , You need the shortest edge to connect it
2. Side order
- Want to sort the edges , Need to reconstruct the structure < The operator
3. Ergodic edge
Traverse each edge from short to long ,
If the start and end of the edge are not connected , Then the edge is the shortest side length connecting two subtrees to become the minimum spanning tree
If the start and end of the edge are connected , Then both points are in the minimum spanning tree
4. Check connectivity
- If there is finally n-1 Secondary subtree merge , That is, there is n-1 side , Is the minimum spanning tree of all points in the whole graph
- If the final minimum spanning tree is insufficient n-1 side , Then the graph is unconnected , There is no minimum spanning tree of the whole graph
Code implementation :
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 200020;
struct Edge{
int a, b ,w;
bool operator<(const Edge &W) const{
return w < W.w;
}
}edge[M]; // It's easy to get wrong : The number of storage edges is used M
int n, m;
int fa[N];
void init(){
for(int i=1; i<=n; i++) fa[i] = i;
}
int find(int x){
if (x != fa[x])
fa[x] = find(fa[x]);
return fa[x];
}
int main(){
cin >>n >>m;
for(int i=0; i<m; i++){
cin >>edge[i].a >> edge[i].b >>edge[i].w;
}
sort(edge, edge+m);
init();
int cnt = 0, res = 0;
for(int i=0; i<m; i++){
int a = edge[i].a;
int b = edge[i].b;
a = find(a);
b = find(b);
if (a != b){
cnt++;
res += edge[i].w;
fa[a] = b;
}
}
if (cnt == n-1) cout<<res;
else cout<<"impossible"<<endl;
}
Code errors :
1. One sentence summary Kruskal
Choose the shortest edge first , Connect all points to the minimum spanning tree set
Structure array solves the problem of edges ,fa[] And look up the array to solve the problem of points
Start from the traversal edge , Connect all points into a minimum spanning tree
2. It's easy to get wrong : The size of the structure array is the maximum number of sides
const int N = 100010;
// Commonly used array size N Is the number of points
// The structure of this question is side , The size of the structure array should be the number of sides M
const int M = 100010;
struct Edge{
int a, b, w;
bool operator< (const Edge &W) const{
return w < W.w;
}
}edge[M];
// Because the number of sides is greater than the number of points , So continue to use N The length of several groups is easy to cross the content
3. Easy leakage point 1: And search set initialization
- Directly traverse the implementation fa[i] = i, It is the first step of using and querying sets , But it's easy to forget
- Encapsulated in the init() After the function , Find it easier to forget , What you forget is input nm Call after size init() function
4. Easy leakage point 2: Side order
- kruskal The core of is to preferentially select the short edge to connect all points
- Edge sorting is obviously the top priority , But because there is only one line sort(edge,edge+m), So easy to forget
5. Easy leakage point 3: Check connectivity
- The graph in the title is not necessarily a connected graph , Maybe the minimum spanning tree contains fewer than n-1, Points less than n
Thoughts on this article :
- This one feels dry again , about The shortest edge is preferred to connect all points The explanation of is not sufficient .
But you should understand this sentence by looking at the code - The shortest path and minimum spanning tree algorithm are explained , Graph theory only determines the maximum match between the remaining bipartite graph and the bipartite graph
The next chapter is the popular dynamic planning - Finish this blog post , Congratulations on having posted 《 Build a foundation - later stage 》

It's not far from entering fairyland , come on. 
边栏推荐
猜你喜欢
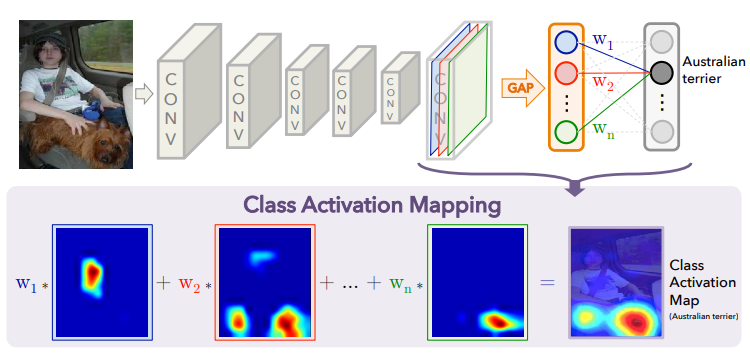
CNN可视化技术 -- CAM & Grad-CAM详解及pytorch简洁实现

测试 - 用例篇
![[paper translation] gcnet: non local networks meet squeeze exception networks and beyond](/img/7a/718162d08796f70251511101b3a61b.png)
[paper translation] gcnet: non local networks meet squeeze exception networks and beyond

Eco express micro engine system has supported one click deployment to cloud hosting

mysql的约束总结
![[PHP是否安装了 SOAP 扩]对于php实现soap代理的一个常见问题:Class ‘SoapClient‘ not found in PHP的处理方法](/img/25/73f11ab2711ed2cc9f20bc7f9116b6.png)
[PHP是否安装了 SOAP 扩]对于php实现soap代理的一个常见问题:Class ‘SoapClient‘ not found in PHP的处理方法
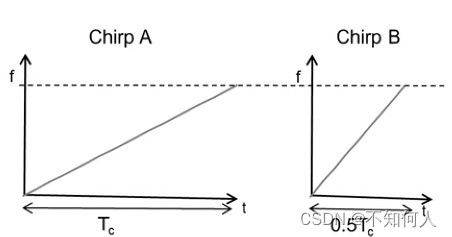
Ti millimeter wave radar learning (I)
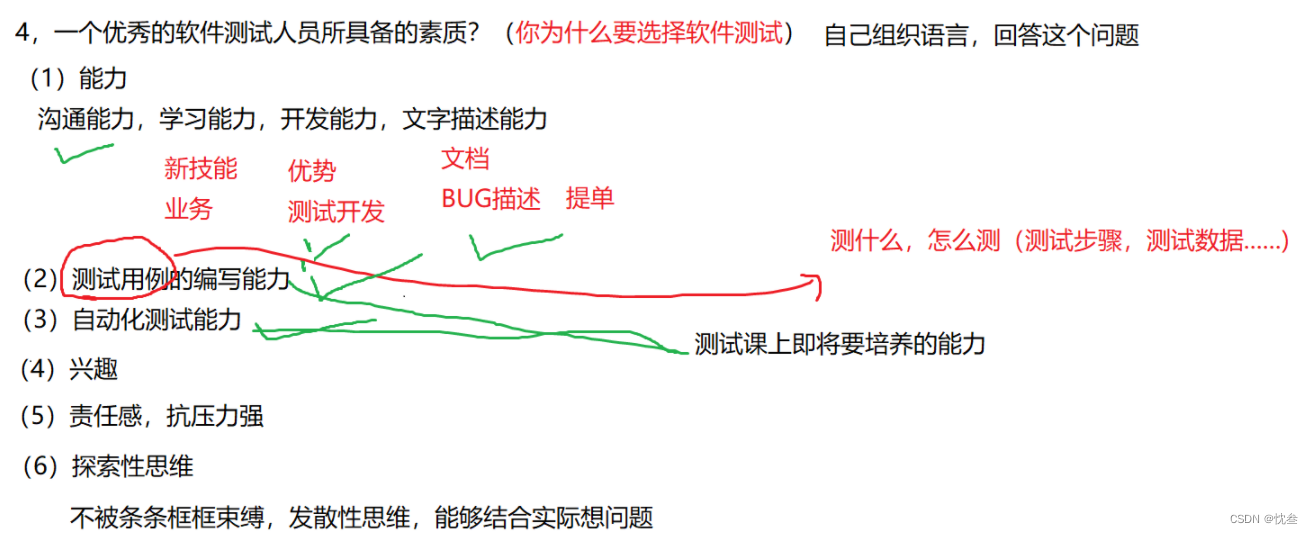
软件测试答疑篇

Brain and cognitive neuroscience matlab psychoolbox cognitive science experimental design - experimental design 4

脑与认知神经科学Matlab Psytoolbox认知科学实验设计——实验设计四
随机推荐
使用HBuilderX的一些常用功能
Verifying downloaded files using sha256 files
Conglin environmental protection rushes to the scientific and Technological Innovation Board: it plans to raise 2billion yuan, with an annual profit of more than 200million yuan
Go 学习笔记整合
Thunder on the ground! Another domestic 5g chip comes out: surpass Huawei and lead the world in performance?
File contains vulnerability (I)
PHP 开发与测试 Webservice(SOAP)-Win
Grbl software: basic knowledge of simple explanation
How to change the IP address of computer mobile phone simulator
Practice C language advanced address book design
Memcached installation
Common websites for Postgraduates in data mining
1035 Password
神机百炼3.53-Kruskal
Unity shader learning notes (3) URP rendering pipeline shaded PBR shader template (ASE optimized version)
cookie插件和localForage离线储存插件
正则表达式总结
TI毫米波雷达学习(一)
Lantern Festival gift - plant vs zombie game (realized by Matlab)
php读文件(读取文件内含有某字符串的指定行)