行列式学习笔记（一）

什么是行列式

教科书对二阶行列式的定义是这样的。
对于一个二元一次方程组：

\[\begin{cases} a_{11}x + a_{12}y = b_1\\ a_{21}x + a_{22}y = b_2 \end{cases} \]

经过消元可以得到：

\[(a_{12}a_{21}-a_{22}a_{11})y=a_{21}b_1-a_{11}b_2 \]

\(x\) 的解同理可得。
我们发现当 \(a_{12}a_{21} \neq a_{22}a_{11}\) 方程有唯一解。
这时我们这样来表示 \(a_{11}a_{22}-a_{12}a_{21}\)：

\[\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22}\\ \end{vmatrix} = a_{11}a_{22}-a_{12}a_{21}\]

所以我根本没有搞懂有什么用。

---

下面来介绍一种比较好懂的理解方法。
我们知道“ 矩阵可以表示一组向量，方阵表示 \(n\) 个 \(n\) 维向量 ”。
也就是每行看成一个向量，竖着把所有向量合并可以确定一个 \(n\) 维的图形。
来张二维的图看一看：

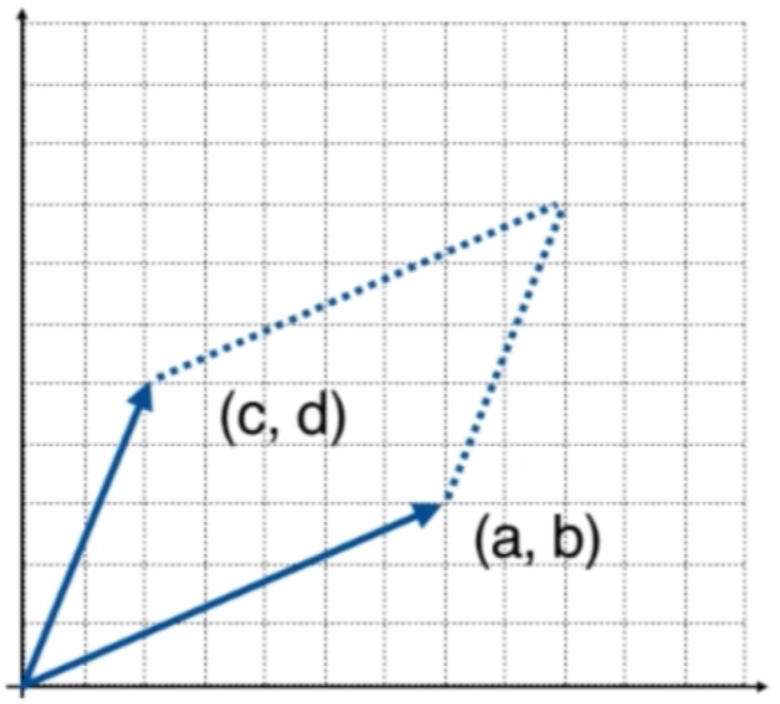
我们的二阶行列式在上图中就表示平行四边形的面积。
当然，二维是面积，三维是体积，四维是 ？？？ ……
上面这个平行四边形面积可以表示为：

\[\det A = \begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} \]

注意到，每一行都对应上图中的一个向量。

行列式的求法

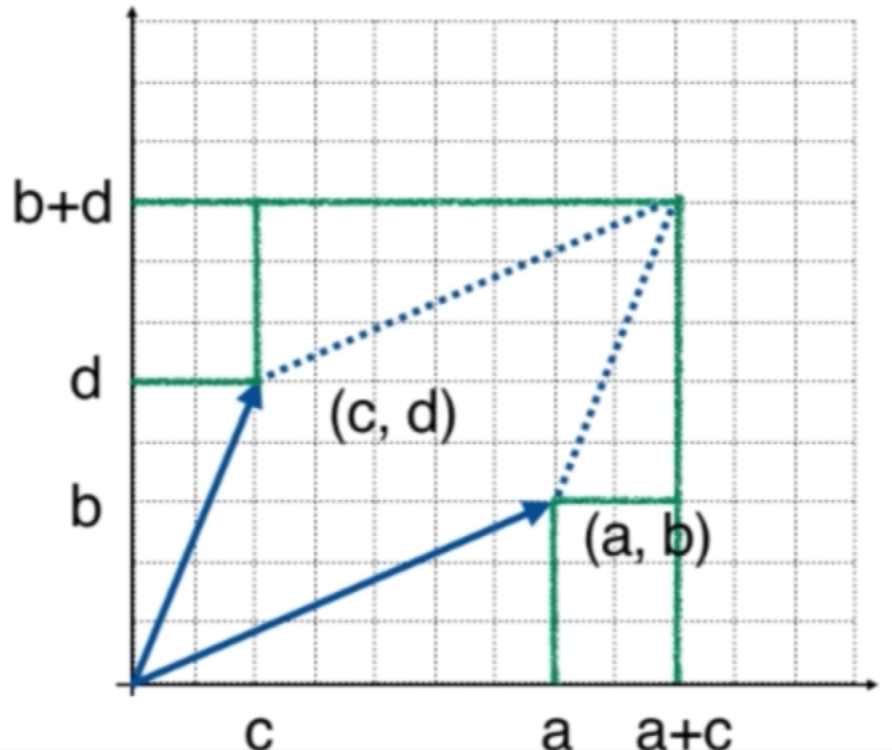
我们从小学数学入手，先求上述平行四边形的面积（辅助线做法省略）

\[\begin{split} S_{平行四边形} &=(a+c)(b+d)-2bc-cd-ab \\ &=ad-bc\\ &=\det A \end{split}\\ \]

也就是：

\[\begin {vmatrix} a &b \\ c &d \\ \end {vmatrix} = ad-bc \]

行列式的基本性质

下面以二阶行列式展开讨论。

性质一

\[\det I = 1 \]

\(I\) 表示单位矩阵，这很好理解：
所有向量都是 “横平竖直” 且长度都是一，面积一定是 \(1\)。

性质二

交换行列式的两行，则行列式的值取反。
用数学公式表示：

\[\begin{vmatrix} a & b\\ c & d\\ \end{vmatrix}= -\begin{vmatrix} c &d\\ a & b\\ \end{vmatrix} \]

证明很简单：

\[\begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} = ad-bc\\ \]

\[\begin{split} \begin{vmatrix} c &d\\ a & b\\ \end{vmatrix}&=bc-ad\\ &=-(ad-bc)\\ &=-\begin{vmatrix} c &d\\ a & b\\ \end{vmatrix} \end{split} \]

性质三

直接用数学公式表达吧。（语文不行）

\[\begin{vmatrix} ka & kb\\ c &d\\ \end{vmatrix} =k \begin{vmatrix} a & b\\ c &d\\ \end{vmatrix} \]

简单证明一下吧。

\[\begin{split} \begin{vmatrix} ka & kb\\ c &d\\ \end{vmatrix} &= kad-kbc\\&=k(ad-bc) \end{split} \]

注意：\(\det (kA) \neq k\det (A)\)
对于二阶行列式：

\[\begin{split} \det (kA) &= \begin {vmatrix} ka &kb\\ kc & kd\\ \end {vmatrix}\\ &=ka\times kd - kc \times kb\\ &=k^2(ad-bc)\\ &=k^2 \begin{vmatrix} a &b\\ c & d\\ \end {vmatrix}=k ^2\det (A) \end {split} \]

由此可以推出，对于 \(n\) 阶的行列式：

\[\det (kA)=k^n\det (A) \]

性质四

方阵的某一行加上一行数，则有：

\[\begin{vmatrix} a+a' & b + b'\\ c & d\\ \end{vmatrix} =\begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} + \begin{vmatrix} a' & b'\\ c & d\\ \end{vmatrix} \]

证明一下：

\[\begin{split} \begin{vmatrix} a+a' & b + b'\\ c & d\\ \end{vmatrix} &=(a+a')d-c(b+b')\\ &=ad+a'd-cb-cb'\\ &=(ad-bc)+(a'd-b'c)\\ &= \begin{vmatrix} a & b\\ c & d\\ \end{vmatrix} + \begin{vmatrix} a' & b'\\ c & d\\ \end{vmatrix} \end{split} \]