698. Divided into k equal subsets ●●

698. Divided into k Equal subsets ●●

describe

Given an array of integers nums And a positive integer k, find whether Divide this array into k A non empty subset , Its The sum is equal .

Example

Input ： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
Output ： True
explain ： It is possible to divide it into 4 A subset of （5）,（1,4）,（2,3）,（2,3） Equal to the sum .

Answer key

Reference link

First, the problem is abstracted ： Yes n A ball ,k A barrel , How to allocate the balls into the bucket so that the sum of the balls in each bucket is target. As shown in the figure below ：

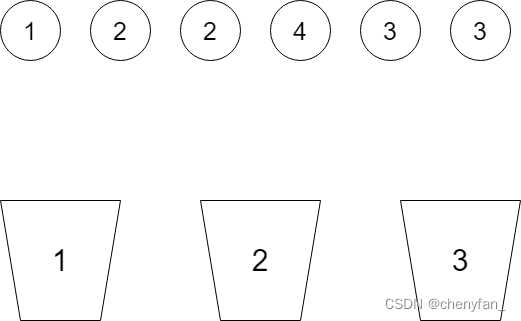
1. to flash back , The ball （ Numbers ） visual angle

From the perspective of the ball , Each ball needs to make three choices , namely ： Choose to put 1 Bucket number 、2 Bucket number 、3 Bucket number . All the balls need do $k^n$ Secondary selection .

Because backtracking is an idea of violent solution , So there are three choices for each ball , Only after the selection is performed can we know whether the selection is the optimal solution . To put it bluntly, it is to implement these three options in turn , If the selection is found to be non optimal after recursion to the following , Then start backtracking , Make other choices , Until all choices are traversed .

Pruning operations are critical .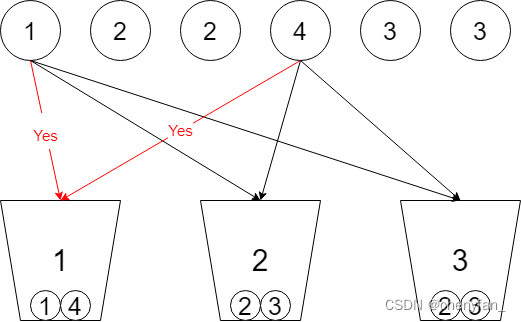

class Solution {
    
public:
    bool backtrack(int idx, vector<int>& nums, vector<int>& buckets, int target, int k){
    
        if(idx == nums.size()) return true;                     //  The end condition ： All elements are divided into buckets , At this time, the sum of each set must be equal 
        for(int i = 0; i < k; ++i){
    
            if (i > 0 && idx == 0) break ;                      //  The first element is the same in which bucket , So it fails to trace back to the first element （ prune ）
            if(buckets[i] + nums[idx] > target) continue;       //  prune , The sum of sets cannot be greater than target
            if(i > 0 && buckets[i] == buckets[i-1]) continue;   //  prune , The selection of the same set and can be seen as a repetition 
            buckets[i] += nums[idx];                            //  Join the collection i
            if(backtrack(idx+1, nums, buckets, target, k)) return true; //  recursive 
            buckets[i] -= nums[idx];                            //  to flash back 
        }
        return false;                                           // k  None of the barrels meet the requirements 
    }   

    bool canPartitionKSubsets(vector<int>& nums, int k) {
    
        int sum = 0, maxNum = 0;
        for(int num : nums){
    
            sum += num;
            if(maxNum < num) maxNum = num;
        }
        if(maxNum*k > sum || sum % k != 0) return false;    //  prune 
        int target = sum / k;                               //  Target set and 
        vector<int> buckets(k, 0);                          //  Bucket collection 
        sort(nums.begin(), nums.end(), greater<int>());     //  Descending , Fill in from big to small , Reduce the consumption of backtracking 
        return backtrack(0, nums, buckets, target, k);
    }
};

2. to flash back , bucket （ aggregate ） visual angle

From the perspective of the bucket , Each bucket requires six choices , namely ： Whether to choose 1 Put the ball in 、 Whether to choose 2 Put the ball in 、…、 Whether to choose 6 Put the ball in . All barrels need do $k{2}^n$ Secondary selection .

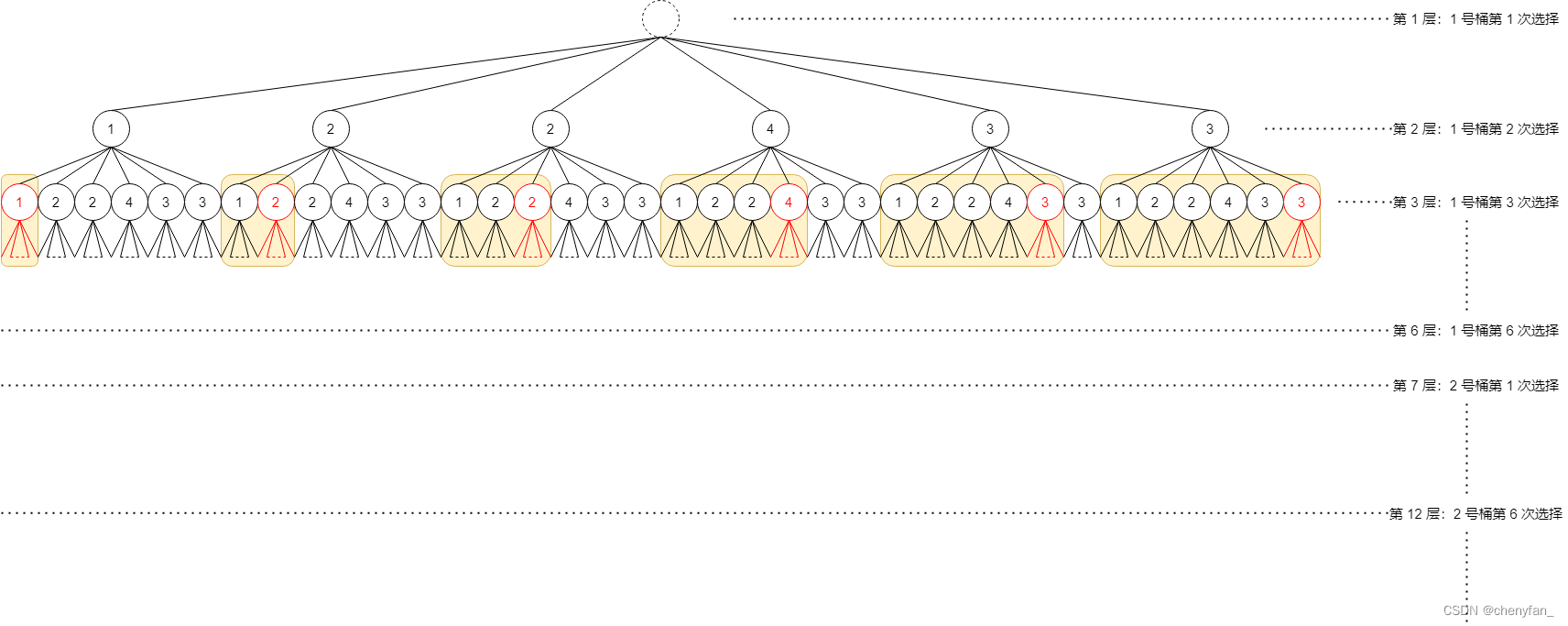
The following is 「 Bucket Perspective 」 Decision tree under

First, explain the decision tree , The first i Layer for j No. barrel makes No x Secondary selection , Choices to make ： Whether to choose 1 ～ 6 Ball No , until k End after all barrels are full ;

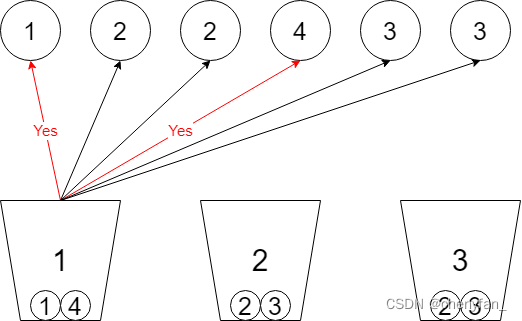
because , Each ball can only be selected by one bucket , So when a ball is selected by a bucket , The other bucket cannot choose the ball , See the branch marked in red in the following figure ;

The condition for judging whether a ball can be selected is ：(1) Whether the ball has been selected ？ (2) After putting the ball , Whether the bucket overflows ？

When the array is ordered , The choice of excluding the next case with the same value as the current one is crucial to reduce the time complexity .

class Solution {
    
public:
    unordered_set<vector<bool>> hash;
    bool backtrack(int start, vector<int>& nums, vector<bool>& used, vector<int>& buckets, int target, int k){
    
        if(k == 0) return true;                                 //  The end condition ： All barrels are full of elements 
        if(buckets[k-1] == target) return backtrack(0, nums, used, buckets, target, k-1);   //  The current barrel is full , Start loading the next bucket 
        for(int i = start; i < nums.size(); ++i){
                   //  Traverse each ball , Choose whether to load 
            if(used[i] == true) continue;                       //  The ball has been used 
            if(buckets[k-1] + nums[i] > target) continue;       //  prune , The sum of sets cannot be greater than target
            used[i] = true;                                     //  Select the ball and add it to the bucket 
            buckets[k-1] += nums[i];                            
            if(backtrack(i+1, nums, used, buckets, target, k)) return true; //  recursive , Start with the next ball 
            buckets[k-1] -= nums[i];                            //  to flash back 
            used[i] = false;        
            while (i + 1 < nums.size() && nums[i + 1] == nums[i]) ++i;      //  prune , In order , If the next one is the same as the current one, it will definitely not work 
        }
        return false;                                           //  All the balls cannot meet the conditions 
    }   

    bool canPartitionKSubsets(vector<int>& nums, int k) {
    
        int sum = 0, maxNum = 0;
        for(int num : nums){
    
            sum += num;
            if(maxNum < num) maxNum = num;
        }
        if(maxNum*k > sum || sum % k != 0) return false;    //  prune 
        int target = sum / k;                               //  Target set and 
        vector<int> buckets(k, 0);                          //  Bucket collection 
        vector<bool> used(nums.size(), false);              //  Use the tag 
        sort(nums.begin(), nums.end());                     //  Sort 
        return backtrack(0, nums, used, buckets, target, k);
    }
};

• The maximum array size is 16 individual , therefore bool The form of array tags can be optimized by using bit operation tags

int used = 0; initialization
(used >> i) & 1 == 1 Judgment No. i Whether the number has been used
used |= 1 << i; Mark the i Number
used ^= 1 << i; The first i Number unmarked