当前位置:网站首页>698. Divided into k equal subsets ●●
698. Divided into k equal subsets ●●
2022-07-05 23:24:00 【chenyfan_】
698. Divided into k Equal subsets ●●
describe
Given an array of integers nums And a positive integer k, find whether Divide this array into k A non empty subset , Its The sum is equal .
Example
Input : nums = [4, 3, 2, 3, 5, 2, 1], k = 4
Output : True
explain : It is possible to divide it into 4 A subset of (5),(1,4),(2,3),(2,3) Equal to the sum .
Answer key
First, the problem is abstracted : Yes n A ball ,k A barrel , How to allocate the balls into the bucket so that the sum of the balls in each bucket is target. As shown in the figure below :
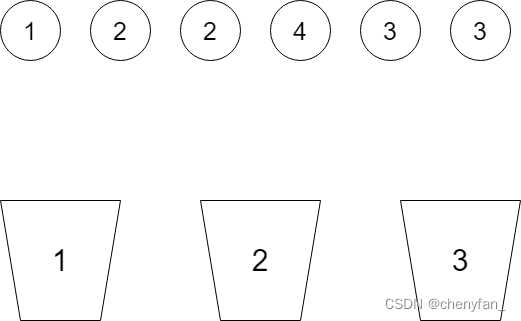
1. to flash back , The ball ( Numbers ) visual angle
From the perspective of the ball , Each ball needs to make three choices , namely : Choose to put 1 Bucket number 、2 Bucket number 、3 Bucket number . All the balls need do k n k^n kn Secondary selection .
Because backtracking is an idea of violent solution , So there are three choices for each ball , Only after the selection is performed can we know whether the selection is the optimal solution . To put it bluntly, it is to implement these three options in turn , If the selection is found to be non optimal after recursion to the following , Then start backtracking , Make other choices , Until all choices are traversed .
Pruning operations are critical .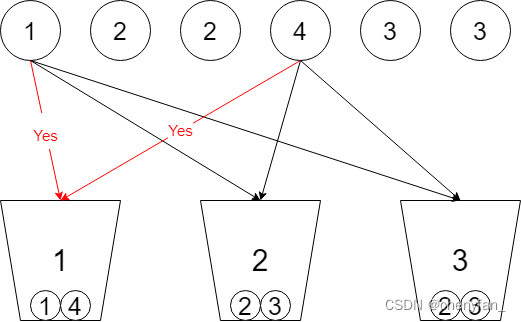
class Solution {
public:
bool backtrack(int idx, vector<int>& nums, vector<int>& buckets, int target, int k){
if(idx == nums.size()) return true; // The end condition : All elements are divided into buckets , At this time, the sum of each set must be equal
for(int i = 0; i < k; ++i){
if (i > 0 && idx == 0) break ; // The first element is the same in which bucket , So it fails to trace back to the first element ( prune )
if(buckets[i] + nums[idx] > target) continue; // prune , The sum of sets cannot be greater than target
if(i > 0 && buckets[i] == buckets[i-1]) continue; // prune , The selection of the same set and can be seen as a repetition
buckets[i] += nums[idx]; // Join the collection i
if(backtrack(idx+1, nums, buckets, target, k)) return true; // recursive
buckets[i] -= nums[idx]; // to flash back
}
return false; // k None of the barrels meet the requirements
}
bool canPartitionKSubsets(vector<int>& nums, int k) {
int sum = 0, maxNum = 0;
for(int num : nums){
sum += num;
if(maxNum < num) maxNum = num;
}
if(maxNum*k > sum || sum % k != 0) return false; // prune
int target = sum / k; // Target set and
vector<int> buckets(k, 0); // Bucket collection
sort(nums.begin(), nums.end(), greater<int>()); // Descending , Fill in from big to small , Reduce the consumption of backtracking
return backtrack(0, nums, buckets, target, k);
}
};
2. to flash back , bucket ( aggregate ) visual angle
From the perspective of the bucket , Each bucket requires six choices , namely : Whether to choose 1 Put the ball in 、 Whether to choose 2 Put the ball in 、…、 Whether to choose 6 Put the ball in . All barrels need do k 2 n k2^n k2n Secondary selection .
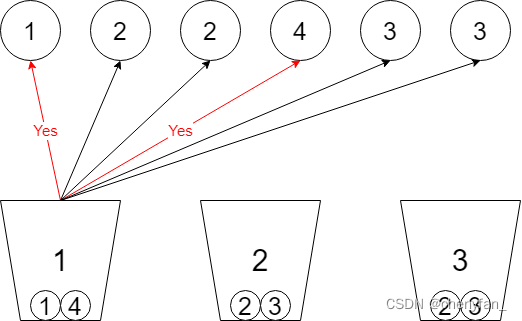
The following is 「 Bucket Perspective 」 Decision tree under
First, explain the decision tree , The first i Layer for j No. barrel makes No x Secondary selection , Choices to make : Whether to choose 1 ~ 6 Ball No , until k End after all barrels are full ;
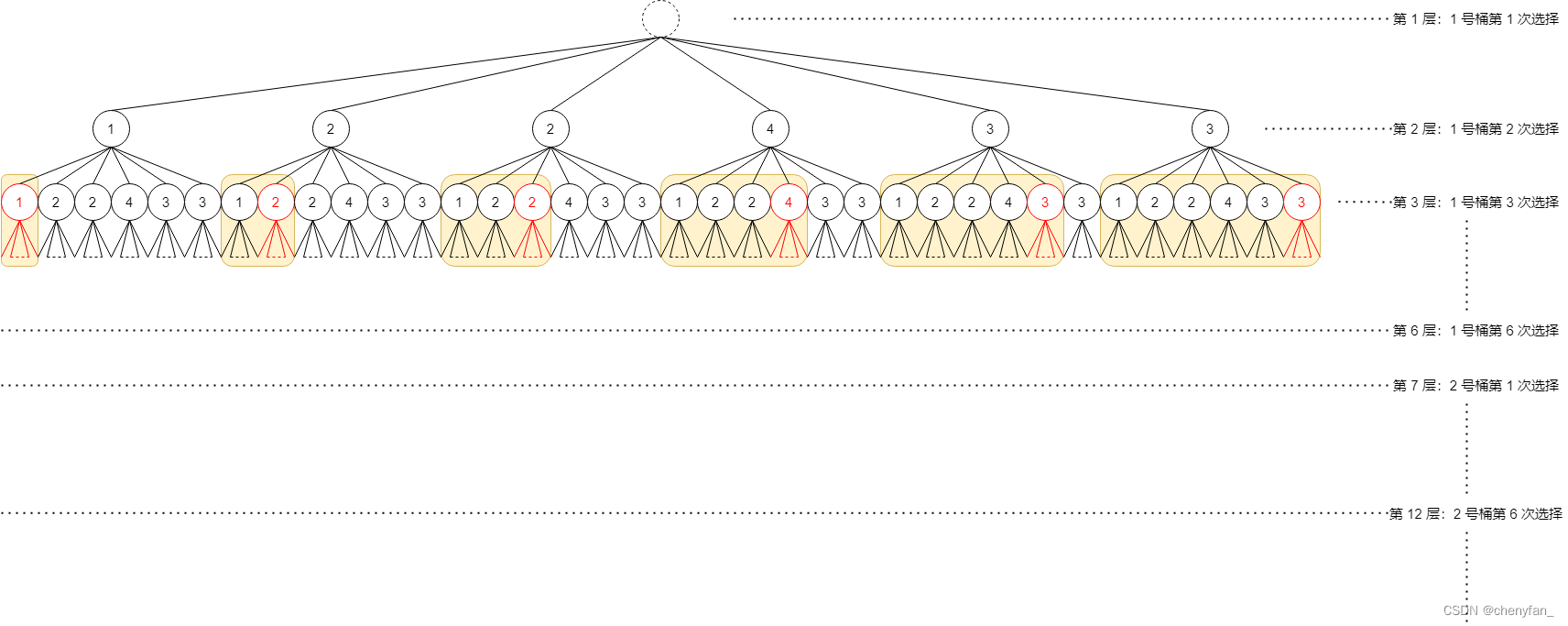
because , Each ball can only be selected by one bucket , So when a ball is selected by a bucket , The other bucket cannot choose the ball , See the branch marked in red in the following figure ;
The condition for judging whether a ball can be selected is :(1) Whether the ball has been selected ? (2) After putting the ball , Whether the bucket overflows ?
When the array is ordered , The choice of excluding the next case with the same value as the current one is crucial to reduce the time complexity .
class Solution {
public:
unordered_set<vector<bool>> hash;
bool backtrack(int start, vector<int>& nums, vector<bool>& used, vector<int>& buckets, int target, int k){
if(k == 0) return true; // The end condition : All barrels are full of elements
if(buckets[k-1] == target) return backtrack(0, nums, used, buckets, target, k-1); // The current barrel is full , Start loading the next bucket
for(int i = start; i < nums.size(); ++i){
// Traverse each ball , Choose whether to load
if(used[i] == true) continue; // The ball has been used
if(buckets[k-1] + nums[i] > target) continue; // prune , The sum of sets cannot be greater than target
used[i] = true; // Select the ball and add it to the bucket
buckets[k-1] += nums[i];
if(backtrack(i+1, nums, used, buckets, target, k)) return true; // recursive , Start with the next ball
buckets[k-1] -= nums[i]; // to flash back
used[i] = false;
while (i + 1 < nums.size() && nums[i + 1] == nums[i]) ++i; // prune , In order , If the next one is the same as the current one, it will definitely not work
}
return false; // All the balls cannot meet the conditions
}
bool canPartitionKSubsets(vector<int>& nums, int k) {
int sum = 0, maxNum = 0;
for(int num : nums){
sum += num;
if(maxNum < num) maxNum = num;
}
if(maxNum*k > sum || sum % k != 0) return false; // prune
int target = sum / k; // Target set and
vector<int> buckets(k, 0); // Bucket collection
vector<bool> used(nums.size(), false); // Use the tag
sort(nums.begin(), nums.end()); // Sort
return backtrack(0, nums, used, buckets, target, k);
}
};
- The maximum array size is 16 individual , therefore bool The form of array tags can be optimized by using bit operation tags
int used = 0; initialization (used >> i) & 1 == 1 Judgment No. i Whether the number has been used used |= 1 << i; Mark the i Number used ^= 1 << i; The first i Number unmarked
边栏推荐
- Multi view 3D reconstruction
- (4) UART application design and simulation verification 2 - RX module design (stateless machine)
- 两数之和、三数之和(排序+双指针)
- 2:第一章:认识JVM规范1:JVM简介;
- Go语言实现原理——锁实现原理
- 11gR2 Database Services for &quot;Policy&quot; and &quot;Administrator&quot; Managed Databases (文件 I
- idea 连接mysql ,直接贴配置文件的url 比较方便
- February 13, 2022 -5- maximum depth of binary tree
- Go language implementation principle -- map implementation principle
- Object detection based on impulse neural network
猜你喜欢
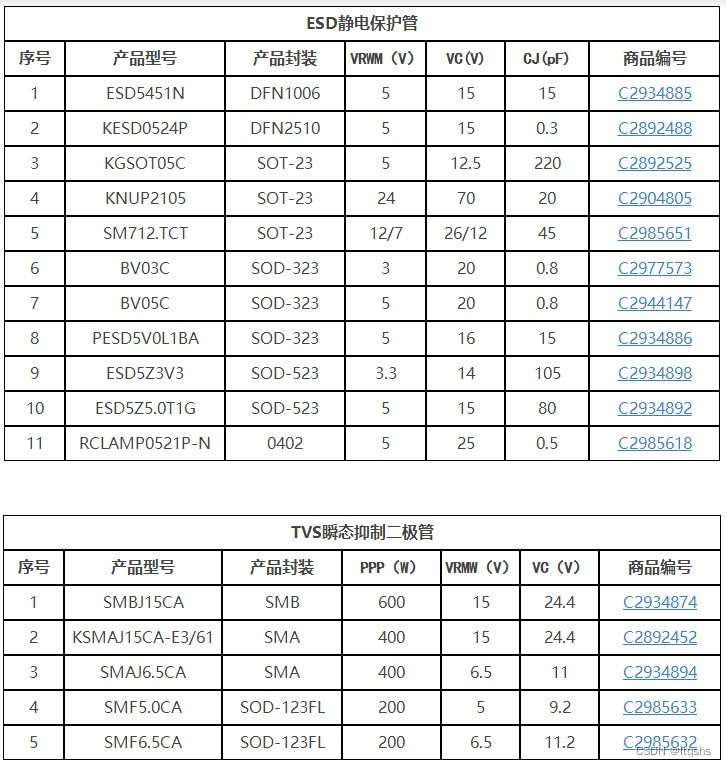
TVS管和ESD管的技术指标和选型指南-嘉立创推荐
Creative mode 1 - single case mode

LeetCode102. Sequence traversal of binary tree (output by layer and unified output)

Alibaba Tianchi SQL training camp task4 learning notes

3:第一章:认识JVM规范2:JVM规范,简介;
并查集实践
2022 registration examination for safety management personnel of hazardous chemical business units and simulated reexamination examination for safety management personnel of hazardous chemical busines

开关电源Buck电路CCM及DCM工作模式
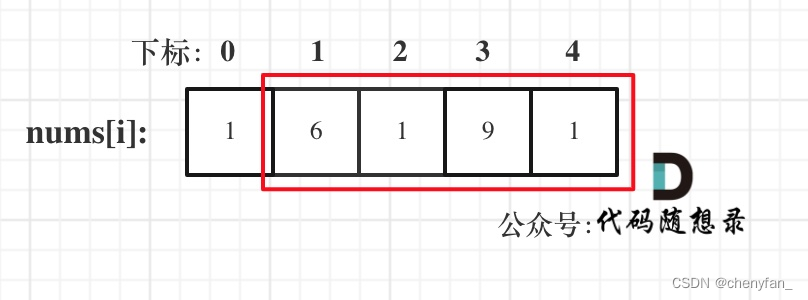
动态规划 之 打家劫舍
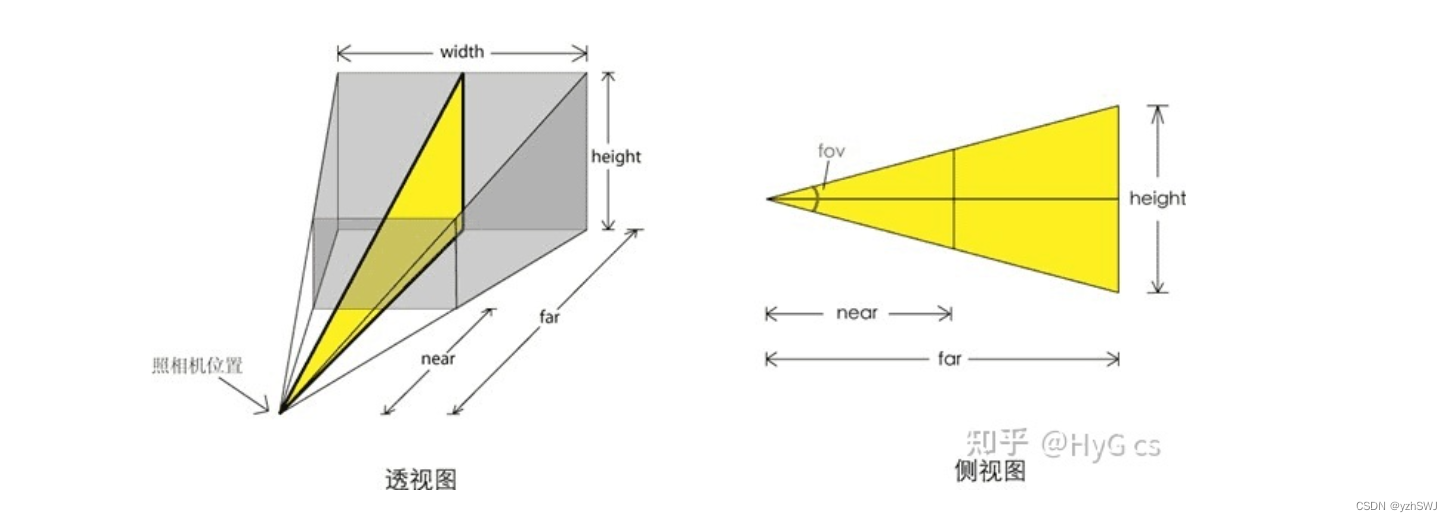
Three.js-01 入门
随机推荐
芯源&立创EDA训练营——无刷电机驱动
Registration and skills of hoisting machinery command examination in 2022
Déterminer si un arbre binaire est un arbre binaire complet
Judge whether the binary tree is a complete binary tree
Mathematical formula screenshot recognition artifact mathpix unlimited use tutorial
LeetCode——Add Binary
3D reconstruction of point cloud
Data type, variable declaration, global variable and i/o mapping of PLC programming basis (CoDeSys)
Fix the memory structure of JVM in one article
What is the process of building a website
asp.net弹出层实例
LeetCode——Add Binary
poj 2762 Going from u to v or from v to u? (推断它是否是一个薄弱环节图)
Sum of two numbers, sum of three numbers (sort + double pointer)
February 13, 2022-4-symmetric binary tree
February 13, 2022 -5- maximum depth of binary tree
MySQL (2) -- simple query, conditional query
Southeast Asia e-commerce guide, how do sellers layout the Southeast Asia market?
Krypton Factor purple book chapter 7 violent solution
698. 划分为k个相等的子集 ●●