当前位置:网站首页>Recursion and divide and conquer strategy
Recursion and divide and conquer strategy
2022-07-04 10:25:00 【sqjddb】
* Recursion and divide and conquer strategy
>> The basic idea of recursion and divide and conquer
Sometimes it is difficult to solve a big problem directly , The idea of divide and conquer is : Divide the big problem into smaller ones , In order to break each one , Divide and rule . Apply divide and conquer means repeatedly , Make the sub problem smaller , The solution of the subproblem is usually the same as that of the original problem , Naturally leads to recursive processes . Divide and conquer and recursion are twin brothers , Many efficient algorithms have been produced .
>> The advantages and disadvantages of recursion

>> Conditions for the application of divide and conquer
The problems that can be solved by divide and conquer generally have the following characteristics :
• The problem can be easily solved by reducing its scale to a certain extent
• The problem can be divided into several smaller problems of the same size
• The solution of the subproblem can be combined into the solution of the problem
• The subproblems are independent of each other , I.e. Zi Wen
There are no common sub problems between the questions
>> The idea of balanced subproblem

>> Recursive classic program


①Ackerman function
Ackerman function A(n,m) There are two independent integer variables m>=0,n>=0, Its definition is as follows
A(1,0)=2;
A(0,m)=1 m>=0
A(n,0)=n+2 n>=2
A(n,m)=A(A(n-1,m),m-1) n,m>=1
This is a double recursive function  A(n,m) Each independent variable of defines a univariate function . The third form of recursion defines the function “ Add 2”.
A(n,m) Each independent variable of defines a univariate function . The third form of recursion defines the function “ Add 2”.
m=1 when , because A(1,1)=A(A(0,1),0)=A(1,0)=2
as well as A(n,1)=A(A(n-1),1),0)=A(n-1,1)+2 (n>1), therefore A(n,1)=2n (n>=1), namely A(n,1) Defined the function “ ride 2”
When m=2 when , because A(1,2)=A(A(0,2),1)=A(1,1)=2
A(n,2)=A(A(n-1,2),1)=2A(n-1,2), therefore A(n,2)=2^n
And so on 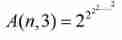
among 2 The number of layers is n.
A(n,4) The growth rate of has become unimaginably fast , It is impossible to write a general term formula to express this function
② The total permutation problem
Design a recursive algorithm to generate n Elements {r1,r2,…,rn} The whole arrangement
R={1,2,3,4}
Output :1234 1243 1324 …… 4312 4132 4123
The procedure is as follows :
Template<class type>
void Perm(Type list[ ], int k, int m)
{
if (k==m)
{
for (int i=0;i<=m;i++)
cout<<list[i];
cout<<endl;
}
else
for(i=k;i<=m;i++)
{
Swap(list[k],list[i]);
Perm(list,k+1,m);
Swap(list[k],list[i]);
}
}
Core statement :
Swap(list[k],list[i]);
Perm(list,k+1,m);
Swap(list[k],list[i]);

The process is tedious , Thinking about the meaning of recursion is of great help in clarifying ideas
③ Integer partition problem
Integer partition problem : Put a positive integer n Expressed as the sum of several positive integers
n=n1+n2+…+nk, n1≥n2≥…≥nk≥1, k≥1
Find out how many ways to divide :
 The procedure is as follows :
The procedure is as follows :
int a(int n, int m)
{
if((n<1) or (m<1))
return 0;
if((n==1) or (m==1))
return 1;
if(n<m)
return q(n,n);
if(n==m)
return q(n,m-1)+1;
return q(n,m-1)+q(n-m,m);
}
④ The hanotta problem
Take the example of Hanoi tower to explain the recursive idea 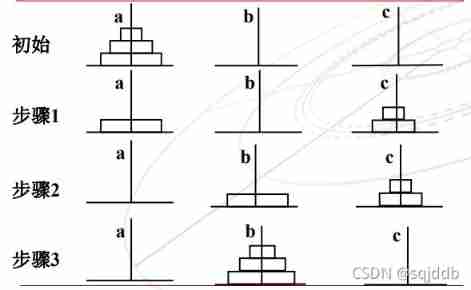
So the core code has three lines , Explain the following :
// Parameter means : hold A Move to according to the rules on B On ,C For the auxiliary tower
Void Hanoi(int n, int A, int B, int C)
{
if(n>0)
{
Hanoi(n-1,A,C,B); // hold n-1 From the A Move to C,B For the auxiliary tower
Move(n,A,B); // Take the biggest one from A Move to B
Hanoi(n-1, C,B,A); // hold n-1 From the C Move to B,A For the auxiliary tower
}
}
Actually Tower of Hanoi's non recursive program It's also worth learning
>> Deep understanding of divide and conquer
The time complexity of the algorithm :
Want to deeply understand the time complexity of the algorithm , Readers are advised to make clear Algorithm time complexity The calculation method of
Good article recommends  The following examples analyze the time complexity of the algorithm , Understand the above k,m The meaning of
The following examples analyze the time complexity of the algorithm , Understand the above k,m The meaning of
① Two point search
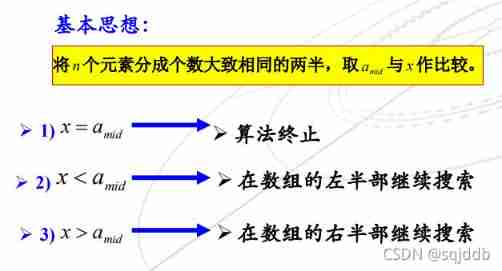


The loop is executed O(logn) Time , The comparison operation in each cycle requires O(1) Time 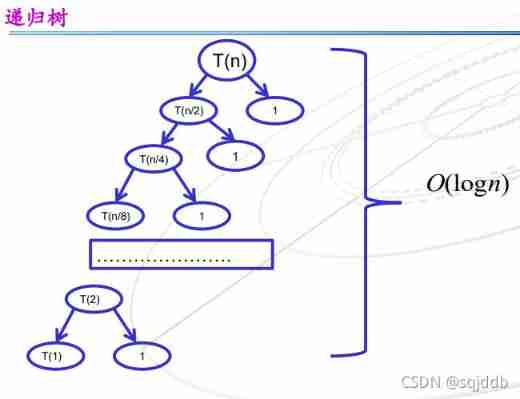
Recursive tree drawing 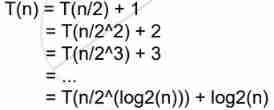

② Multiplication of large integers

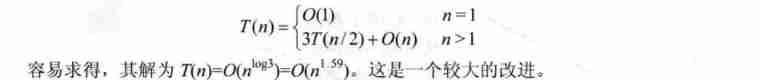 The procedure is as follows :
The procedure is as follows :
③Strassen Matrix multiplication
Matrix multiplication :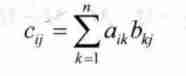
 To reduce time complexity , Made such an attempt :
To reduce time complexity , Made such an attempt :
Strassen To reduce the time complexity

④ Chessboard coverage
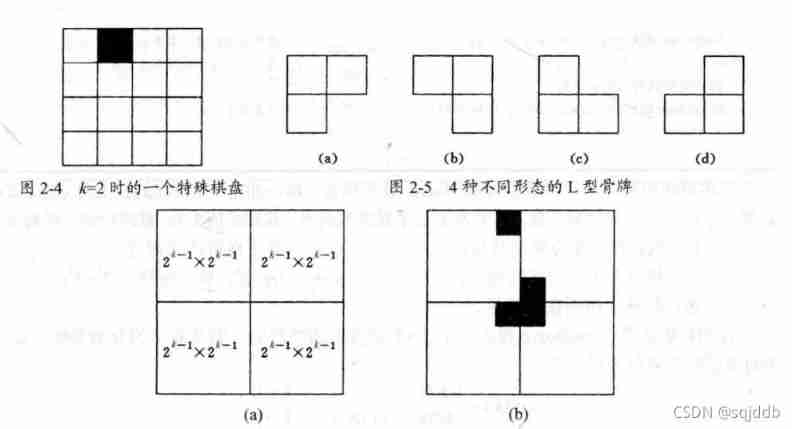


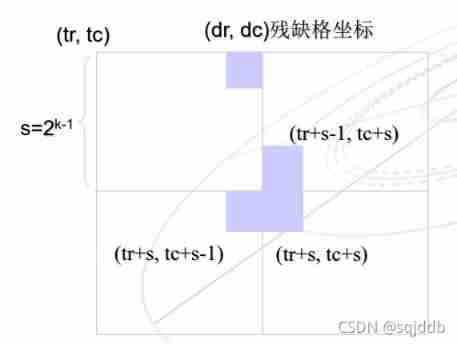
The procedure is as follows : Be careful :tile Global variable
Be careful :tile Global variable
Complexity analysis :
边栏推荐
- Two way process republication + routing policy
- Reprint: summation formula of proportional series and its derivation process
- Histogram equalization
- leetcode1-3
- 基于线性函数近似的安全强化学习 Safe RL with Linear Function Approximation 翻译 1
- What is devsecops? Definitions, processes, frameworks and best practices for 2022
- Exercise 9-1 time conversion (15 points)
- Hands on deep learning (37) -- cyclic neural network
- What are the advantages of automation?
- Whether a person is reliable or not, closed loop is very important
猜你喜欢
【FAQ】华为帐号服务报错 907135701的常见原因总结和解决方法
DML statement of MySQL Foundation

Number of relationship models

The time difference between the past time and the present time of uniapp processing, such as just, a few minutes ago, a few hours ago, a few months ago

基于线性函数近似的安全强化学习 Safe RL with Linear Function Approximation 翻译 1
Rhcsa day 10 operation

Hands on deep learning (42) -- bi-directional recurrent neural network (BI RNN)
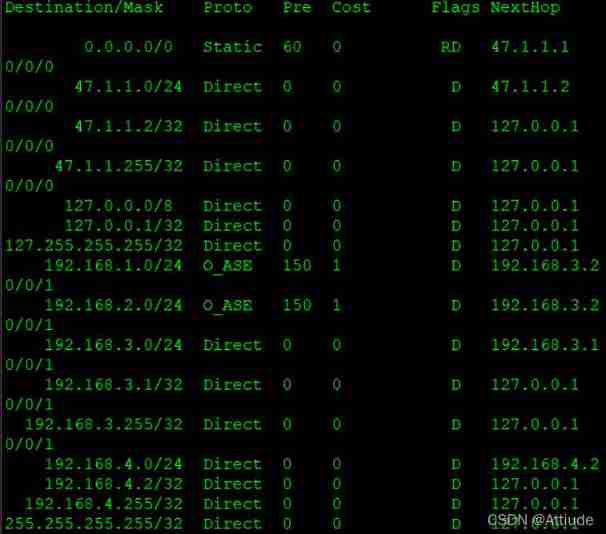
MPLS: multi protocol label switching
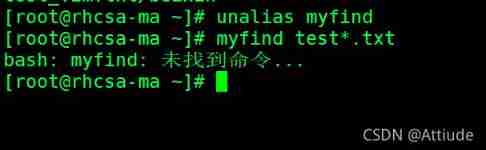
Rhcsa day 9
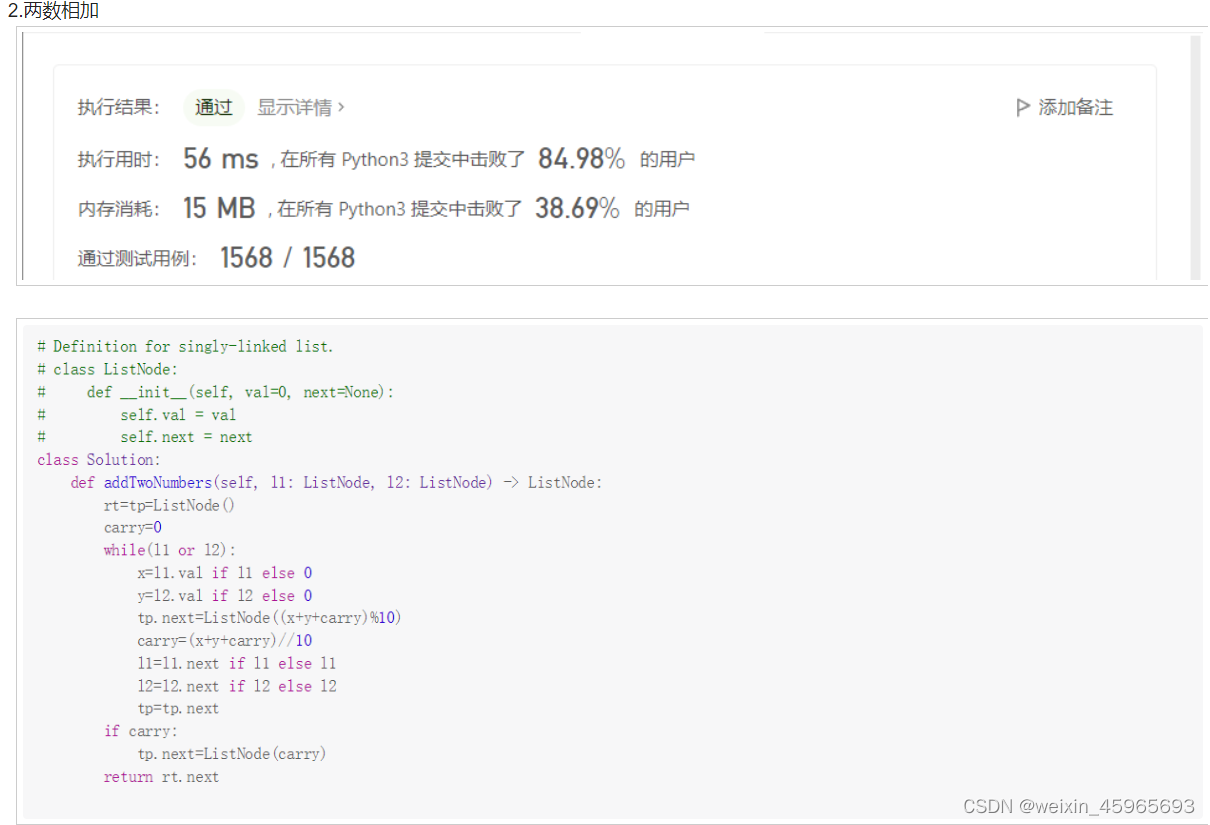
leetcode1-3
随机推荐
Basic principle of servlet and application of common API methods
Rhsca day 11 operation
Safety reinforcement learning based on linear function approximation safe RL with linear function approximation translation 2
Exercise 7-8 converting strings to decimal integers (15 points)
SQL replying to comments
Hands on deep learning (39) -- gating cycle unit Gru
Idea SSH channel configuration
Introduction to extensible system architecture
Vanishing numbers
按键精灵跑商学习-商品数量、价格提醒、判断背包
【Day1】 deep-learning-basics
Latex arranges single column table pictures in double column format articles
How to teach yourself to learn programming
C language structure to realize simple address book
Hands on deep learning (45) -- bundle search
Delayed message center design
The future education examination system cannot answer questions, and there is no response after clicking on the options, and the answers will not be recorded
Intelligent gateway helps improve industrial data acquisition and utilization
Check 15 developer tools of Alibaba
2021-08-10 character pointer
