当前位置:网站首页>Cf960g - bandit Blues (type I Stirling number +ogf)
Cf960g - bandit Blues (type I Stirling number +ogf)
2022-07-06 19:37:00 【Wonderful sauce with pepper】
The question : Find how many are of length n Permutation , Meet the requirement of fetching data from left to right , obtain a Number , Take data from right to left , obtain b individual , The definition of fetching is : If the latter is larger than the current number, replace the current number . Yes 998244353 modulus .
Ideas : Change the meaning of the question , Is to be satisfied a Different prefix maximum 、b The number of permutations of the maximum values of different suffixes .
\qquad Think backwards , The last step must be to take n, therefore n There is a-1 Different prefix maximum , In the back b-1 Maximum suffixes . The two are essentially the same .
Ideas 1 : set up f[i][j] by i The arrangement of numbers is j The number of permutations with different prefix maxima , There's a transfer equation f[i][j] = f[i-1][j-1] + (i-1)*f[i-1][j],f[0][0]=1 It is found that the recurrence formula is the same as that of the first kind of Stirling number
a n s = ∑ i = 0 n − 1 f [ i ] [ a − 1 ] ∗ f [ n − 1 − i ] [ b − 1 ] ∗ C ( n − 1 , i ) ans = \sum_{i=0}^{n-1} f[i][a-1]*f[n-1-i][b-1] * C(n-1,i) ans=∑i=0n−1f[i][a−1]∗f[n−1−i][b−1]∗C(n−1,i), In the sense of Stirling number of the first kind , The expression means , front i The number makes up a-1 Rotation , after n-1-i The number makes up b-1 Rotation , Number of permutation schemes .
Equivalent to n-1 The number makes up a+b-2 Number of rotation schemes ,
namely ans = f[n-1][a+b-2]*C(a+b-2,a-1)
The combination number will be found , The first kind of Stirling number needs to be solved quickly
Because the generating function of the first kind of Stirling number ∑ i = 0 n [ n i ] x i = ∏ i = 0 n − 1 ( x + i ) \sum_{i=0}^n{\left[\begin{matrix}n\\i\end{matrix}\right]}x^i=\prod_{i=0}^{n-1}(x+i) ∑i=0n[ni]xi=∏i=0n−1(x+i), Divide and conquer NTT,O(nlog^n2) Find the Stirling number , Note that what is required here is [ n − 1 a + b − 2 ] \left[\begin{matrix}n-1\\a+b-2\end{matrix}\right] [n−1a+b−2]( Convolution can be done by increasing or decreasing times nlogn seek , I can't compare dishes qaq
Ideas 2: The first equation is difficult to see as Stirling number , Think directly in the mathematical sense .
Yes a-1 Different prefix maximum ,b-1 Different suffix maximum , except a+b-2 The position is fixed , The value of other positions is limited to a certain range , You can take whatever you like , For example, requirements 4 The number provides a maximum of 4 The contribution of , Then the legal arrangement is [4,1,2,3],[4,1,3,2],[4,2,1,3],[4,2,3,1],[4,3,1,2],[4,3,2,1], If one is required 2 And 4 The contribution of , There is only one [2,1,4,3]. That is to say , Yes k Different prefix maximum , Equivalent to k Rotation ([4,1,2,3] <=>[1,2,3,4] After each arrangement is rotated, the maximum value must be placed first ), The problem turns into n-1 The number makes up a+b-2 Number of rotation schemes , Then I did it one by one with the idea .( More abstract )
Pay attention to the situation that must not exist .
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define IOS ios::sync_with_stdio(false),cin.tie(0)
#define _for(i,a,b) for(int i=(a) ;i<=(b) ;i++)
#define _rep(i,a,b) for(int i=(a) ;i>=(b) ;i--)
#define mst(v,s) memset(v,s,sizeof(v))
#define pii pair<int ,int >
#define pb(v) push_back(v)
#define all(v) v.begin(),v.end()
#define int long long
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define endl "\n"
#define fi first
#define se second
#define ls p<<1
#define rs p<<1|1
#define lson p<<1,l,mid
#define rson p<<1|1,mid+1,r
#define AC return 0
#define ldb long double
const int maxn = 6e6+10;
const int p = 998244353;
int Pow(int x,int d){
int tans = 1;
if(d == 0)return 1%p;
int a = Pow(x,d/2);
tans = 1ll*a*a%p;
if(d%2)tans = 1ll*tans*x%p;
return tans%p;
}
typedef vector<int> Poly;// Polynomial definition
int F1[maxn],F2[maxn];
int rev[maxn];
void NTT(int * A,int lim,int opt) {
int i, j, k, m, gn, g, tmp;
for(int i = 0; i < lim; ++i)rev[i] = (i & 1)*(lim >> 1) + (rev[i >> 1] >> 1);
for(i = 0; i < lim; ++i)if (rev[i] < i) swap(A[i], A[rev[i]]);
for(m = 2; m <= lim; m <<= 1) {
k = m >> 1;
gn = Pow(3,(p - 1) / m);
for(i = 0; i < lim; i += m) {
g = 1;
for (j = 0; j < k; ++j, g = 1ll * g * gn % p) {
tmp = 1ll * A[i + j + k] * g % p;
A[i + j + k] = (A[i + j] - tmp + p) % p;
A[i + j] = (A[i + j] + tmp) % p;
}
}
}
if(opt == -1){
reverse(A+1,A+lim);
int inv = Pow(lim,p-2);
for(i = 0; i < lim; ++i) A[i] = 1ll * A[i] * inv % p;
}
}
Poly mul(const Poly & A,const Poly & B){
int n = A.size(),m = B.size();
int siz = n + m - 1;
Poly C(siz);
if(siz < 64){
// Less than or equal to 64 Direct violence counts
for(int i = 0;i < n;i++){
for(int j = 0;j < m;j++)C[i+j] = (C[i+j] + 1LL*A[i]*B[j]%p)%p;
}
return C;
}
int fsiz = 1;
while(fsiz <= siz)fsiz *= 2;
for(int i = 0;i < fsiz;i++)F1[i] = F2[i] = 0;
for(int i = 0;i < n;i++)F1[i] = A[i];
for(int i = 0;i < m;i++)F2[i] = B[i];
NTT(F1,fsiz,1);
NTT(F2,fsiz,1);
for(int i = 0;i < fsiz;i++)F1[i] = 1ll*F1[i]*F2[i]%p;
NTT(F1,fsiz,-1);
for(int i = 0;i < siz;i++){
C[i] = F1[i];
}
return C;
}
int n,A,B;
int fac[100005],ni_f[100005];
Poly cal(int l ,int r){
if( l==r ){
Poly ans(2,0);
ans[0] = l;
ans[1] = 1;
return ans;
}
int mid = (l+r)>>1;
return mul(cal(l,mid),cal(mid+1,r));
}
ll qsm(int a,int b,int mod){
a %= mod;
int ans = 1,temp = a;
while(b){
if( b&1 ) ans = (ans * temp)%mod;
temp = (temp * temp)%mod;
b>>=1;
}
return ans;
}
ll C(int n,int m){
return fac[n]*ni_f[n-m]%p*ni_f[m]%p;
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
IOS;
cin>>n>>A>>B;
if( A==0 || B==0 || A+B-2>n-1){
return cout<<0<<endl,0;
}
if( n==1 ){
return cout<<1<<endl,0;
}
Poly f(n+1,0);
f = cal(0,n-2);
fac[0]=1;
_for(i,1,100000) fac[i] = fac[i-1]*i%p;
ni_f[100000] = qsm(fac[100000],p-2,p);
_rep(i,100000-1,0) ni_f[i] = ni_f[i+1] * (i+1)%p;
int ans = C(A+B-2,A-1) * f[A+B-2]%p;
cout<<ans<<endl;
AC;
}
边栏推荐
- short i =1; I=i+1 and short i=1; Difference of i+=1
- LeetCode_ Double pointer_ Medium_ 61. rotating linked list
- GCC [7] - compilation checks the declaration of functions, and link checks the definition bugs of functions
- Sanmian ant financial successfully got the offer, and has experience in Android development agency recruitment and interview
- Teach you to learn JS prototype and prototype chain hand in hand, a tutorial that monkeys can understand
- MATLAB中deg2rad和rad2deg函数的使用
- 【翻译】云原生观察能力微调查。普罗米修斯引领潮流,但要了解系统的健康状况仍有障碍...
- 企业精益管理体系介绍
- short i =1; i=i+1与short i=1; i+=1的区别
- 1805. 字符串中不同整数的数目
猜你喜欢

Mathematical knowledge -- code implementation of Gaussian elimination (elementary line transformation to solve equations)
![[translation] linkerd's adoption rate in Europe and North America exceeded istio, with an increase of 118% in 2021.](/img/09/106adc222c06cbd2f4f66cf475cce2.jpg)
[translation] linkerd's adoption rate in Europe and North America exceeded istio, with an increase of 118% in 2021.
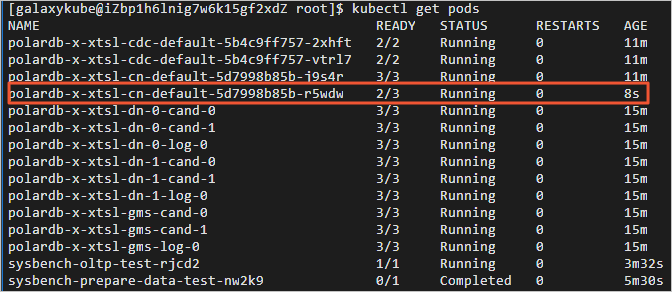
零基础入门PolarDB-X:搭建高可用系统并联动数据大屏
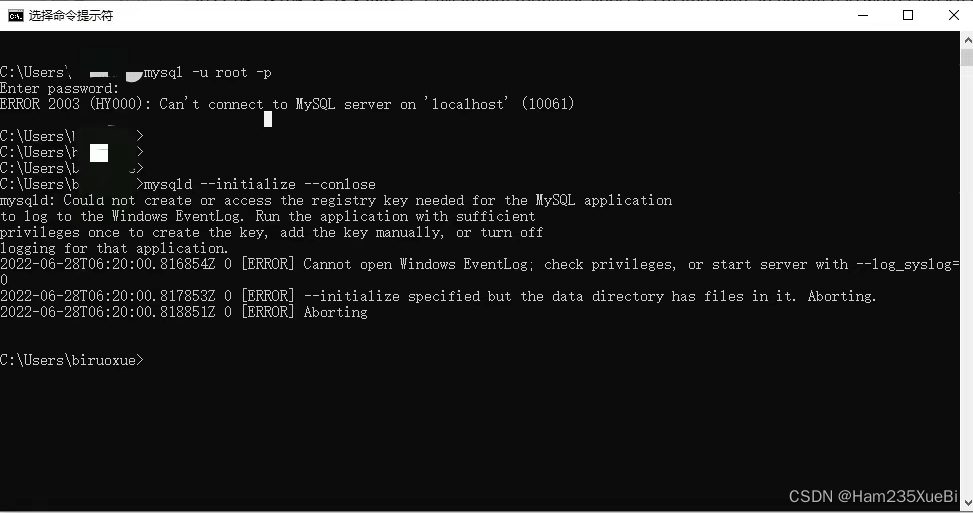
An error occurs when installing MySQL: could not create or access the registry key needed for the

CPU负载很低,loadavg很高处理方法
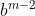
快速幂模板求逆元,逆元的作用以及例题【第20届上海大学程序设计联赛夏季赛】排列计数
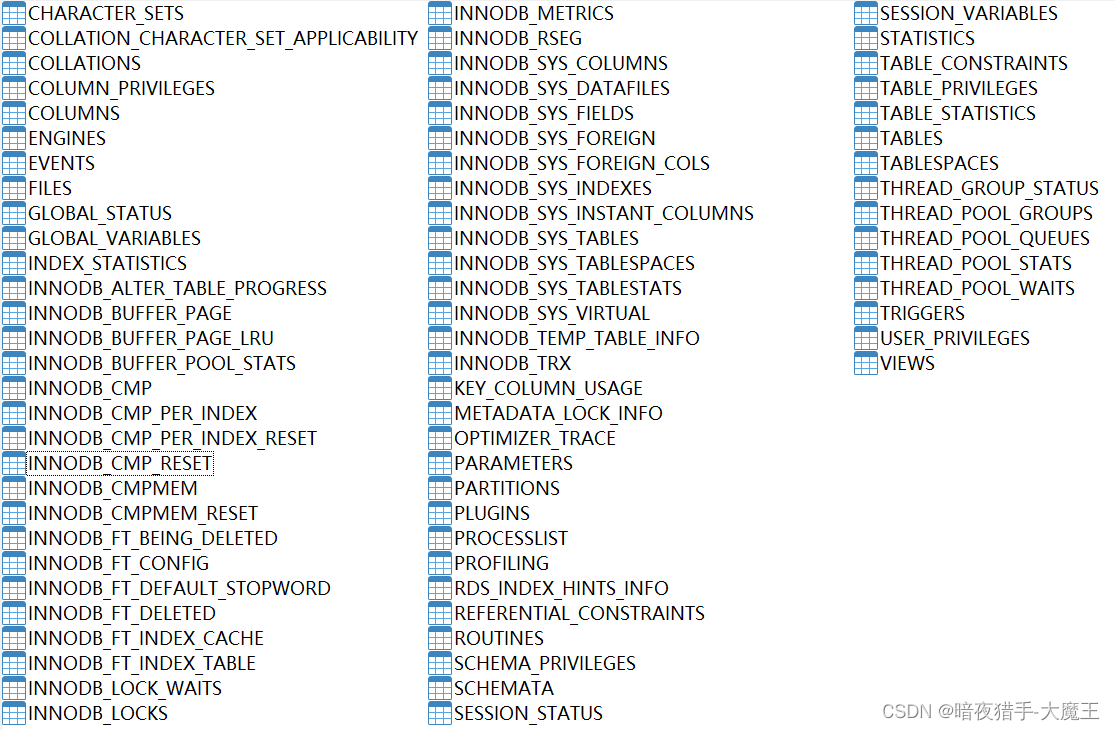
Mysql Information Schema 学习(一)--通用表

黑马--Redis篇

Reflection and illegalaccessexception exception during application

学习探索-使用伪元素清除浮动元素造成的高度坍塌
随机推荐
MRO industrial products enterprise procurement system: how to refine procurement collaborative management? Industrial products enterprises that want to upgrade must see!
spark基础-scala
安装Mysql报错:Could not create or access the registry key needed for the...
【翻译】云原生观察能力微调查。普罗米修斯引领潮流,但要了解系统的健康状况仍有障碍...
Translation D28 (with AC code POJ 26:the nearest number)
ZABBIX proxy server and ZABBIX SNMP monitoring
Don't miss this underestimated movie because of controversy!
Analysis of rainwater connection
LeetCode-1279. Traffic light intersection
凤凰架构3——事务处理
Mysql Information Schema 學習(一)--通用錶
Teach you to learn JS prototype and prototype chain hand in hand, a tutorial that monkeys can understand
Computer network: sorting out common network interview questions (I)
How to customize animation avatars? These six free online cartoon avatar generators are exciting at a glance!
利用 clip-path 绘制不规则的图形
Elastic search indexes are often deleted [closed] - elastic search indexes gets deleted frequently [closed]
Systematic and detailed explanation of redis operation hash type data (with source code analysis and test results)
Unbalance balance (dynamic programming, DP)
Mathematical knowledge -- code implementation of Gaussian elimination (elementary line transformation to solve equations)
LeetCode_格雷编码_中等_89.格雷编码