当前位置:网站首页>第三章 标准单元库(上)
第三章 标准单元库(上)
2022-08-04 05:30:00 【KuoGavin】
文章目录
本章介绍库(library)里单元描述中所提供的时序信息。单元可以是标准单元、IO缓冲器或者是如USB内核这样的复杂IP。
- 除时序信息外,库单元描述中还包含一些其它属性,例如单元面积和功能,这些属性与时序无关,但在RTL综合(synthesis)过程中会用到。在本章中,我们仅关注与时序和功耗计算有关的那些属性。
- 可以使用各种标准格式来描述库单元,各种格式的内容基本相似,本书中使用Liberty语法描述库单元。
- 本章前面部分介绍了线性和非线性时序模型,随后介绍了用于纳米技术的高级时序模型,这些将在3.7节中进行介绍。
3.1 引脚电容(pin capacitance)
单元的每个输入和输出都可以在引脚(pin)上指定电容。在大多数情况下,仅为单元输入引脚指定电容,而不为输出引脚指定电容,即大多数单元库中的输出引脚电容为0。
pin(INP1) {
capacitance:0.5;
rise_capacitance:0.5;
rise_capacitance_range:(0.48, 0.52);
fall_capacitance:0.45;
fall_capacitance_range:(0.435, 0.46);
...
}
上面的示例展示了输入INP1引脚电容值的一般规格(specification)。在最基本的格式中,引脚电容被指定为单个值(在上面的示例中为0.5个单位)。电容单位通常为皮法拉(pF),一般在库文件的开头指定。单元描述中还可以为rise_capacitance(0.5个单位)和fall_capacitance(0.45个单位)分别指定值,这些值是指引脚INP1上发生电平上升和下降转换(transition)时的值。也可以将rise_capacitance和fall_capacitance的值指定为范围,并在描述中指定下限值和上限值。
3.2 时序模型(timing modeling)
逻辑单元的时序模型(timing model)旨在为设计中的各种单元实例(instance)提供准确的时序信息。通常会从单元的详细电路仿真中获得时序模型,用以对单元工作时的实际情况进行建模,且需要为逻辑单元的每个时序弧都建立一个时序模型。
先来考虑简单逻辑单元反相器的时序弧,如下图,其中其输入引脚的上升(下降)沿造成输出针脚的下降(上升)沿。这两种时延分别对应于 T f T_f Tf(output fall delay)和 T r T_r Tr(output rise delay)。

注意,延迟是根据单元库中定义的阈值(threshold)点测量的,通常为50% V d d V_{dd} Vdd。 因此,延迟值指从输入经过其阈值点到输出经过其阈值点的延迟。
通过反相器的时序弧的延迟取决于两个因素:
- 输出负载,即反向器输出针脚上的电容负载;
- 输入信号的过渡时间(transition time);
延迟值与负载电容有单调关系:负载电容 ↑ \uparrow ↑,延迟值 ↑ \uparrow ↑;
延迟值与过渡时间的关系不定:多数情况下,过渡时间 ↑ \uparrow ↑,延迟值 ↑ \uparrow ↑;某些情况下,输入信号阈值点(用于测量延迟)与单元的内部开关点(switching point)明显不同,此时通过单元的延迟可能相对于输入信号过渡时间表现出非单调行为:过渡时间 ↑ \uparrow ↑,延迟值 ↓ \downarrow ↓,尤其负载电容值较小的情况下。
逻辑单元输出引脚的压摆(slew)主要取决于输出引脚的输出电容:输出信号过渡时间会随着输出负载的增加而增加。因此,在输入端压摆时间(压摆是模电中概念,过渡时间是数电中概念)较大(过渡时间较长,理解即可不必纠结)情况下,选择合适的单元类型及输出负载,可以改善输出端的压摆。如下图所示,(b)由于更大的负载,所以压摆就很大。

3.2.1 线性时序模型(linear timing model)
一个简单的时序模型是线性延迟模型(linear delay model),该模型使用含两个参数的线性函数表示逻辑单元的延迟和输出过渡时间,这两个参数是:输入过渡时间(input transition time)和输出负载电容(output load capacitance)。通过逻辑单元的延迟( D D D)使用线性模型的一般形式如下所示:
D = D 0 + D 1 ∗ S + D 2 ∗ C D=D_0+D_1*S+D_2*C D=D0+D1∗S+D2∗C
其中 D 0 D_0 D0, D 1 D_1 D1, D 2 D_2 D2是常数, S S S是输入过渡时间, C C C是输出负载电容。 对于亚微米(submicron)技术,线性延迟模型在输入过渡时间和输出负载电容的范围内并不准确,因此,目前大多数单元库都使用更复杂的模型,例如非线性延迟模型(non-linear delay model)。
3.2.2 非线性时序模型(non-linear timing model)
大多数单元库都包括表格模型(table model),用于为单元的各种时序弧指定延迟并进行时序检查。一些用于纳米技术的较新的时序库还提供了基于电流源的高级时序模型(例如CCS,ECSM等),本章稍后将对此进行介绍。 这些表格模型被称为NLDM(Non-Linear Delay Model),可用于延迟、输出压摆计算或其他时序检查。表格模型中提供了:在单元输入引脚处输入过渡时间和输出引脚处输出负载电容的各种组合下通过单元的延迟。
NLDM模型以二维形式表示,两个独立变量是输入过渡时间和输出负载电容,表中的数值表示延迟。以下是一个典型反相器单元的表格模型示例:
pin (OUT) {
max_transition : 1.0;
timing() {
related_pin : "INP1";
timing_sense : negative_unate;
cell_rise(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7"); /* Input transition */
index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
values ( /* 0.16 0.35 1.43 */ \
/* 0.1 */ "0.0513, 0.1537, 0.5280", \
/* 0.3 */ "0.1018, 0.2327, 0.6476", \
/* 0.7 */ "0.1334, 0.2973, 0.7252");
}
cell_fall(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7"); /* Input transition */
index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
values ( /* 0.16 0.35 1.43 */ \
/* 0.1 */ "0.0617, 0.1537, 0.5280", \
/* 0.3 */ "0.0918, 0.2027, 0.5676", \
/* 0.7 */ "0.1034, 0.2273, 0.6452");
}
上面的示例描述了输出引脚OUT的延迟信息。单元描述里的这个部分包含了从引脚INP1到引脚OUT时序弧的上升和下降延迟模型,以及引脚OUT的max_transition允许时间。上升和下降延迟有单独的模型(models)(用于输出引脚),分别标记为cell_rise和cell_fall。索引(indices) 变量的类型和顺序在以下查找表模板(lookup table template)delay_template_3x3中进行了描述:
lu_table_template(delay_template_3x3) {
variable_1 : input_net_transition;
variable_2 : total_output_net_capacitance;
index_1 ("1000, 1001, 1002"); //index_1 ("0.1, 0.3, 0.7");
index_2 ("1000, 1001, 1002"); //index_2 ("0.16, 0.35, 1.43");
//the above data such as 1000 is dummy placeholder.
//the annonated data is the actual data can be altered in
//models or just be specified in template table.
}/* The input transition and the output capacitance can be in either order, that is, variable_1 can be the output capacitance. However, these designations are usually consistent across all templates in a library. */
可以当作for循环嵌套,index_1(输入过渡时间)和index_2(总输出网络电容,即输出负载电容)均有三个可能值,所以对应的应当是 3 × 3 3\times 3 3×3的表格。对于表格索引值的设定,可以通过两种方法:
- 上述模板表中索引值(e.g. 1000)是伪占位符(dummy placeholder),可在
cell_fall或cell_rise延迟表中实际索引值进行覆盖; - 在模板定义中指定索引值,类似于默认值的设定;
根据延迟表,输入下降过渡时间为0.3ns且输出负载为0.16pf时,反相器的上升延迟为0.1018ns。 由于输入的下降沿跳变导致反相器输出的上升沿跳变,因此当输入引脚发生下降沿跳变时,应该去查询cell_rise延迟表。
将表格中的延迟值表示为输入过渡时间和输出负载电容这两个变量的函数的这种形式称为非线性延迟模型,因为在这些表格中可以看到延迟随输入过渡时间和输出负载电容的非线性变化。
注意,表格模型也可以是3维的,例如一个具有互补输出Q和QN的触发器,这将在3.8节中进行介绍。
NLDM模型不仅可以用于计算延迟,而且还可用于计算逻辑单元输出引脚的过渡时间,该时间同样由输入过渡时间和输出负载电容来表征。因此,还存在着另外一张独立的用于计算单元的输出上升和下降过渡时间的二维表格。
pin (OUT) {
max_transition : 1.0;
timing() {
related_pin : "INP";
timing_sense : negative_unate;
rise_transition(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7"); /* Input transition */
index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
values ( /* 0.16 0.35 1.43 */ \
/* 0.1 */ "0.0417, 0.1337, 0.4680", \
/* 0.3 */ "0.0718, 0.1827, 0.5676", \
/* 0.7 */ "0.1034, 0.2173, 0.6452");
}
fall_transition(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7"); /* Input transition */
index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
values ( /* 0.16 0.35 1.43 */ \
/* 0.1 */ "0.0817, 0.1937, 0.7280", \
/* 0.3 */ "0.1018, 0.2327, 0.7676", \
/* 0.7 */ "0.1334, 0.2973, 0.8452");
}
. . .
}
. . .
}
这里有两个关于过渡时间的表格:rise_transition和fall_transition。如第二章所述,过渡时间是根据特定的压摆阈值点(通常为电源的10%-90%)测量的。
综上所述,使用NLDM模型的反相器具有下列表格模型:
- Rise delay (上升延迟时间)
- Fall delay (下降延迟时间)
- Rise transition (上升过渡时间)
- Fall transition (下降过渡时间)
假设有这么一个反相器单元,其输入过渡时间和输出负载电容如下图所示。对于15ps的输入(下降)过渡时间和10fF负载,可从cell_rise表中获得输出上升延迟时间,而从cell_fall表中可获得20ps输入(上升)过渡时间和10fF负载下的输出下降延迟时间 。

指定单元逻辑功能为“反相”(invert)的信息可以在时序弧里的timing_sense字段中找到,但在某些情况下如果该字段中未指明,则应该也可从引脚功能(pin function)中推断出。
例如对于反相器单元,时序弧为negative_unate,这表明输出引脚电平跳变方向与输入引脚电平跳变方向相反。因此,在cell_rise表中进行查找时使用的参数是输入引脚的下降过渡时间。
对于未在表中出现的对应的(input transition, out capacitance)对,它们的输出延迟值由二维插值进行求取以得到最终的时序值,一般选择每个维度中两个最接近的表格条目的值进行表格插值。考虑(0.15, 1.16pF)的输出下降时延值,下面从下降时延表格中复制了与二维插值相关的部分:
fall_transition(delay_template_3x3) {
index_1 ("0.1, 0.3 . . .");
index_2 (". . . 0.35, 1.43");
values ( \
". . . 0.1937, 0.7280", \
". . . 0.2327, 0.7676"
. . .
在插值的计算公式中, i n d e x 1 index_1 index1的两个插值值标记为 x 1 x_1 x1和 x 2 x_2 x2; i n d e x 2 index_2 index2的两个插值值标记为 y 1 y_1 y1和 y 2 y_2 y2,这些插值值对应的表格中的数值记为 T 11 T_{11} T11, T 12 T_{12} T12, T 21 T_{21} T21和 T 22 T_{22} T22。若是所需查找的表中值的行列值为 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),那么所查值 T 00 T_{00} T00的插值公式如下:
T 00 = x 20 ∗ y 20 ∗ T 11 + x 20 ∗ y 01 ∗ T 12 + x 01 ∗ y 20 ∗ T 21 + x 01 ∗ y 01 ∗ T 22 T_{00}=x_{20}*y_{20}*T_{11}+x_{20}*y_{01}*T_{12}+\\ \quad \quad x_{01}*y_{20}*T_{21}+x_{01}*y_{01}*T_{22} T00=x20∗y20∗T11+x20∗y01∗T12+x01∗y20∗T21+x01∗y01∗T22
其中:
x 01 = ( x 0 − x 1 ) / ( x 2 − x 1 ) x 20 = ( x 2 − x 0 ) / ( x 2 − x 1 ) y 01 = ( y 0 − y 1 ) / ( y 2 − y 1 ) y 02 = ( y 2 − y 0 ) / ( y 2 − y 1 ) x_{01}=(x_0-x_1)/(x_2-x_1) \\ x_{20}=(x_2-x_0)/(x_2-x_1)\\ y_{01}=(y_0-y_1)/(y_2-y_1)\\ y_{02}=(y_2-y_0)/(y_2-y_1) x01=(x0−x1)/(x2−x1)x20=(x2−x0)/(x2−x1)y01=(y0−y1)/(y2−y1)y02=(y2−y0)/(y2−y1)
以上公式对于内插或是外插均有效。
3.2.3 阈值规格和压摆降额(threshold specifications and slew derating)
压摆值基于标准元件库中的规定的测量阈值点,大多上一代库(0.25 μ m \mu m μm或更老)使用 10 % 10\% 10%和 90 % 90\% 90%作为压摆和过渡时间的测量阈值点。
压摆阈值一般选择与电平波形的线性部分相对应。随着技术的发展,实际电平波形最接近线性的部分一般介于 30 % 30\% 30%到 70 % 70\% 70%点之间。因此,大多数最新一代的时序库指定压摆测量点是 30 % 30\% 30%到 70 % 70\% 70%的电源电平 V d d V_{dd} Vdd。然而,由于之前所测的过渡时间的阈值点多在 10 % 10\% 10%和 90 % 90\% 90%,因此在填充库时,通常将所测得的 30 % 30\% 30%到 70 % 70\% 70%的过渡时间加倍,这由压摆降额系数(slew derating factor)指定,在此且通常为 0.5 0.5 0.5。
压摆测量阈值点为 30 % 30\% 30%到 70 % 70\% 70%且压摆降额系数为 0.5 0.5 0.5(在这里是slew_derate_from_library),等效于测量阈值点为 10 % 10\% 10%和 90 % 90\% 90%。 阈值设置的示例如下:
/* Threshold definitions */
slew_lower_threshold_pct_fall : 30.0;
slew_upper_threshold_pct_fall : 70.0;
slew_lower_threshold_pct_rise : 30.0;
slew_upper_threshold_pct_rise : 70.0;
input_threshold_pct_fall : 50.0;
input_threshold_pct_rise : 50.0;
output_threshold_pct_fall : 50.0;
output_threshold_pct_rise : 50.0;
slew_derate_from_library : 0.5;
如上库表格中的过渡时间设置指定要将过渡时间乘以 0.5 0.5 0.5,以获得相对应的过渡时间。意味着表格中的值(以及相应的索引值)实际上是 10 % 10\% 10%- 90 % 90\% 90%阈值点的测量值。在标定过渡时间值时,首先在 30 % − 70 % 30\%-70\% 30%−70%处测量,再把测量值外插到 10 % 10\% 10%- 90 % 90\% 90%的范围上( ( 70 − 30 ) / ( 90 − 10 ) (70-30)/(90-10) (70−30)/(90−10))。
以下是不同压摆阈值设定的例子:
/* Threshold definitions 20/80/1 */
slew_lower_threshold_pct_fall : 20.0;
slew_upper_threshold_pct_fall : 80.0;
slew_lower_threshold_pct_rise : 20.0;
slew_upper_threshold_pct_rise : 80.0;
/* slew_derate_from_library not specified */
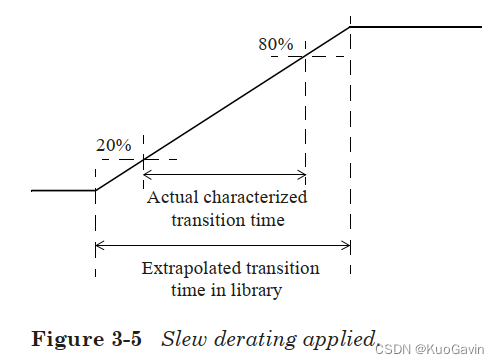
该例是阈值点设置在 20 % − 80 % 20\%-80\% 20%−80%的例子,这里slew_derate_from_library并未设定(默认值为1),说明元件库中的过渡时间并未降额。表格中的过渡时间值直接对应于20%-80%的阈值点,如左下图所示。
 |  |
这里还有个进行降额的例子:
slew_lower_threshold_pct_rise : 20.00;
slew_upper_threshold_pct_rise : 80.00;
slew_lower_threshold_pct_fall : 20.00;
slew_upper_threshold_pct_fall : 80.00;
slew_derate_from_library : 0.6;
在这种情况下,将slew_derate_from_library设置为 0.6 0.6 0.6,并将压摆测量阈值点指定为 20 % − 80 % 20\%-80\% 20%−80%,这意味着库中的过渡时间表里的数据对应于外推到 0 % − 100 % 0\%-100\% 0%−100%( ( 80 − 20 ) / ( 100 − 0 ) = 0.6 (80-20)/(100-0)= 0.6 (80−20)/(100−0)=0.6)的值,如右上图。
指定了压摆降额后,计算延迟时使用的压摆值等于:
计算延迟时使用的压摆值 = 库中过渡时间值 ∗ 压摆降额系数( l i b r a r y _ t r a n s i t i o n _ t i m e v a l u e ∗ s l e w d e r a t e ) 计算延迟时使用的压摆值 = \\库中过渡时间值 * 压摆降额系数 ( library\_transition\_time_value * slew_derate) 计算延迟时使用的压摆值=库中过渡时间值∗压摆降额系数(library_transition_timevalue∗slewderate)
这就是延迟计算工具在内部使用的压摆值,是对应于指定的压摆阈值测量点的。
3.3 时序模型-组合逻辑单元(timing model-combinational logic cells)
考虑两个输入引脚的AND元件的时序弧。该元件的两个时序弧均是正单边的;因此输入针脚的上升沿对应输出针脚的上升沿,反之同理。
对于双端输入的AND元件,有四个时延:
- A → Z : A \rarr Z: A→Z:Output rise(输出上升时延);
- A → Z : A \rarr Z: A→Z:Output fall(输出下降时延);
- B → Z : B \rarr Z: B→Z:Output rise(输出上升时延);
- B → Z : B \rarr Z: B→Z:Output fall(输出下降时延);
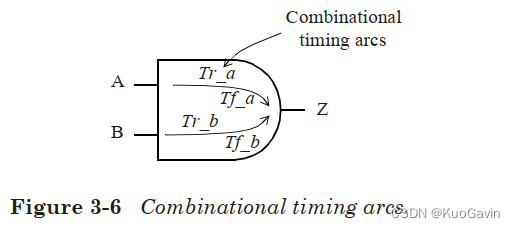
这意味着对于NLDM模型,将会有四个表格模型用于指定延迟。同样,也将有四个表格模型用于指定输出过渡时间(压摆)。
3.3.1 时延和压摆模型(delay and slew models)
对于一个三个输入针脚的NANA与非门元件其输入针脚INP1和输出针脚OUT的指定如下:
pin (OUT) {
max_transition : 1.0;
timing() {
related_pin : "INP1";
timing_sense : negative_unate;
cell_rise(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7");
index_2 ("0.16, 0.35, 1.43");
values ( \
"0.0513, 0.1537, 0.5280", \
"0.1018, 0.2327, 0.6476", \
"0.1334, 0.2973, 0.7252");
}
rise_transition(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7");
index_2 ("0.16, 0.35, 1.43");
values ( \
"0.0417, 0.1337, 0.4680", \
"0.0718, 0.1827, 0.5676", \
"0.1034, 0.2173, 0.6452");
}
cell_fall(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7");
index_2 ("0.16, 0.35, 1.43");
values ( \
"0.0617, 0.1537, 0.5280", \
"0.0918, 0.2027, 0.5676", \
"0.1034, 0.2273, 0.6452");
}
fall_transition(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7");
index_2 ("0.16, 0.35, 1.43");
values ( \
"0.0817, 0.1937, 0.7280", \
"0.1018, 0.2327, 0.7676", \
"0.1334, 0.2973, 0.8452");
}
. . .
}
. . .
}
在上面的例子中,使用了两个单元延迟表cell_rise和cell_fall以及两个过渡时间表rise_transition和fall_transition来描述从INP1到OUT的时序弧的特性,上面的例子中还包括了输出的最大过渡时间(max_transition)值。
与非门单元中的时序弧为负单边类型(negative unate),这表示输出引脚电平跳变方向与输入引脚电平跳变方向是相反的。因此,查找cell_rise表对应于输入引脚上的下降过渡时间。同样,通过与门单元或者或门单元的时序弧是正单边类型(positive unate)的,因为输出引脚电平跳变方向与输入引脚电平跳变方向相同。
3.3.2 通用组合逻辑块(general combinational block)
考虑以下这个具有三输入和两输出的通用组合逻辑块(General Combinational Block):

像这样的组合逻辑块可以具有多个时序弧。通常,从块的每个输入到每个输出都有一条时序弧。如果从输入到输出的逻辑路径是同相(non-inverting)或正单边类型的,则输出的极性(polarity)与输入的极性相同;如果逻辑路径是反相(inverting)或负单边类型,则输出的极性与输入相反,即当输入电平上升时,输出电平将下降。这些时序弧代表了通过这个组合逻辑块的传播延迟。
通过组合逻辑单元的某些时序弧可以既是正单边类型,也是负单边类型的。一个例子是通过两输入异或门(xor)单元的时序弧,根据该单元的另一个输入的逻辑状态,两输入异或门单元的输入引脚处的电平跳变会导致输出引脚处的电平沿相同或相反的方向跳变。这些时序弧可以描述为非单边类型(non-unate)的,也可以描述为两组状态相关(state-dependent)的正单边类型时序模型和负单边类型时序模型。这种与状态相关的表格模型将在下节中有更详细的描述。
3.4 时序模型-序列逻辑单元(timing models-sequential cells)
考虑如下图所示的时序逻辑单元的时序弧:

对于同步(synchronous)输入,比如 D D D针脚(或 S I SI SI, S E SE SE),有如下时序弧:
- 建立(Setup)时间检查时序弧(包括上升沿和下降沿);
- 保持(Hold)时间检查时序弧(包括上升沿和下降沿);
对于异步(asynchronous)输入,例如针脚 C D N CDN CDN,存在以下时序弧:
- 恢复(Recovery)时间检查时序弧;
- 撤销(Removal)时间检查时序弧;
对于触发器的同步输出,例如引脚 Q Q Q或 Q N QN QN,存在以下时序弧:
- 时钟引脚( C K CK CK)到输出端口( Q Q Q或 Q N QN QN)的传播延迟时序弧(包括上升沿和下降沿);
所有同步时序弧均相对于时钟的有效沿(active edge),即时序逻辑单元捕获数据的时钟沿。此外,时钟引脚和异步引脚(如复位引脚)还需要进行脉冲宽度(pulse width)时序检查。各种时序检查如下图所示:

3.4.1 同步检查:建立和保持(synchronous check: setup and hold)
需要进行建立时间和保持时间的同步时序检查,才能确保数据能够正确通过时序单元传播。这些时序检查可验证输入的数据在时钟有效沿上是否为确定的逻辑状态,并且在有效沿上将正确的数据锁存下来。这些时序检查也可以验证输入的数据在有效时钟沿附近是否稳定:
- 建立时间(setup time)指的是输入的数据必须在有效时钟沿之前保持稳定的最短时间。这是根据最晚的(the latest)数据信号超过其阈值(通常为 V d d V_{dd} Vdd的 50 % 50% 50%)到有效时钟沿超过其阈值(通常为 V d d V_{dd} Vdd的 50 % 50% 50%)的时间间隔测量的。
- 保持时间(hold time)是在时钟有效沿之后输入的数据必须保持稳定的最短时间,这也是根据有效时钟沿超过其阈值到最早的(the earliest)数据信号超过其阈值的时间间隔来度量的。
- 时序单元的时钟有效沿是指使时序单元捕获数据的上升沿或下降沿。
建立时间与保持时间检查实例
时序单元同步引脚的建立时间和保持时间约束通常用二维表格来描述,如下所示。下面的例子展示了触发器数据引脚的建立时间和保持时间时序信息:
pin (D) {
direction : input;
. . .
timing () {
related_pin : "CK";
timing_type : "setup_rising";
rise_constraint ("setuphold_template_3x3") {
index_1("0.4, 0.57, 0.84"); /* Data transition */
index_2("0.4, 0.57, 0.84"); /* Clock transition */
values( /* 0.4 0.57 0.84 */ \
/* 0.4 */ "0.063, 0.093, 0.112", \
/* 0.57 */ "0.526, 0.644, 0.824", \
/* 0.84 */ "0.720, 0.839, 0.930");
}
fall_constraint ("setuphold_template_3x3") {
index_1("0.4, 0.57, 0.84"); /* Data transition */
index_2("0.4, 0.57, 0.84"); /* Clock transition */
values( /* 0.4 0.57 0.84 */ \
/* 0.4 */ "0.762, 0.895, 0.969", \
/* 0.57 */ "0.804, 0.952, 0.166", \
/* 0.84 */ "0.159, 0.170, 0.245");
}
}
timing () {
related_pin : "CK";
timing_type : "hold_rising";
rise_constraint ("setuphold_template_3x3") {
index_1("0.4, 0.57, 0.84"); /* Data transition */
index_2("0.4, 0.57, 0.84"); /* Clock transition */
values( /* 0.4 0.57 0.84 */ \
/* 0.4 */ "-0.220, -0.339, -0.584", \
/* 0.57 */ "-0.247, -0.381, -0.729", \
/* 0.84 */ "-0.398, -0.516, -0.864");
}
fall_constraint ("setuphold_template_3x3") {
index_1("0.4, 0.57, 0.84"); /* Data transition */
index_2("0.4, 0.57, 0.84");/* Clock transition */
values( /* 0.4 0.57 0.84 */ \
/* 0.4 */ "-0.028, -0.397, -0.489", \
/* 0.57 */ "-0.408, -0.527, -0.649", \
/* 0.84 */ "-0.705, -0.839, -0.580");
}
}
}
以上实例展示了相对于时序单元时钟引脚 C K CK CK的上升沿,在输入引脚 D D D上的建立时间和保持时间约束。二维表格模型是根据约束引脚constrained_pin(D)和相关引脚related_pin(CK)处的过渡时间确定得,而查找是基于库中描述得模板setuphold_template_3x3。对于上述实例,模板的实例如下:
lu_table_template(setuphold_template_3x3) {
variable_1 : constrained_pin_transition;
variable_2 : related_pin_transition;
index_1 ("1000, 1001, 1002");
index_2 ("1000, 1001, 1002");
}
/* The constrained pin and the related pin can be in either order, that is, variable_1 could be the related pin transition. However, these designations are usually consistent across all templates in a library. */
建立时间和保持时间检查里的负值
请注意,上面示例中的某些保持时间值是负数。这是可以接受的,这种情况通常发生在触发器的引脚到数据内部锁存点的路径长于相应的时钟路径时。因此,负的保持时间检查意味着触发器的数据引脚可以在时钟引脚之前改变,并且仍然满足保持时间的检查要求。
触发器的建立时间值也可以为负。这意味着触发器的数据引脚可以在时钟引脚之后改变,并且仍然满足建立时间的检查要求。
建立时间和保持时间不可以均为负数!为使建立时间和保持时间检查相一致,建立时间和保持时间的数值总和应为正。因此,如果建立(或保持)时间检查包含负值,则相应的保持(或建立)时间检查应为正值,且足够大,以使建立时间加上保持时间之和是一个正数。 具有负的保持时间值的示例如下图所示,由于建立时间检查会先于保持时间检查,所以此时的建立时间加上保持时间显然是一个正数。建立时间加上保持时间即为要求数据信号稳定的区域的宽度。

对于触发器,在扫描数据(scan data)输入引脚上设置一个负的保持时间会很有帮助,这样可以给予时钟偏斜(clock skew)一定的灵活性,并且可以消除当扫描模式(scan mode)下保持时间发生违例时插入缓冲器(buffer)的需要(扫描模式是将触发器串联在一起形成一条扫描链的模式,触发器的输出通常连接到串联的下一个触发器的扫描数据输入引脚,这些连接是用于芯片测试的)。
与同步数据输入引脚上的建立时间或保持时间检查类似,对异步引脚进行的时序约束检查将在下个小节中介绍。
3.4.2 异步时序检查(asynchronous checks)
恢复时间(recovery)和撤销时间(removal)检查
诸如异步复位(clear)或异步置位(set)之类的异步引脚会覆盖单元的任何同步行为。当异步引脚处于有效(active)状态时,输出将由异步引脚控制,而不是由时钟锁存到的输入数据控制。但是,当异步引脚变为无效(inactive)状态时,时钟的有效边沿将开始锁存输入的数据。异步恢复(recovery)时间和撤销(removal)时间约束检查将验证异步引脚在下一个时钟有效沿处是否已明确返回到了无效状态。
恢复时间是指异步输入被置为无效(de-asserted)后在下一个时钟有效沿之前需要保持稳定的最短时间。
同样,撤销时间是指在一个有效的时钟沿之后,异步引脚必须保持有效状态的最小时间,即在有效时钟沿之后必须经过一段撤销时间才能够将异步引脚置为无效状态。
异步恢复时间和撤销时间检查将分别在8.6节和8.7节中介绍。
脉冲宽度(pulse width)检查
除了同步和异步时序检查外,还有一项检查去确保逻辑单元输入引脚上的脉冲宽度满足最低要求。例如,如果时钟引脚上的脉冲宽度小于指定的最小值,则时钟可能无法正确锁存数据。也可以为相关的同步和异步引脚指定脉冲宽度检查(pulse width check),并且可以为高脉冲和低脉冲分别指定最小脉冲宽度检查。
恢复时间、撤销时间和脉冲宽度检查示例
下面给出了触发器的异步清零引脚 C D N CDN CDN的恢复时间、撤销时间和脉冲宽度检查的示例,其中恢复时间和撤销时间检查还与时钟引脚 C K CK CK有关。由于恢复时间和撤销时间检查是针对异步引脚被置为无效的时刻,因此在以下示例中仅存在上升约束。 C D N CDN CDN引脚的最小脉冲宽度检查用于低脉冲,这是由于 C D N CDN CDN引脚为低电平有效,因此该引脚上的高脉冲宽度没有限制,因此未指定。
pin(CDN) {
direction : input;
capacitance : 0.002236;
. . .
timing() {
related_pin : "CDN";
timing_type : min_pulse_width;
fall_constraint(width_template_3x1) {
/*low pulse check*/
index_1 ("0.032, 0.504, 0.788"); /* Input transition */
values ( /* 0.032 0.504 0.788 */ \
"0.034, 0.060, 0.377");
}
}
timing() {
related_pin : "CK";
timing_type : recovery_rising;
rise_constraint(recovery_template_3x3) {
/* CDN rising */
index_1 ("0.032, 0.504, 0.788"); /* Data transition */
index_2 ("0.032, 0.504, 0.788"); /* Clock transition */
values( /* 0.032 0.504 0.788 */ \
/* 0.032 */ "-0.198, -0.122, 0.187", \
/* 0.504 */ "-0.268, -0.157, 0.124", \
/* 0.788 */ "-0.490, -0.219, -0.069");
}
}
timing() {
related_pin : "CP";
timing_type : removal_rising;
rise_constraint(removal_template_3x3) {
/* CDN rising */
index_1 ("0.032, 0.504, 0.788"); /* Data transition */
index_2 ("0.032, 0.504, 0.788"); /* Clock transition */
values( /* 0.032 0.504 0.788 */ \
/* 0.032 */ "0.106, 0.167, 0.548", \
/* 0.504 */ "0.221, 0.381, 0.662", \
/* 0.788 */ "0.381, 0.456, 0.778");
}
}
}
3.4.3 传播时延(propagation delay)
时序元件的传播时延指的是从时钟的有效沿到输出的上升/下降沿的时间。以下是一个时钟下降沿触发的触发器从 C K N CKN CKN引脚到输出 Q Q Q引脚传播时延时序弧。该时序弧是非单边的因为时钟的有效沿可以造成输出 Q Q Q的上升沿或是下降沿。如下是时延查找表:
timing() {
related_pin : "CKN";
timing_type : falling_edge;
timing_sense : non_unate;
cell_rise(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7"); /* Clock transition */
index_2 ("0.16, 0.35, 1.43"); /* Output capacitance */
values ( /* 0.16 0.35 1.43 */ \
/* 0.1 */ "0.0513, 0.1537, 0.5280", \
/* 0.3 */ "0.1018, 0.2327, 0.6476", \
/* 0.7 */ "0.1334, 0.2973, 0.7252");
}
rise_transition(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7");
index_2 ("0.16, 0.35, 1.43");
values ( \
"0.0417, 0.1337, 0.4680", \
"0.0718, 0.1827, 0.5676", \
"0.1034, 0.2173, 0.6452");
}
cell_fall(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7");
index_2 ("0.16, 0.35, 1.43");
values ( \
"0.0617, 0.1537, 0.5280", \
"0.0918, 0.2027, 0.5676", \
"0.1034, 0.2273, 0.6452");
}
fall_transition(delay_template_3x3) {
index_1 ("0.1, 0.3, 0.7");
index_2 ("0.16, 0.35, 1.43");
values ( \
"0.0817, 0.1937, 0.7280", \
"0.1018, 0.2327, 0.7676", \
"0.1334, 0.2973, 0.8452");
}
}
同先前的例子一样,输出时延由一个输入过渡时间和输出负载相关的二维表格来表达。然而在此例中,由于触发器是时钟下降沿触发的,输入过渡时间使用的是 C K N CKN CKN引脚的下降沿过渡时间,这里是在如上实例中由timing_type字段指出的,上升沿触发的触发器会将rising_edge指定为其timing_type。
timing() {
related_pin : "CKP";
timing_type : rising_edge;
timing_sense : non_unate;
cell_rise(delay_template_3x3) {
. . .
}
. . .
}
边栏推荐
- yolov3 data reading (2)
- 【论文阅读】Mining Cross-Image Semantics for Weakly Supervised Semantic Segmentation
- 光条中心提取方法总结(一)
- 深度确定性策略梯度(DDPG)
- 【论文阅读】TransReID: Transformer-based Object Re-Identification
- Introduction of linear regression 01 - API use cases
- Copy Siege Lions "sticky" to AI couplets
- 学习资料re-id
- Vision Transformer 论文 + 详解( ViT )
- 亚马逊云科技Build On-Amazon Neptune基于知识图谱的推荐模型构建心得
猜你喜欢
随机推荐
DRA821 环境搭建
典型CCN网络——efficientNet(2019-Google-已开源)
Brief description of database and common operation guide
光条提取中的连通域筛除
审稿意见回复
arm-3-中断体系结构
如何成长为高级工程师?
YOLOV4流程图(方便理解)
动手学深度学习_卷积神经网络CNN
投稿相关
学习资料re-id
亚马逊云科技Build On-Amazon Neptune基于知识图谱的推荐模型构建心得
[CV-Learning] Semantic Segmentation
MNIST手写数字识别 —— 从零构建感知机实现二分类
tensorRT教程——使用tensorRT OP 搭建自己的网络
PCL1.12 解决memory.h中EIGEN处中断问题
lstm pipeline 过程理解(输入输出)
latex-写论文时一些常用设置
[Copy Siege Lion Log] Flying Pulp Academy Intensive Learning 7-Day Punch Camp-Study Notes
深度学习理论 —— 初始化、参数调节


![[CV-Learning] Semantic Segmentation](/img/ad/ff5076495fa68e4bbf3be78f5ac6f2.png)