当前位置:网站首页>【GNSS】抗差估计(稳健估计)原理及程序实现
【GNSS】抗差估计(稳健估计)原理及程序实现
2022-07-06 09:18:00 【Proletarians】
抗差估计
抗差估计的原理
抗差估计是近代测量平差范畴,又名稳健估计(robust estimate),据杨院士说中科院系统喜欢称之为抗差估计,武大喜欢称之为稳健估计。我们的测量值是随机变量,符合正态分布的,如果出现粗差(gross error)的话,我们在应用最小二差或卡尔曼滤波的时候就会使结果偏离真实值(滤波发散)的现象。我们解决粗差或系统误差的时候,可以从两方面去理解,均值漂移或者方差膨胀,抗差估计属于方差膨胀模型,即均值不变,方差变化的现象。我们可以通过对出现粗差的观测值进行降权处理。
我比较懒,不想打公式,大家应该也看过类似的推导,其实公式跟最小二差一样的,变化的地方就是权阵,换成了等价权,那么影响等价权的又是等价权函数,常见的有huber、IGG III等,我推荐IGG III,代码好实现。
我们在实现的时候,这个权阵很重要,权阵也就是我们说的方差阵的逆,分为独立和非独立,即观测值之间是否相关,是否相关也影响着等价权函数的形式。举一个最简单的独立观测距离的例子吧
抗差估计的例子
我们假设对一段距离进行10次独立观测,10个观测值分别为:5.09、5.10、5.13、5.09、5.12、5.08、5.46、7.81、5.10、5.11(单位为m),数据是我随便编的。
从上面这段描述,我们可以知道测量个数n=10,必要观测m=1,多余观测为n-m=9。独立观测那么权阵就是对角线,先验权矩阵为单位对角阵。而且肉眼可见的是7.81这个观测值是粗差,5.46嘛不确定是不是。
抗差程序实现
matlab实现的
%% 功能3-抗差估计
% % 假设对一段长度进行观测,5.09 5.10 5.13 5.09 5.12 5.08 5.46 7.81 5.10 5.11
close all
clear all
clc
k0=1.0;k1=2.5;k=1.0;
B=ones(10,1);% 设计矩阵
l=[5.09 5.10 5.13 5.09 5.12 5.08 6.46 7.81 5.10 5.11]';
% P=diag(ones(10,1));% 先验权矩阵1,等价权
P=diag(1./l);% 先验权矩阵2,根据长度倒数定权
x_prev=0;
x0=5.10;% 赋初值
l=l-x0;
while(1)
W=B'*P*l;
N=B'*P*B;
x=inv(N)*W;% 待估参数向量
v=B*x-l;% 残差向量
sigma0=sqrt(v'*P*v/(10-1));% 单位权中误差
disp(['待估参数向量:',num2str(x),' 单位权中误差:',num2str(sigma0)]);
Q=inv(P);
Qvv=Q-B*inv(N)*B';
for i=1:10
v_=v(i)/(sigma0*sqrt(Qvv(i,i)));
if abs(v_)<=k0
k=1.0;
elseif abs(v_)>k1
k=1e-8;
else
k=(k0/abs(v_))*((k1-abs(v_))/(k1-k0))^2;
end
P(i,i)=P(i,i)*k;
end
if x_prev==0
x_prev=x;
continue;
elseif abs(x_prev-x)<0.01
break;
end
x_prev=x;
end
x=x0+x_prev;%求出的最后长度 初值+改正数
disp(['length is ',num2str(x)])
打印结果如下:
使用等价权结果是:
待估参数向量:0.309 单位权中误差:0.8512
待估参数向量:0.042222 单位权中误差:0.11331
待估参数向量:0.0025 单位权中误差:0.01472
待估参数向量:-0.00031553 单位权中误差:0.0084525
length is 5.1025
使用长度倒数定权结果是:
待估参数向量:0.2218 单位权中误差:0.31128
待估参数向量:0.03985 单位权中误差:0.048702
待估参数向量:0.0024523 单位权中误差:0.0065128
待估参数向量:-0.0003396 单位权中误差:0.0037381
length is 5.1025
图中第一行就是我们最小二乘的结果,10个结果中只有一个结果与最小二乘得出的值接近,很明显与我们测量的结果是不一致的,所以说有一个粗差存在就会对最小二乘的结果产生毁灭性。那么如果我们应用抗差估计的话,再经过3次迭代就得出了最后的结果和单位权中误差。
如果我对第七个值,做修改,即由5.46变成6.46。结果如下所示:
使用单位权结果是:
待估参数向量:0.409 单位权中误差:0.91426
待估参数向量:0.1257 单位权中误差:0.38585
待估参数向量:0.0025 单位权中误差:0.01472
待估参数向量:-0.00031551 单位权中误差:0.0084526
length is 5.1025
使用长度倒数定权结果是:
待估参数向量:0.2218 单位权中误差:0.31128
待估参数向量:0.03985 单位权中误差:0.048702
待估参数向量:0.0024523 单位权中误差:0.0065128
待估参数向量:-0.0003396 单位权中误差:0.0037381
length is 5.1025
结论
使用抗差估计确定提高了参数估值的准确性,另外不同的先验权矩阵在迭代过程中结果是不一致,对于本例中使用长度倒数来定权,无论是否应用最小二差,其结果都与真实值接近,单位权中误差也较小。
观测值相关的抗差估计
主要就是这三步迭代:
1、标准化残差,单位权中误差
2、方差放大因子
3、等价方差
欢迎交流啊~
更新于2020/11/10 14:20:00
在上述例子中,要使用标准化残差,此处感谢中测院的肖同学提醒,很久没看经典平差了,协方差阵传播公式还真忘记了,哈哈哈。
扩展:其实我们在gnss spp中,观测值之间也是不相关的,所以懂了吧,找到对应参数直接套用就行了。
边栏推荐
- Unity场景跳转及退出
- [leetcode19] delete the penultimate node in the linked list
- ORA-02030: can only select from fixed tables/views
- Minio file download problem - inputstream:closed
- MySQL time, time zone, auto fill 0
- Liste des boucles de l'interface graphique de défaillance
- VLSM variable length subnet mask partition tips
- Design and implementation of general interface open platform - (39) simple and crude implementation of API services
- MySQL error warning: a long semaphore wait
- Fabrication d'un sac à dos simple fairygui
猜你喜欢
Teach you to release a DeNO module hand in hand
![[Clickhouse kernel principle graphic explanation] about the collaborative work of partitioning, indexing, marking and compressed data](/img/28/221b0a51ef5f2e8ed5aeca2de8f463.jpg)
[Clickhouse kernel principle graphic explanation] about the collaborative work of partitioning, indexing, marking and compressed data
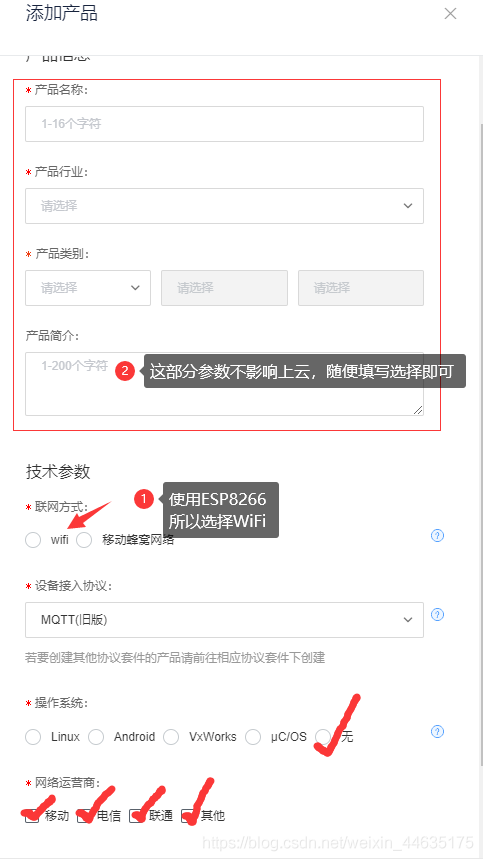
ESP8266连接onenet(旧版MQTT方式)
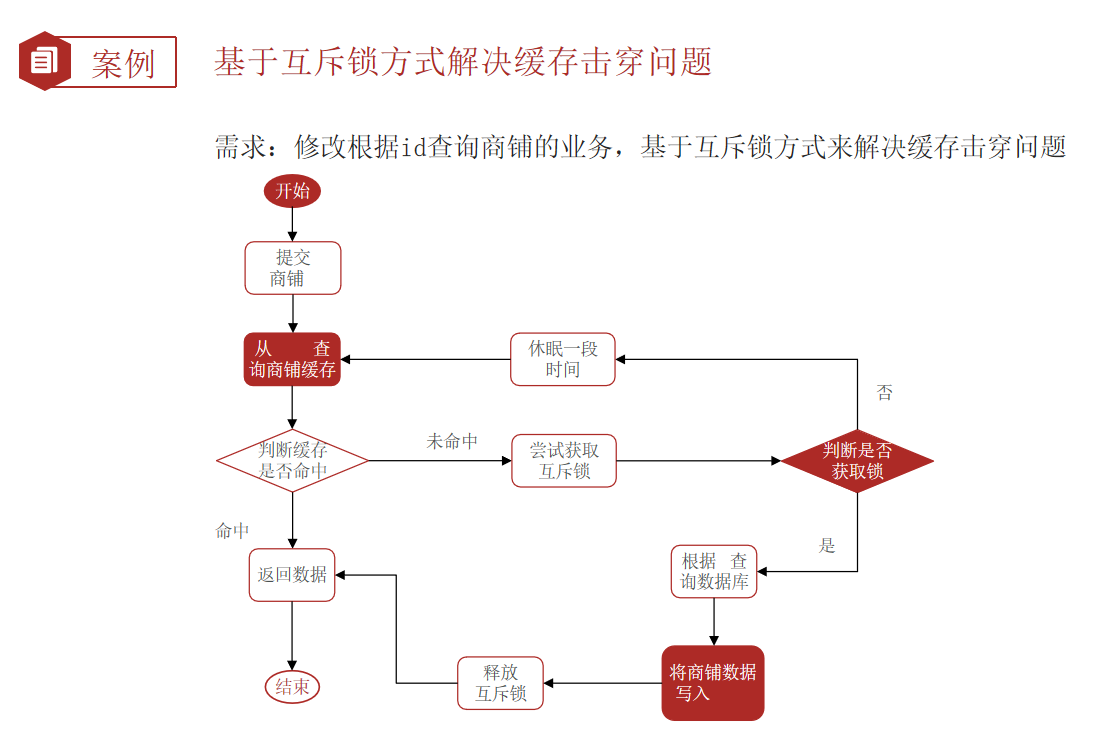
Redis cache update strategy, cache penetration, avalanche, breakdown problems
FairyGUI复选框与进度条的组合使用
Programming homework: educational administration management system (C language)
FairyGUI增益BUFF数值改变的显示
Problèmes avec MySQL time, fuseau horaire, remplissage automatique 0
FairyGUI循环列表

FairyGUI按钮动效的混用
随机推荐
PT OSC deadlock analysis
MySQL takes up too much memory solution
Unity3d makes the registration login interface and realizes the scene jump
How to improve the deletion speed of sequential class containers?
The service robots that have been hyped by capital and the Winter Olympics are not just a flash in the pan
Particle system for introduction to unity3d Foundation (attribute introduction + case production of flame particle system)
First use of dosbox
地球围绕太阳转
Compilation principle: preprocessing of source program and design and implementation of lexical analysis program (including code)
(四)R语言的数据可视化——矩阵图、柱状图、饼图、散点图与线性回归、带状图
关于Gateway中使用@Controller的问题
Liste des boucles de l'interface graphique de défaillance
(1) Introduction Guide to R language - the first step of data analysis
C programming exercise
It has been solved by personal practice: MySQL row size too large (> 8126) Changing some columns to TEXT or BLOB or using ROW_ FORMAT
Esp8266 connect onenet (old mqtt mode)
2021.11.10汇编考试
FGUI工程打包发布&导入Unity&将UI显示出来的方式
MySQL replacement field part content
[offer78] merge multiple ordered linked lists