Number theory --- fast power, fast power inverse element

Fast power

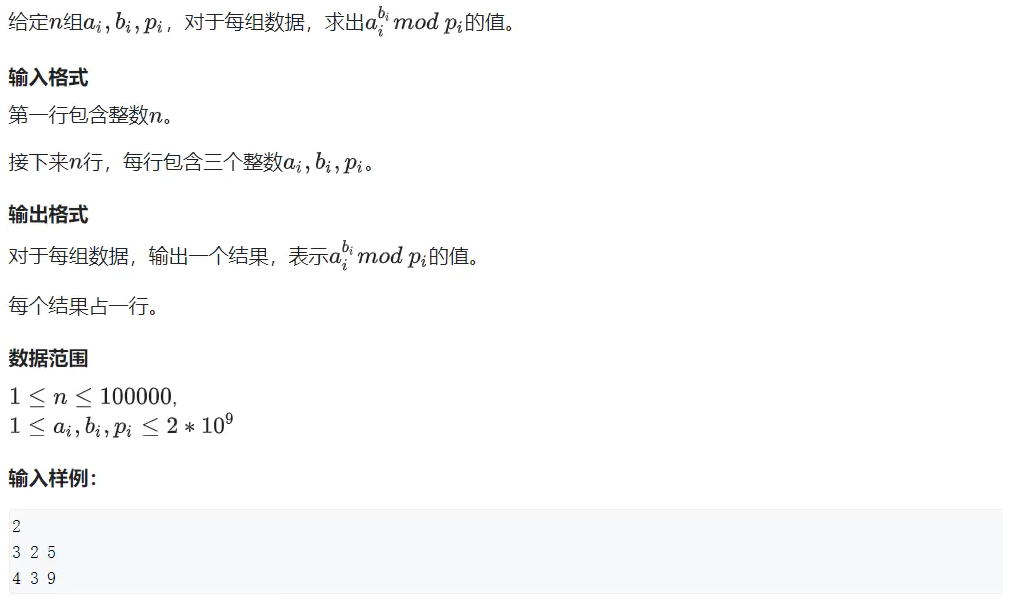
The time complexity can be O(log^k) Inside , Find out quickly a^k mod p Result , among a、p、k Can be in 10^9 Within the scope of

LeetCode+ 46 - 50_ Xiaoxuecai's blog -CSDN Blog

If you use violence, you need to cycle , loop k Time ,k be equal to 10^9, The time complexity is O(10^9)

If k = 10^9, The fast power can be O(log10^9) Calculate it within , That is, it only needs 30 Times operation

The core idea of fast power is the repeated square method , The following values need to be preprocessed , Range [ 0,logk ]

The time complexity of preprocessing is logk, Altogether logk Number

After preprocessing these values , How to handle a^k Combined ？

hold a^k It can be split into the form of the product of several numbers preprocessed in front , That is the k Split into the sum of the previous numbers , That is the k Just turn it into binary

k The binary representation of 、 The splittable results are as follows ,k All of the binary representations of are 1 Add the corresponding power to the bit of

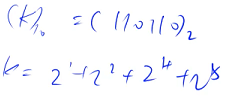
When calculating , Maximum disassembly logk Multiply the numbers , The time complexity of the whole algorithm is O(logk)

How to put this logk The number is preprocessed ？

Each number is the square of the above number mod p, Just square it from front to back k Time , You can put this logk The number preprocessing comes out . After pretreatment , Put... Directly a^k Divide it into the product of the previous numbers , It's just a way of k Split into 2 Add several powers of , Also is to see k Which bits in the binary representation of 1, Just put 1 Multiply the corresponding bits

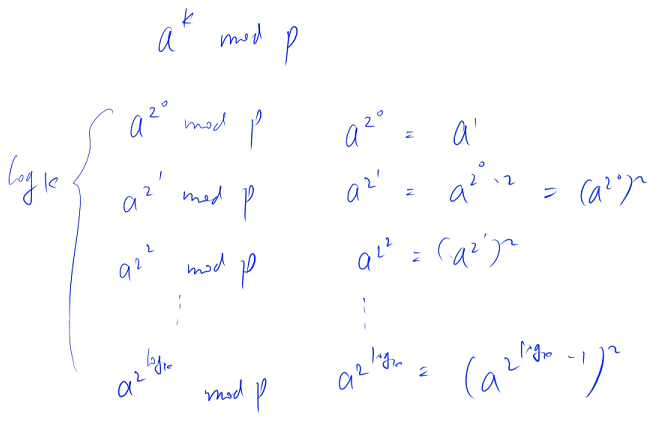
Here's an example , seek 4^5 mod 10 Result , Be careful p Not necessarily prime , First pretreatment , And then 4^5 Split

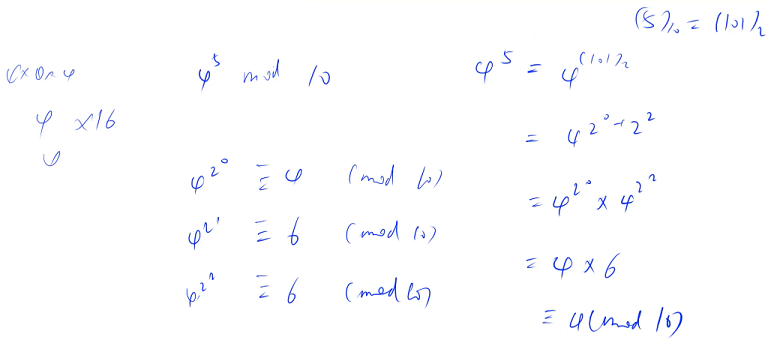
There are a lot of read data , Suggest using scanf Let's read it in

#include <iostream>
#include <algorithm>

using namesapce std;
// Because of the mold 10^9  And there is a product   Two 10^9 Multiplication may explode int Need to be written LL
typedef long long LL;

// return  a^k % p  Result 
int qmi(int a,int k,int p)
{
    // Define the answer 
    int res = 1;
    // seek  k  The binary representation of 
    // When  k!=0
    while(k)
    {
        /* 
            k & 1  Just look at  k  What is the number of digits , If at present  k  The last digit of is  1, Just multiply by  a^2^0
             Be careful  a  It's changing , Is constantly repeated square , At the beginning  a  Is the first item, that is  a^2^0, That is to say  a  own 
        */
        if(k & 1) res = (LL)res * a % p;
        /* 
             In each iteration, put  k  Delete the last digit of , Because the last digit has been calculated 
             see k The next bit of the binary representation of , The next one corresponds to  a  We should also put  a  Become the next 
        */
        k >>= 1;
        // hold  a^2^0  Become the next one, that is  a^2^1, That is the  a  square 
        a = (LL)a * a % p;
    }
    return res;
}

int main()
{
    int n;
    // altogether  n  Group data 
    scanf("%d", &n);
    // Each group  a,k,p
    while(n -- )
    {
        int a, k, p;
        scanf("%d%d%d", &a,&k, &p);
        // Go straight back to  a^k % p
        printf("%d\n", qmi(a, k, p));
    }
    return 0;
}

Fast power inverse

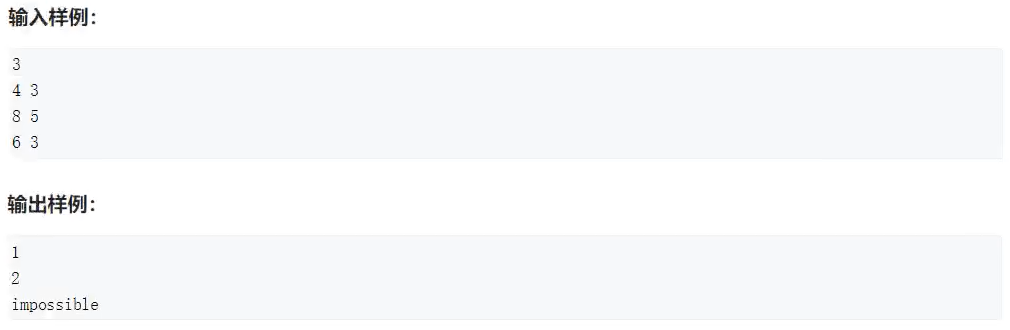
What is inverse element ？ The definition of multiplicative inverse is given below , If b and m Coprime , also b aliquot a Words , Then there is an integer x bring a / b congruence On a * x mod m, It's called x yes b model m Multiplicative inverse element of , Write it down as b^-1(mod m)

If a / b If it's a whole number , We hope not to do Division , Because division by remainder is a troublesome thing , We want to turn division into Multiplication , I hope to find a number that makes a / b The remainder of is congruence a * x(mod m), If for a b Can find one x, bring a / b and a * x(mod m) If the remainder is the same , Just put x called b model m Inverse element , Write it down as b^-1(mod m)

b The inverse of is a marker , No b^-1, It's an integer , We can divide everything by b The situation is converted to multiply b The inverse element of

It's better to turn division into Multiplication , Because division in number theory is not necessarily an integer , Multiply two integers or integers , Dividing two integers is not necessarily an integer

Properties of inverse elements

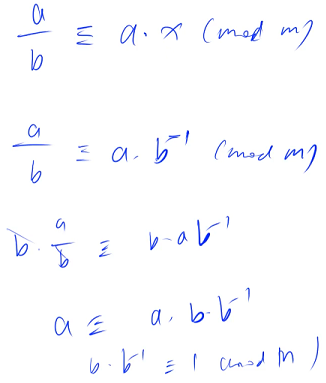
Definition of prime number

For all greater than 1 The natural number of ( from 2 The starting integer ) To define the ：2、3、4 . . . All less than or equal to 1 The integer of , It's neither prime nor sum

In more than 1 In the integer of , If only 1 And itself , It is called prime number , Prime or prime

The problem requires the inverse element , Give us one b, Ask to find one x, bring b * x ≡ 1 (mod p), A given p It must be prime , because p Prime number , From Fermat's small theorem , If b and p Coprime , There will be b^p-1 ≡ 1(mod p), Split one b,b * b^p-2 ≡ 1(mod p), If p Prime number , According to the properties of inverse element ,b The inverse of is b^p-2, in other words b^p-2 Namely b % p Inverse element , because p Prime number , therefore p Greater than or equal to 2, therefore p - 2 Greater than or equal to 0, It must be legal , So what this topic asks us is a^p-2 % p Result

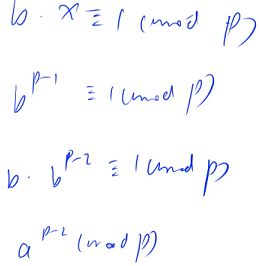
There is no solution , If b yes p There is no solution when it is a multiple of , If b and p There must be no solution for non coprime , because b yes p Multiple , that b * x It must be p Multiple ,mod p It must be more than 0, Impossible surplus 1, Only in this case is there no solution

If b No p Multiple , because p Prime number , therefore b and p It must be reciprocal , By Fermat theorem ,b^p - 1 A certain % p  more than 1, So there must be an inverse element , A set of solutions can be constructed from Fermat theorem

When p When it's a prime number, you can find it like this , If p If it is not a prime number, Fermat's theorem cannot be used , Fermat's theorem requires p It must be prime

#include <iostream>
#include <algorithm>

using namesapce std;
// Because of the mold 10^9  And there is a product   Two 10^9 Multiplication may explode int Need to be written LL
typedef long long LL;

// return  a^k % p  Result 
int qmi(int a,int k,int p)
{
    // Define the answer 
    int res = 1;
    // seek  k  The binary representation of 
    // When  k!=0
    while(k)
    {
        // At present k The last digit of is 1
        if(k & 1) res = (LL)res * a % p;
        // hold k Delete the last digit of 
        k >>= 1;
        // hold a square 
        a = (LL)a * a % p;
    }
    return res;
}

int main()
{
    int n;
    scanf("%d", &n);
    while(n -- )
    {
        // Enter a a and p  seek a^p-2%p
        int a, p;
        // use res Answer   Find out the answer first 
        int res = qmi(a, p - 2, p);
        scanf("%d%d", &a, &p);
        // If  a % p != 0, explain  a  No  p  Multiple , Put... Directly  res  Output is OK   Special judgement  2  Prime number  4 % 2  No coprime, no output 
        if(a % p) printf("%d\n", res);
        // Otherwise, there must be no solution  a  It must be  p  Multiple 
        else puts("impossible");
    }
    return 0;
}