当前位置:网站首页>L2-004 这是二叉搜索树吗? (25 分)
L2-004 这是二叉搜索树吗? (25 分)
2022-07-06 09:14:00 【%xiao Q】
题意:
要求你判断这是否是一颗二叉搜索树或其镜像按前序遍历的结果
分析:
我们可以先假设这个是二叉搜索树或其镜像按前序遍历的结果,然后在看是否符合下面的条件:
我们可以定义一个2个指针tl,tr,分别从前往后扫和从后往前的扫,tl从前往后找,找第一个比根节点节点大的位置(即右子树的第一个节点),tr从后往前找,找第一个比根节点小的位置(即右子树最后一个点),所以如果符合tl - tr == 1,那么就是符合题目要求的二叉树,关于这个原因,你们可以按样例来模拟一下。
参考代码:
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <cmath>
#include <queue>
#include <stack>
#include <algorithm>
#include <unordered_map>
#define LL long long
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define reps(i, a, b) for(int i = a; i < b; i++)
#define pre(i, a, b) for(int i = b; i >= a; i--)
using namespace std;
const int N = 1010;
int a[N];
vector<int> ans;
bool flag = true;
void dfs(int l, int r)
{
if(l > r) return ;
int tl = l + 1, tr = r;
// 判断是否符合二叉搜索树
if(flag)
{
while(tl <= r && a[tl] < a[l]) tl++; //找右子树的第一个
while(tr > l && a[tr] >= a[l]) tr--; //找做子树的最后一个
}
// 判断是否符合其镜像
else
{
while(tl <= r && a[tl] >= a[l]) tl++;
while(tr > l && a[tr] < a[l]) tr--;
}
if(tl - tr != 1) return ; //不符合条件,返回
dfs(l + 1, tr); //遍历左子树
dfs(tl, r); //遍历右子树
ans.push_back(a[l]); //按后续遍历来存
}
int main()
{
int n;
cin >> n;
rep(i, 1, n) cin >> a[i];
dfs(1, n);
if(ans.size() != n)
{
flag = false;
ans.clear();
dfs(1, n);
}
if(ans.size() != n) puts("NO");
else
{
puts("YES");
rep(i, 0, n - 1)
{
if(i) cout << " ";
cout << ans[i];
}
cout << endl;
}
return 0;
}
边栏推荐
- 软件测试与质量学习笔记3--白盒测试
- Installation and use of MySQL under MySQL 19 Linux
- Attention apply personal understanding to images
- Use dapr to shorten software development cycle and improve production efficiency
- In the era of DFI dividends, can TGP become a new benchmark for future DFI?
- 数据库高级学习笔记--SQL语句
- QT creator create button
- JDBC原理
- 打开浏览器的同时会在主页外同时打开芒果TV,抖音等网站
- AcWing 179. Factorial decomposition problem solution
猜你喜欢

One click extraction of tables in PDF
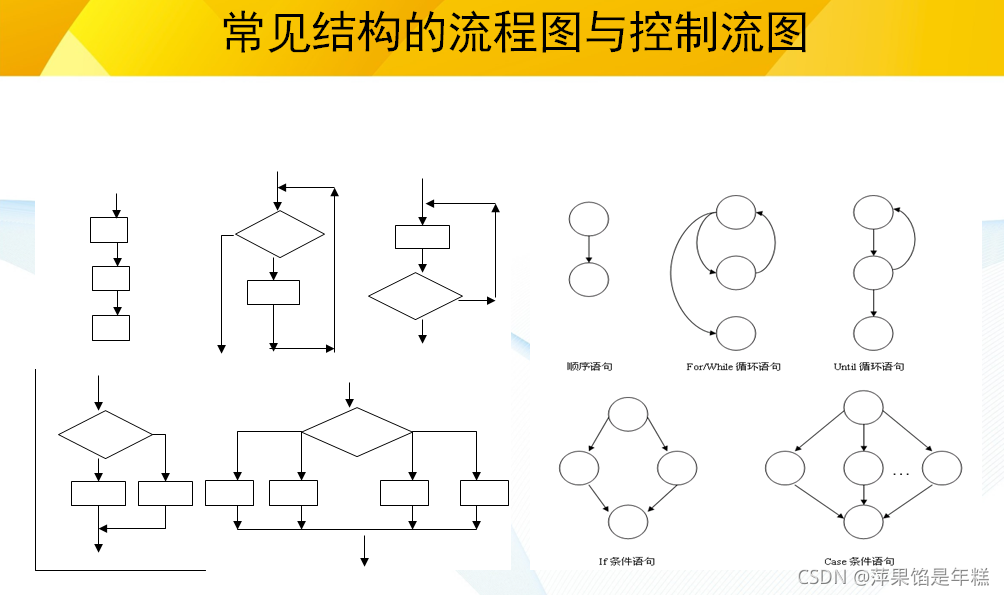
软件测试与质量学习笔记3--白盒测试
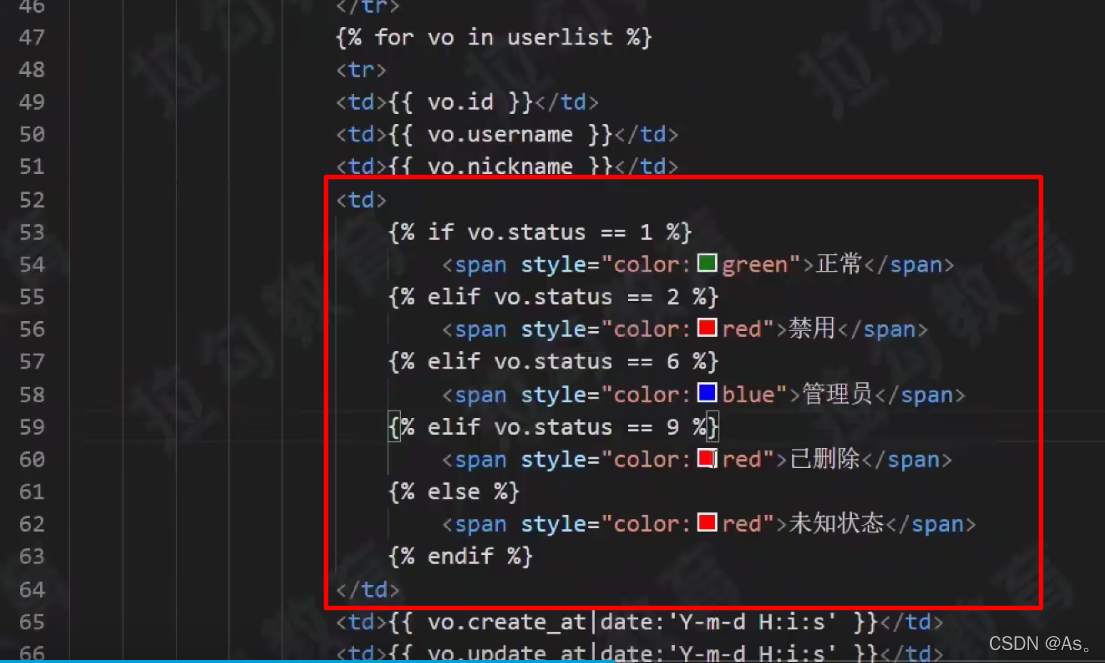
02 staff information management after the actual project
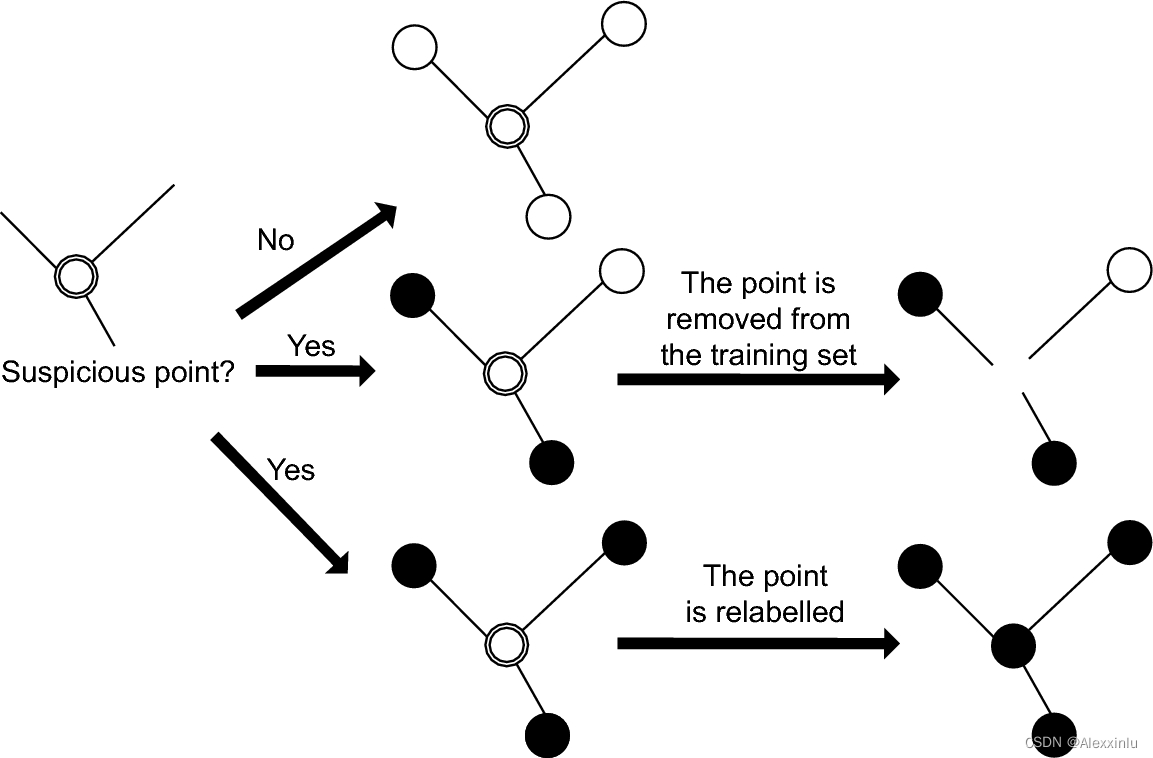
Csdn-nlp: difficulty level classification of blog posts based on skill tree and weak supervised learning (I)
![[number theory] divisor](/img/ec/036d7e76cc566c08d336444f2898e1.jpg)
[number theory] divisor
Pytorch基础
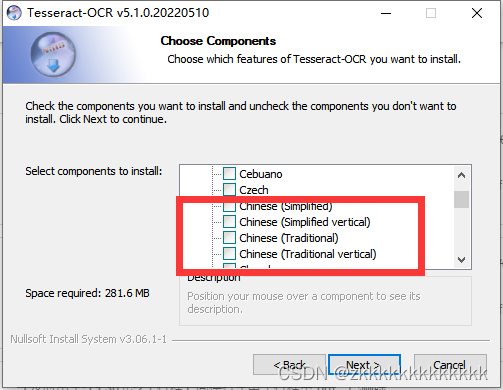
图像识别问题 — pytesseract.TesseractNotFoundError: tesseract is not installed or it‘s not in your path
![[Thesis Writing] how to write function description of jsp online examination system](/img/f8/13144e0febf4a576bbcc3290192079.jpg)
[Thesis Writing] how to write function description of jsp online examination system
引入了junit为什么还是用不了@Test注解
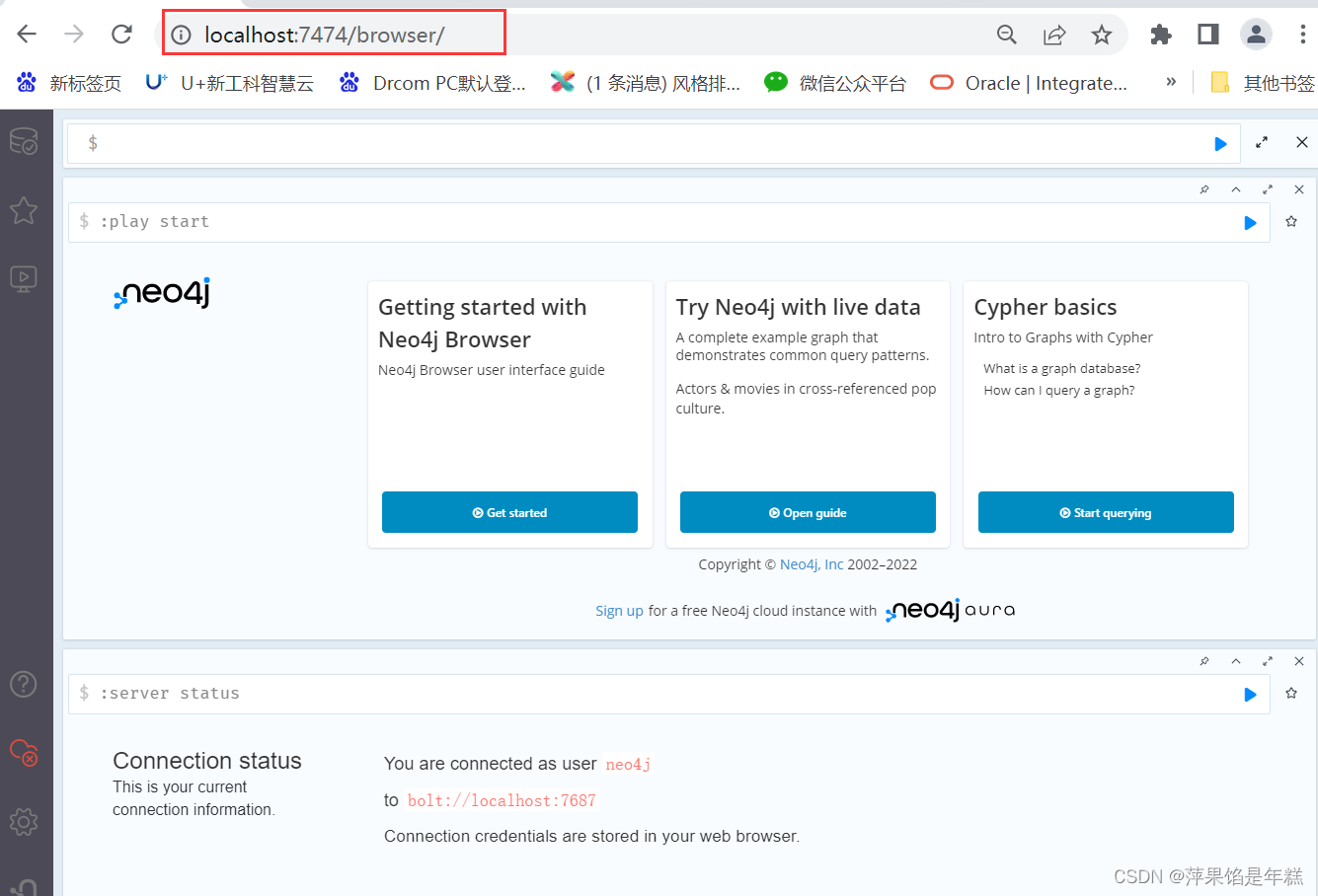
Neo4j installation tutorial
随机推荐
How to build a new project for keil5mdk (with super detailed drawings)
Leetcode 461 Hamming distance
Postman environment variable settings
Installation and use of MySQL under MySQL 19 Linux
AcWing 1294. Cherry Blossom explanation
02-项目实战之后台员工信息管理
Basic use of redis
SSM integrated notes easy to understand version
Install MySQL for Ubuntu 20.04
Navicat 導出錶生成PDM文件
【博主推荐】SSM框架的后台管理系统(附源码)
【博主推荐】asp.net WebService 后台数据API JSON(附源码)
The virtual machine Ping is connected to the host, and the host Ping is not connected to the virtual machine
Classes in C #
[download app for free]ineukernel OCR image data recognition and acquisition principle and product application
Windows cannot start the MySQL service (located on the local computer) error 1067 the process terminated unexpectedly
[free setup] asp Net online course selection system design and Implementation (source code +lunwen)
Install mongdb tutorial and redis tutorial under Windows
Why can't I use the @test annotation after introducing JUnit
Julia 1.6 1.7 common problem solving