当前位置:网站首页>The longest ascending subsequence model acwing 482 Chorus formation
The longest ascending subsequence model acwing 482 Chorus formation
2022-07-07 14:13:00 【T_ Y_ F666】
Longest ascending subsequence model AcWing 482. Chorus formation
Original link
Algorithm tags
DP linear DP Longest ascending subsequence
Ideas
Ask for i Ending ascending sequence , With i The reverse rising at the end is the descending sequence , Get to i It is a sequence in which the dividing point rises first and then falls , Taking the maximum , Reduce the total by the maximum .
Code
#include<bits/stdc++.h>
#define int long long
#define rep(i, a, b) for(int i=a;i<b;++i)
#define Rep(i, a, b) for(int i=a;i>=b;--i)
using namespace std;
const int N = 1005, INF = 0x3f3f3f3f;
int f[N], f1[N], a[N];
inline int read(){
int s=0,w=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
return s*w;
}
void put(int x) {
if(x<0) putchar('-'),x=-x;
if(x>=10) put(x/10);
putchar(x%10^48);
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n=read();
rep(i, 1, n+1){
a[i]=read();
}
int ans=0, ans1=0, ans2=0;
// With i Ending ascending sequence
rep(i, 1, n+1){
f[i]=1;
rep(j, 1, i){
if(a[j]<a[i]){
f[i]=max(f[i], f[j]+1);
}
}
ans1=max(ans1, f[i]);
}
// With i The reverse rising at the end is the descending sequence
Rep(i, n, 0){
f1[i]=1;
Rep(j, n, i+1){
if(a[j]<a[i]){
f1[i]=max(f1[i], f1[j]+1);
}
}
ans2=max(ans2, f1[i]);
}
// Go up first Post descent sequence
rep(i, 1, n+1){
ans=max(ans, (f[i]+f1[i]-1));
}
printf("%lld\n", n-ans);
}
And y The general code is consistent
y Master code
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n;
int h[N];
int f[N], g[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &h[i]);
for (int i = 0; i < n; i ++ )
{
f[i] = 1;
for (int j = 0; j < i; j ++ )
if (h[i] > h[j])
f[i] = max(f[i], f[j] + 1);
}
for (int i = n - 1; i >= 0; i -- )
{
g[i] = 1;
for (int j = n - 1; j > i; j -- )
if (h[i] > h[j])
g[i] = max(g[i], g[j] + 1);
}
int res = 0;
for (int i = 0; i < n; i ++ ) res = max(res, f[i] + g[i] - 1);
printf("%d\n", n - res);
return 0;
}
Originality is not easy.
Reprint please indicate the source
If it helps you Don't forget to praise and support 
边栏推荐
猜你喜欢
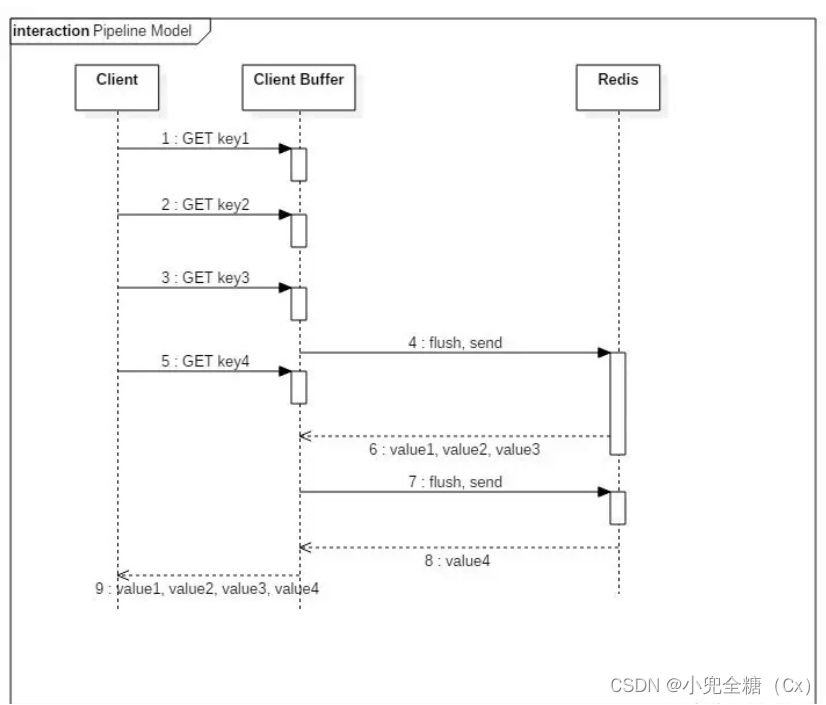
. Net core about redis pipeline and transactions

TPG x AIDU | AI leading talent recruitment plan in progress!
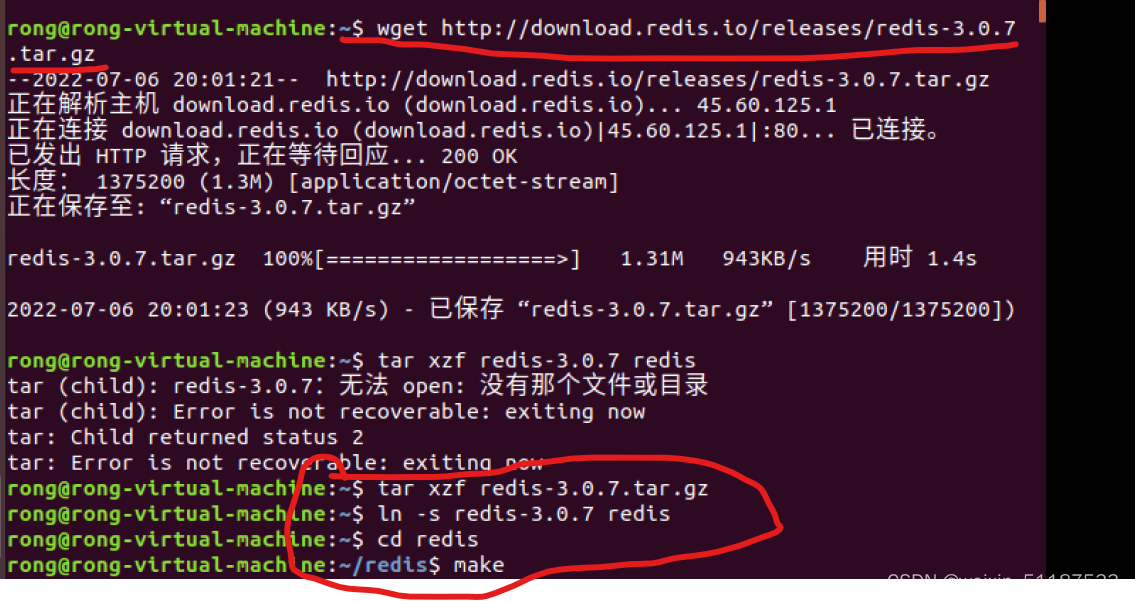
2022-7-6 beginner redis (I) download, install and run redis under Linux
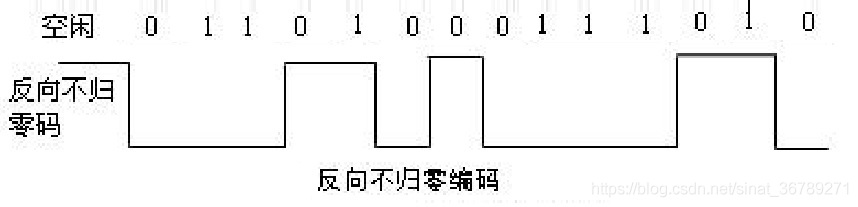
常用数字信号编码之反向不归零码码、曼彻斯特编码、差分曼彻斯特编码

Advanced Mathematics - Chapter 8 differential calculus of multivariate functions 1

最长上升子序列模型 AcWing 482. 合唱队形

最长上升子序列模型 AcWing 1012. 友好城市

UML 状态图
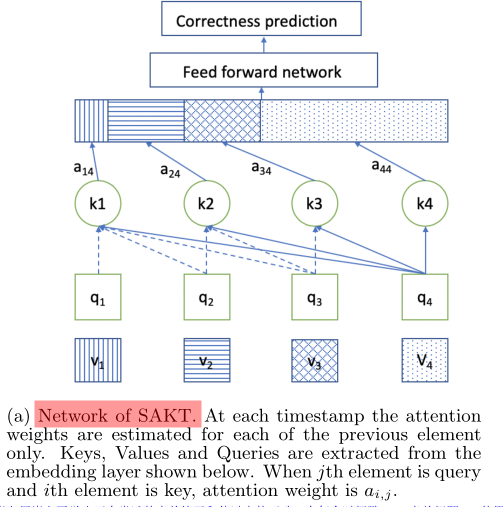
Introduction to sakt method

高等数学---第八章多元函数微分学1
随机推荐
Hands on Teaching: XML modeling
IP address home location query full version
ES日志报错赏析-Limit of total fields
Horizontal of libsgm_ path_ Interpretation of aggregation program
2022-7-6 sigurg is used to receive external data. I don't know why it can't be printed out
2022-7-6 Leetcode 977. Square of ordered array
566. 重塑矩阵
Realization of search box effect [daily question]
The delivery efficiency is increased by 52 times, and the operation efficiency is increased by 10 times. See the compilation of practical cases of financial cloud native technology (with download)
供应链供需预估-[时间序列]
Redis 核心数据结构 & Redis 6 新特性详
Best practice | using Tencent cloud AI willingness to audit as the escort of telephone compliance
gvim【三】【_vimrc配置】
2022-7-6 Leetcode27. Remove the element - I haven't done the problem for a long time. It's such an embarrassing day for double pointers
How to check the ram and ROM usage of MCU through Keil
UML sequence diagram (sequence diagram)
高等數學---第八章多元函數微分學1
PostgreSQL array type, each splice
566. Reshaping the matrix
Excuse me, I have three partitions in Kafka, and the flinksql task has written the join operation. How can I give the join operation alone