当前位置:网站首页>Lee‘s way of Deep Learning 深度学习笔记
Lee‘s way of Deep Learning 深度学习笔记
2022-08-04 05:29:00 【视觉菜鸟Leonardo】
跟随吴恩达教授的深度学习课程,在这记录笔记。
B站视频:[双语字幕]吴恩达深度学习deeplearning.ai_哔哩哔哩_bilibili
一、神经网络
1.什么是神经元:
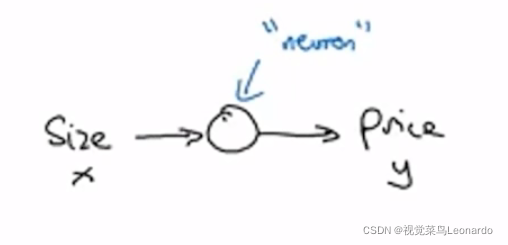
中间圆圈代表神经元,在这个神经元中可以完成从size到price的变化,也就是说神经元起到一个函数作用。

神经元中经常出现这个函数,称为“Relu函数”,意为“修正”,舍去所有负值,将其变为0。
往往影响输出y的因素有很多个,由不同的神经元组成:
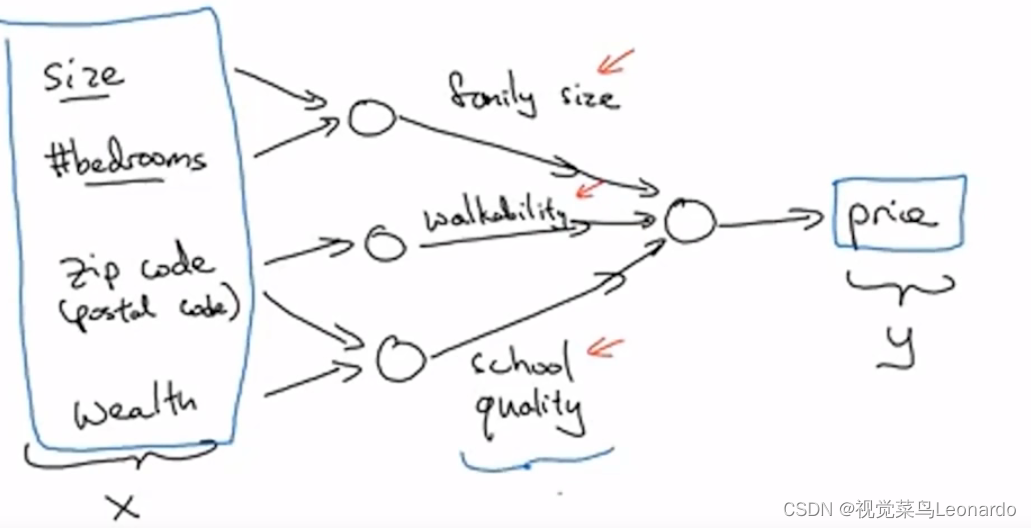
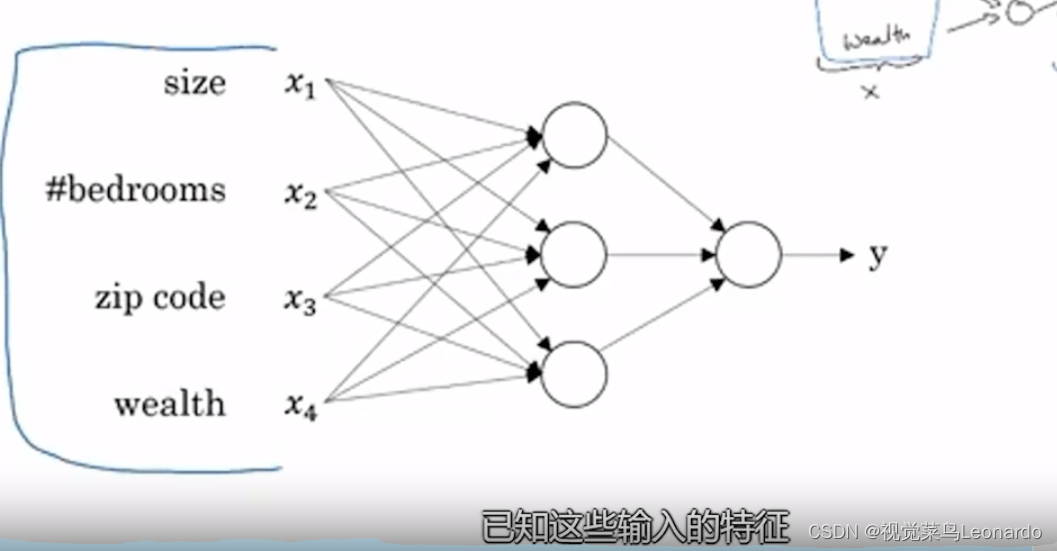
二、监督学习
现阶段的神经网络基本上都是以监督学习为基础
三、Deep Learning
深度学习基于机器学习,神经网络训练样本越多,结果越准确、
sigmoid函数:
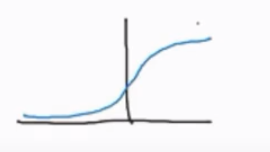
对于使用“梯度下降法”,当激活函数为sigmoid时,在最左侧和最右侧梯度几乎为零,速度很慢;Relu函数左侧梯度为零,右侧梯度恒为1,速度快,但增加计算。
四、二分类
logistic回归是一个用与二分分类的算法。
对于一个64x64大小的图片,则有大小为64x64x3的特征向量X。
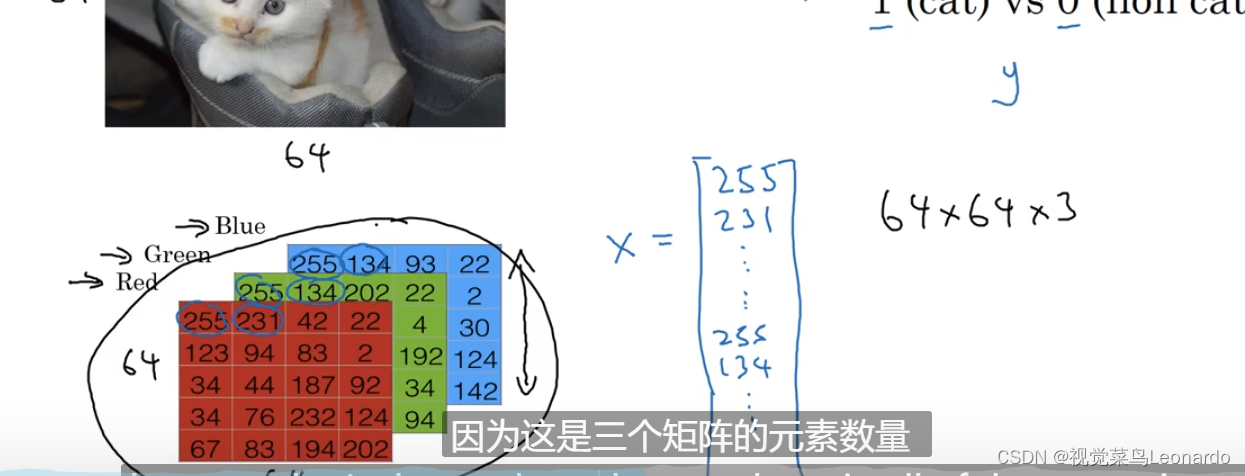
n可以代表维度,此图中有64x64x3=12288维。
在二分类问题中,目标是训练出一个分类器,以x为输入,预测结果y为输出(1、0)
x->y

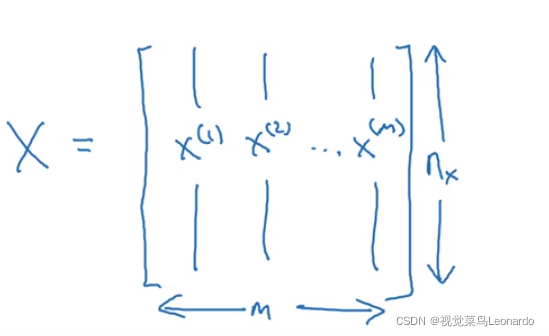
m为样本数,nx为矩阵高度

五、logistic回归
一般来说输入为x,输出为y,我们往往用一个y^来代表y=1时的概率,因为是线性函数,有y^=Wx+b,但是这样的输出y^往往不是0-1之间,就不代表概率,所以我们使用sigmoid激活韩式,来规范区间:
y^=sigmoid(Wx+b)
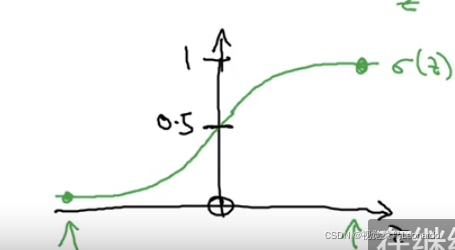 横轴为z
横轴为z
sigmoid(z)=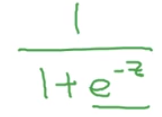
由图中我们就会得到一个概率
若要知道w和b,需要定义一个成本函数(cost function)
六、logistic回归损失函数
损失函数(lost function):用来定义y^和y的实际值到底有多接近
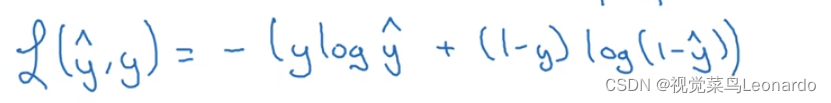
两种情况,想要y=1时,根据损失函数计算,需要让y^越大;
y=0时,需要让y^越小。
损失函数代表的是单个样本的标新情况,而成本函数J代表的是全体样本。
成本函数(cost function)

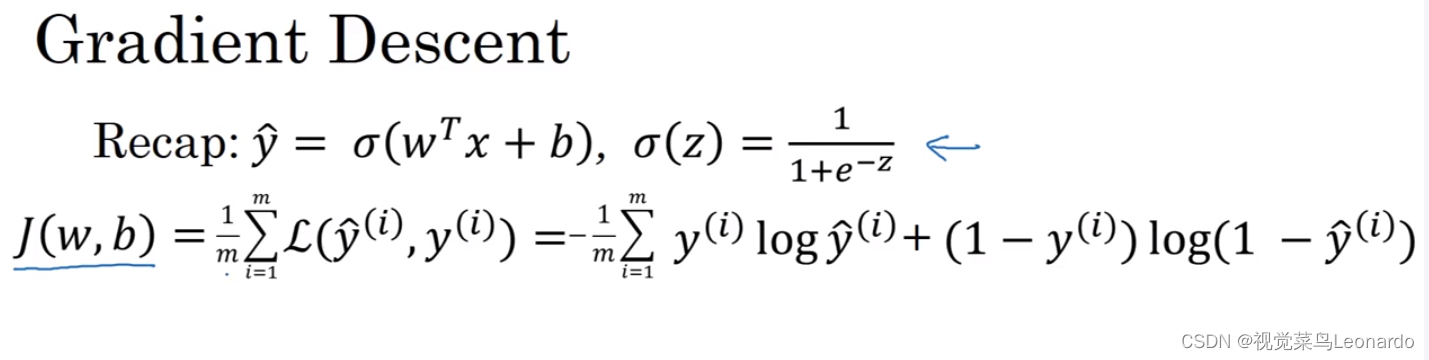
logistic回归可被看做一个很小的神经网络
七、梯度下降法
使用梯度下降法来训练或学习训练集上的参数w和b

八、计算图

九、m个样本的梯度下降
成本函数J
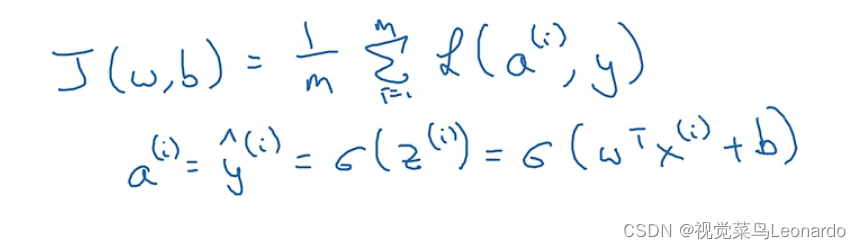
此时对全部样本进行求解导数时,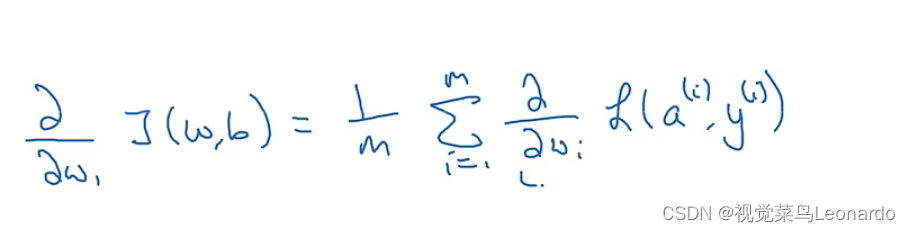
代码实现logistic回归:

理解:(1)上标i代表每一个训练样本,成本函数J代表的是全局均值
(2)dz其实就是代表的函数z的变化率,x*dz表示在这期间w变化成了多少
(3)每一个样本都都相应的变化率,最终结果为求和取平均
(4)w代表影响预测结果的特征,需要使用for循环来完成wi的计算
单纯的使用for循环会使得运算量极大且运行速度慢,于是便有向量化来解决这个问题。
十、向量化
传统方法使用wi*xi来计算再累加,太慢
向量化:z=np.dot(w,x)+b(矩阵乘法)
十一、神经网络
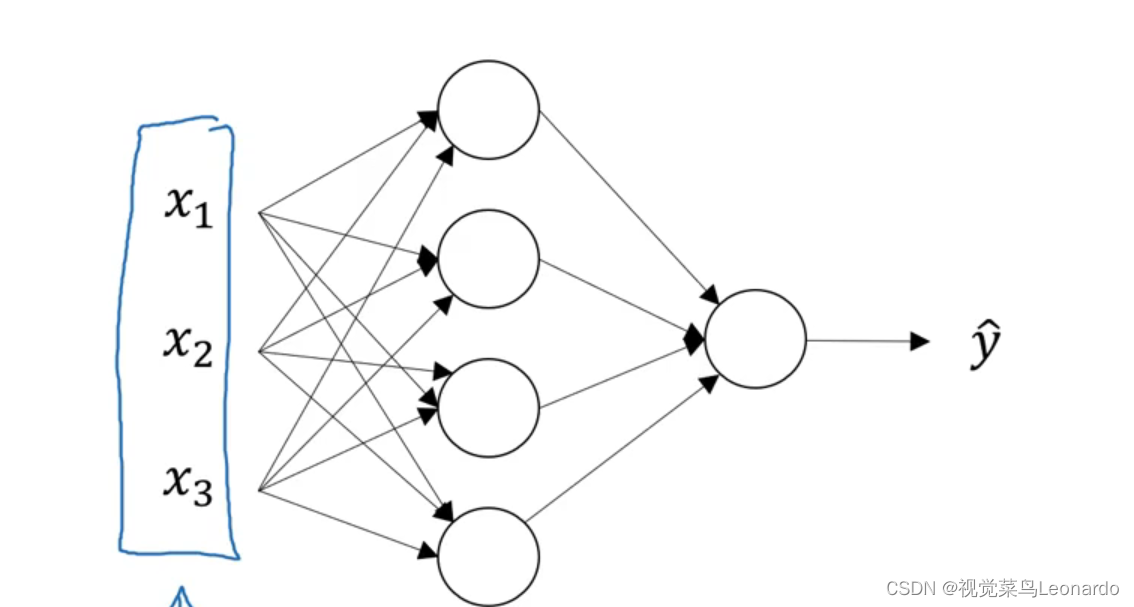
从左往右:输入层、神经网络隐藏层、输出层
向量x表示输入特征,也可以用a[0]表示,a也有激活的意思
隐藏层用a[1]表示
输出层用a[2]表示,最后y^=a[2]
以上双层神经网络(单隐层神经网络),不算输入层
隐藏层的节点涵盖了logistic回归的操作
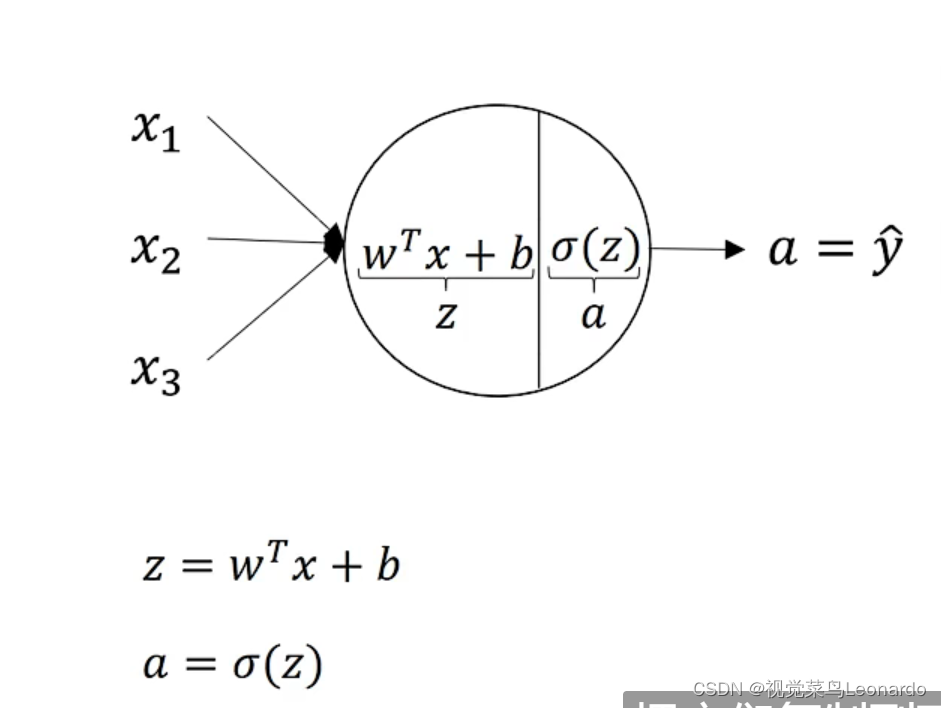
依次计算隐藏层的每一个节点:

在实际计算中,需要得到每一个z值,使用向量化计算更直接:
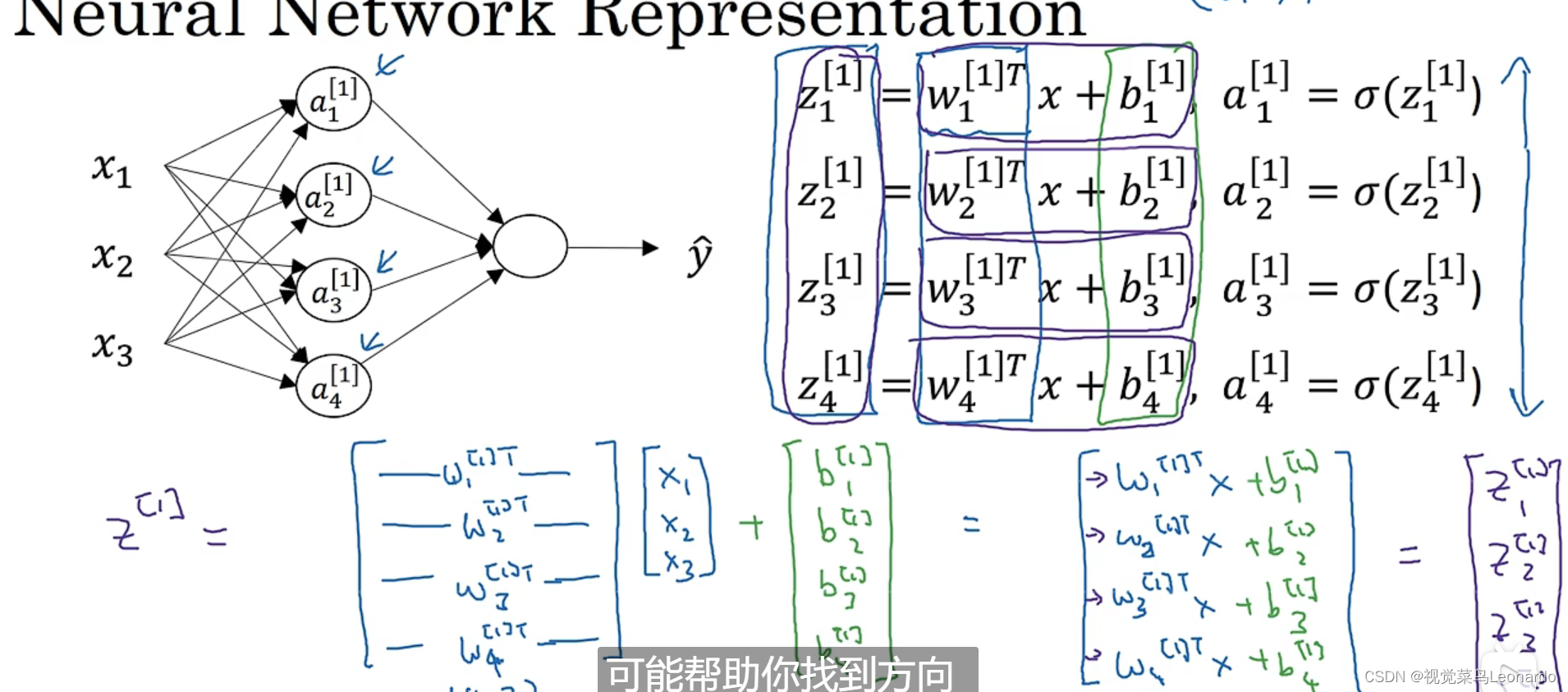
在多样本神经网络中,a[2](2) [2]代表第二层,(2)代表第二个样本
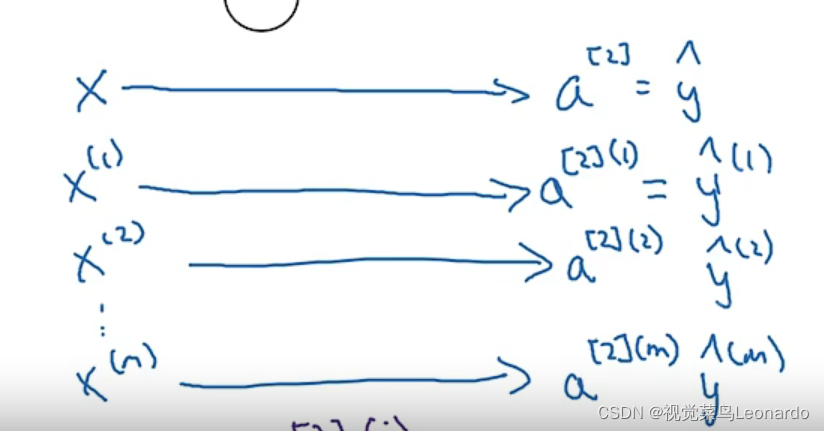
十二、计算机视觉
1.卷积
6x6的矩阵与3x3的filter进行卷积得到4x4的矩阵
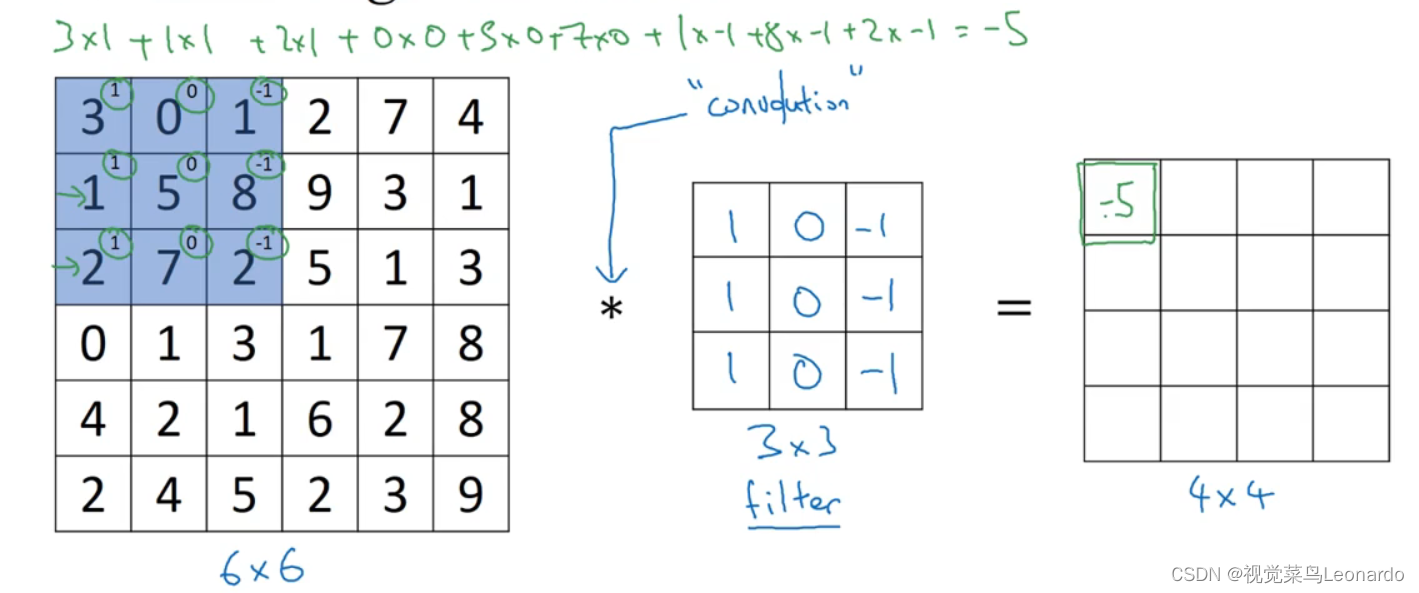
-5=3x1+0x0+1x-1+1x1+5x0+8x-1+2x1+7x0+2x-1
同理得到其他数值
边缘检测示例: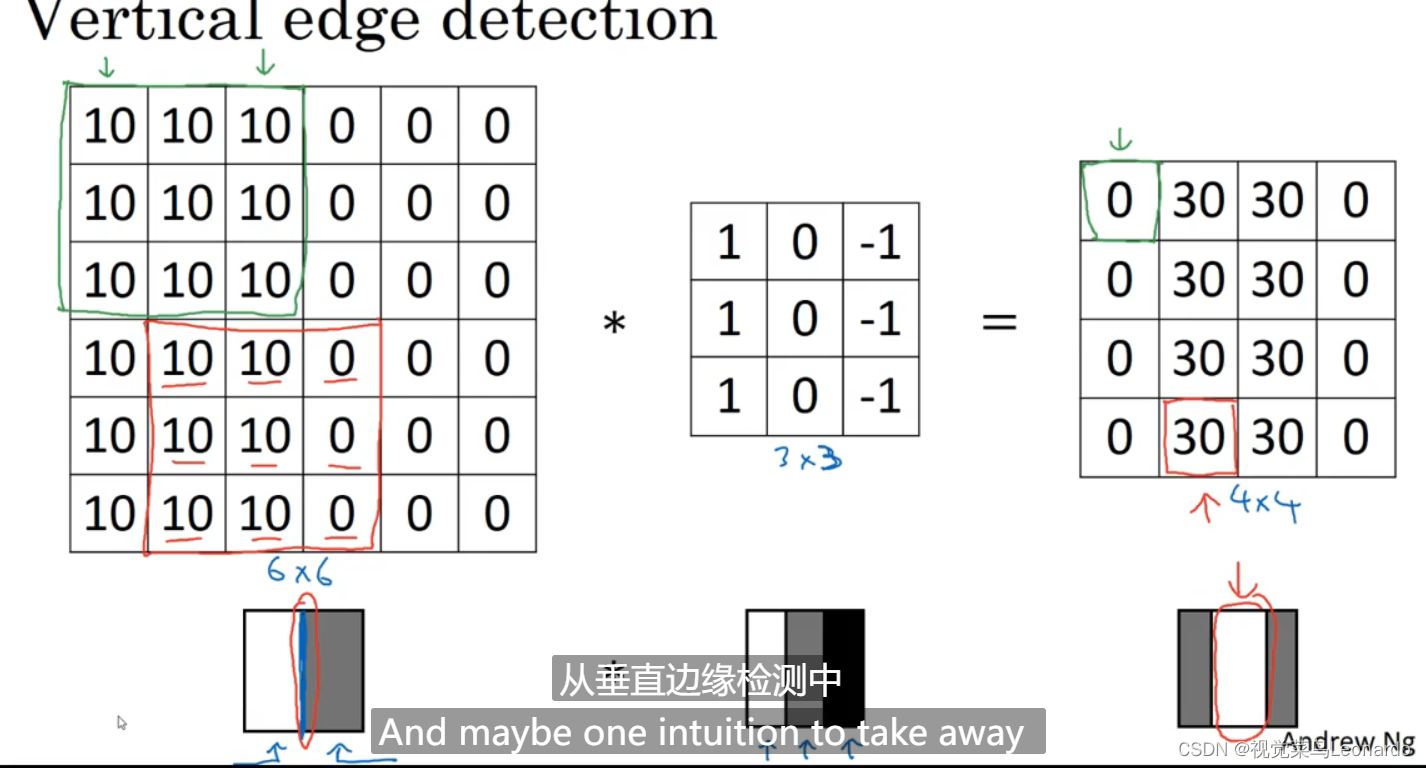
边缘处有明显的灰度值过渡,经过卷积核卷积后,便能得到边缘轮廓
2.padding
正常的卷积过后得到的图像都要比先前的小,如果有深层网络,那么最后会得到一个很小的图像,为了解决这个问题,在矩阵外围套上一圈0,最后得到的图像大小不变
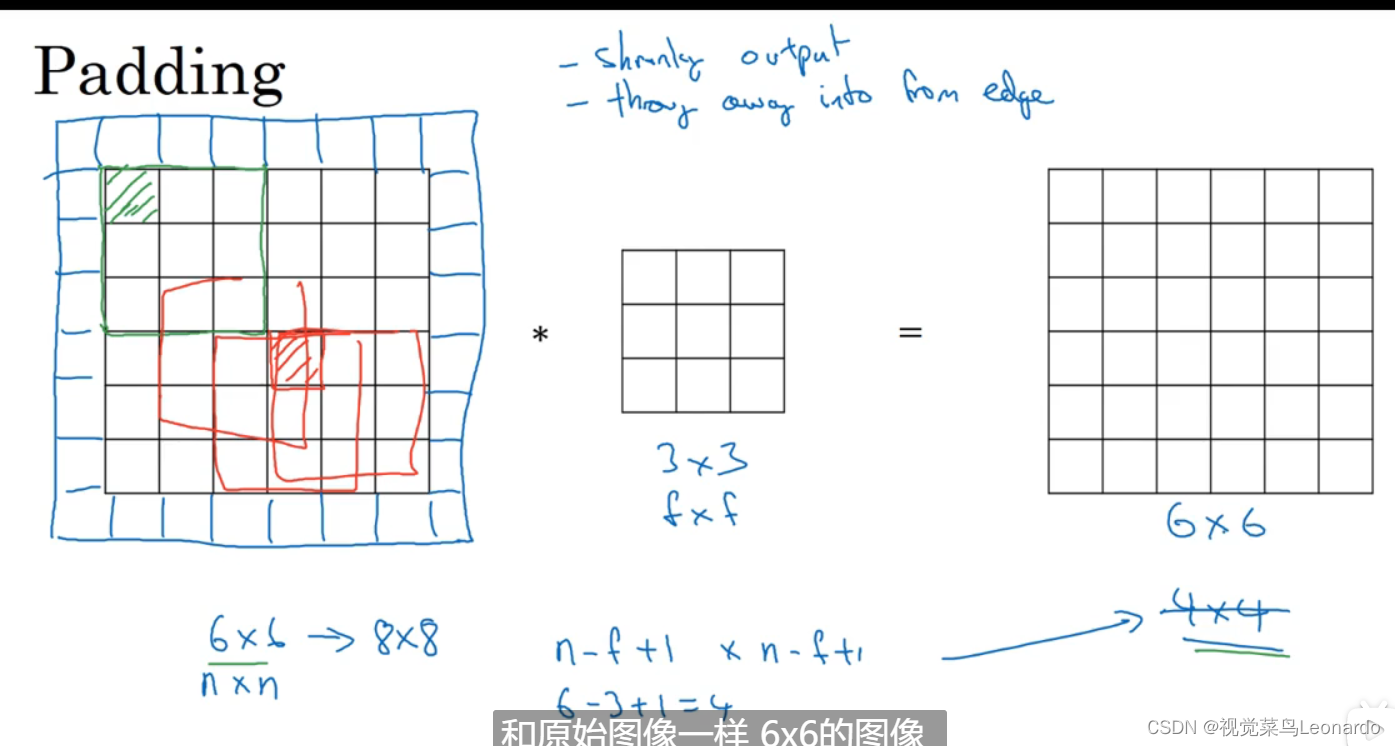
Valid 与 Same卷积
Valid代表不扩充,最后得到(n-f+1)*(n-f+1)大小的矩阵;
Same代表扩充,最后大小不变
3.步长Stride
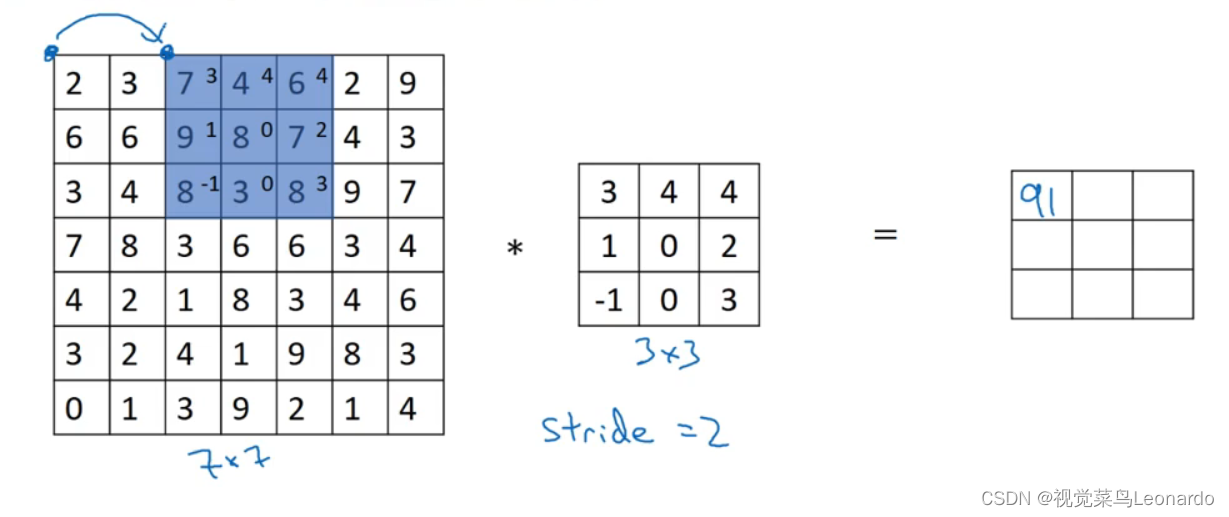
卷积核向右、向下移动的距离
nxn * fxf 步长为s 最后得到 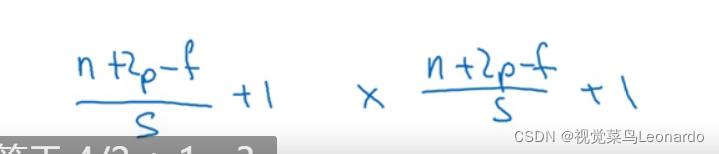
此符号代表向下取整: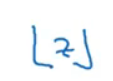

4.三维卷积
对于RGB图像有三个通道,其对应的卷积核也应该有三通道,二者卷积生成一张通道为1的图像
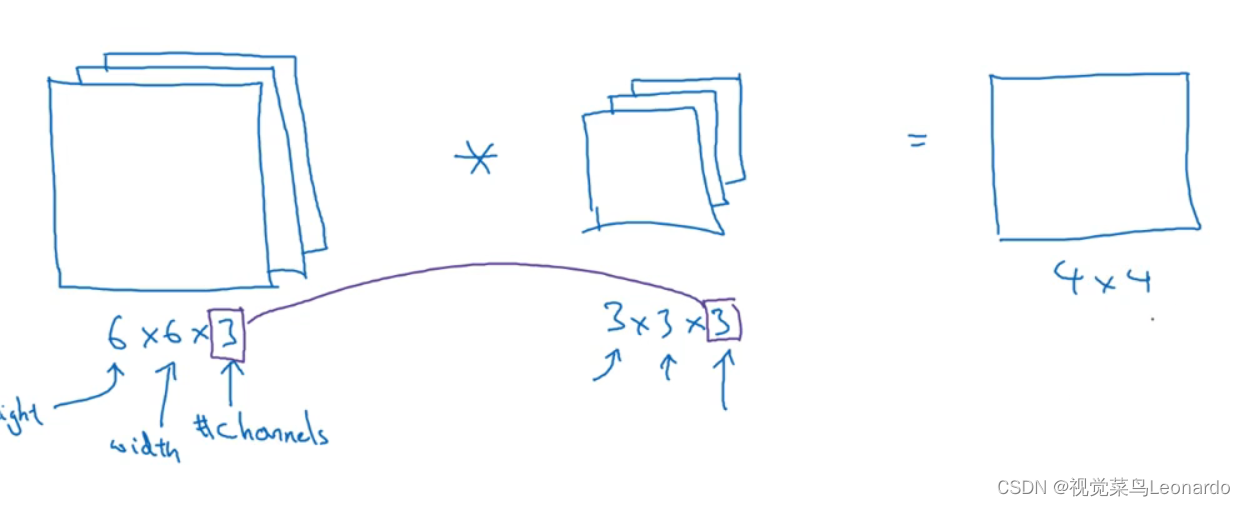
道理与灰度图像卷积相同,只不过是三通道最后得到的数是27个相乘结果相加
使用一个滤波器最终输出只能有垂直检测的图像,若要同时显示水平检测,需要再加上一个滤波器,最终输出两层叠加到一起的图像。
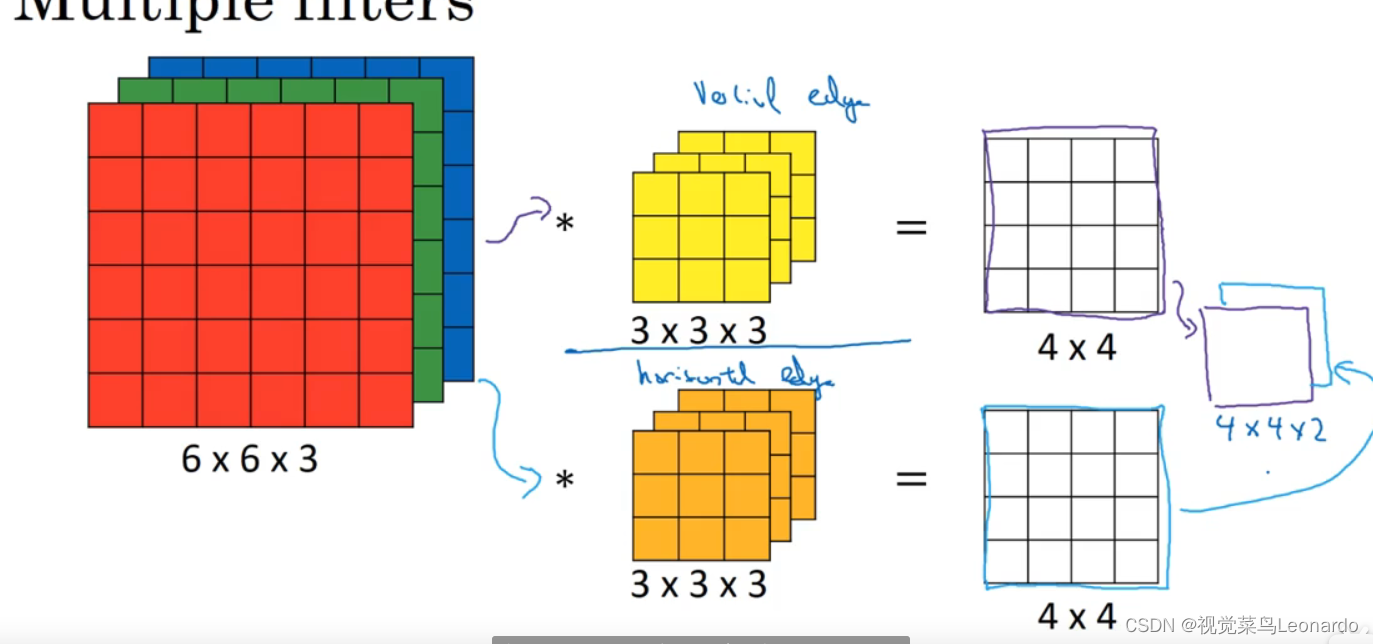
十三、卷积网络
1.单层卷积网络
卷积层的各种标记:
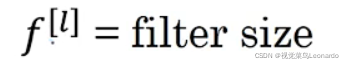 第l层过滤器大小 fxf
第l层过滤器大小 fxf
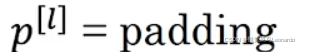 第l层padding的数量
第l层padding的数量
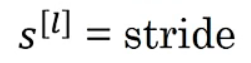 第l层步长大小
第l层步长大小
输入Input: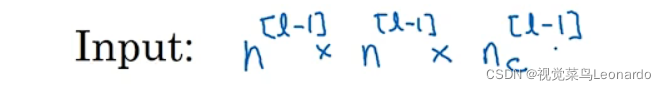
上一层的n和通道数nc
输出Output:
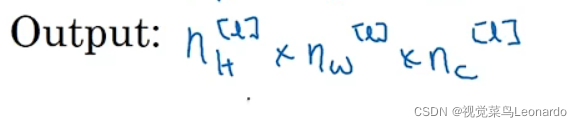
输出大小: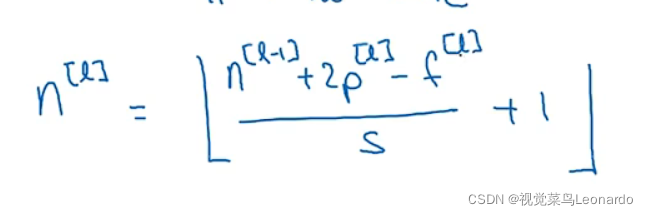
过滤器数量nc:
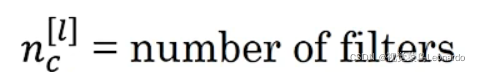
过滤器数量必须与输入图像的通道数相同,即与上一个图像输出的通道数相同
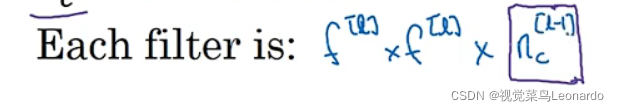
一个激活值: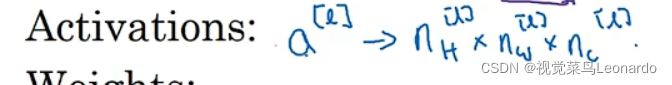
m个样本:
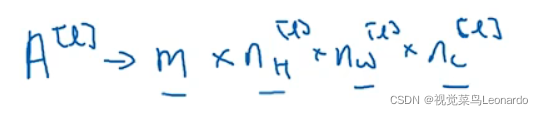
bias:(1,1,1,nc[l])
2.简单的卷积网络
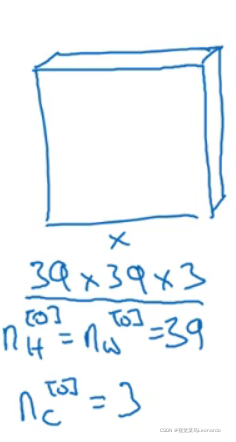
三通道,大小为39x39,
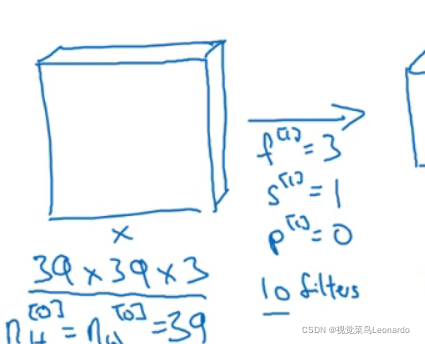
滤波器为3x3,步长为1,padding为0,10个滤波器。得到:

大小为37x37,通道数为10,再进行卷积:.
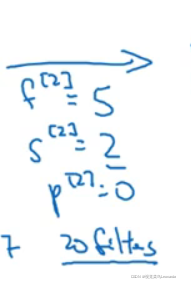
………………………………
最后得到:

在进行平滑处理得到1960个单元进行logistic回归/softamx,判断是否有猫:

卷积网络的趋势:图片面积在不断减小,通道数在不断增加,卷积其实就是特征提取器
卷积网络通常有三层:卷积层(conv)、池化层(Pool)、全连接层(FC)
3.池化层(Pooling)
使用池化层来缩减模型大小,提高训练速度,提高鲁棒性
看起来像使用了一个2x2的过滤器,步长为2,得到了后面的图像
最大池化(Max pooling):选取该区域最大值,前后通道数不变
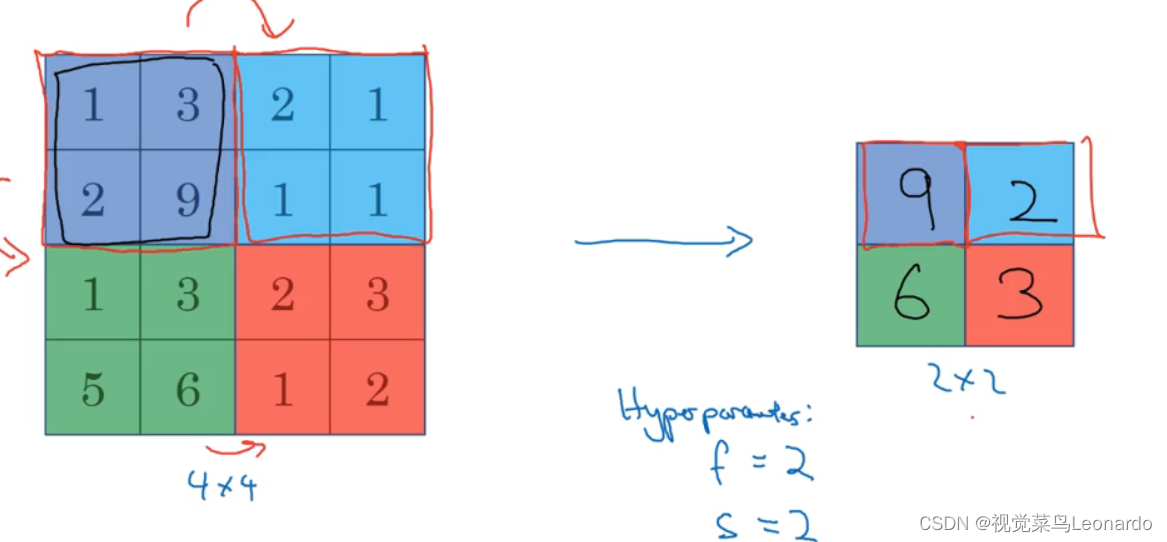
平均池化(Average pooling):选取该区域平均值,前后通道数不变
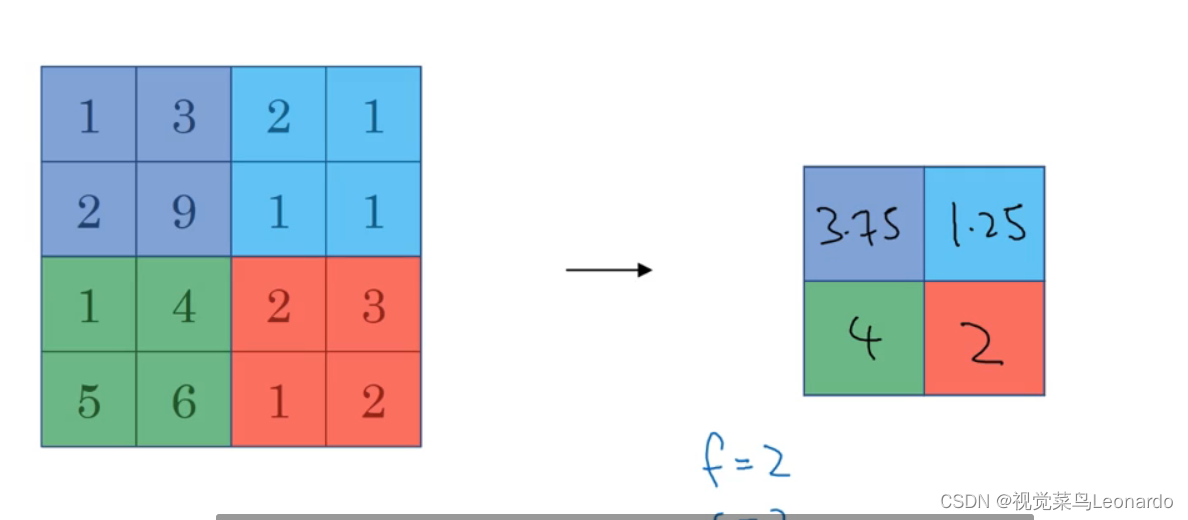
池化的超级参数Hyperparameters:
f:过滤器大小;
s:步长
最大池化或平均池化
4.卷积神经网络
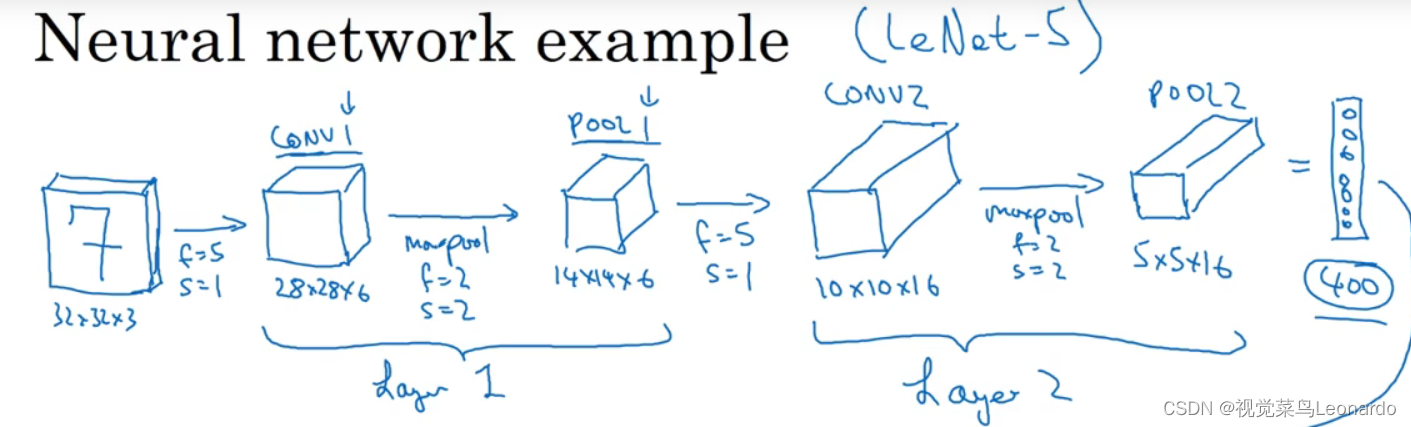
卷积层和池化层为同一层, 经过两层网络后变成400个元素的单排列,后接上全连接层,全连接层的概念与单神经网络类似
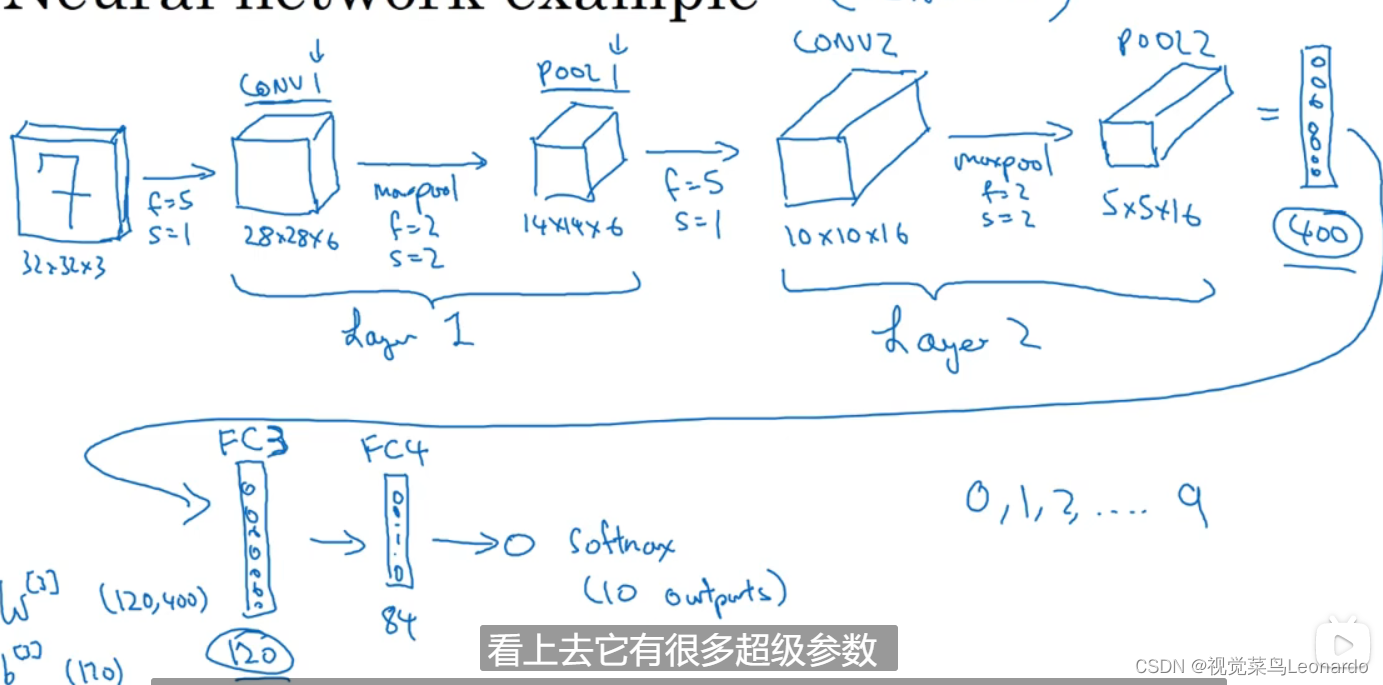
最后接上softmax,包含10各元素(0,1,2,……,9 )
十四、经典网络
1.LeNet-5
使用LeNet-5网络来识别手写数字,针对灰度图像,只有单通道
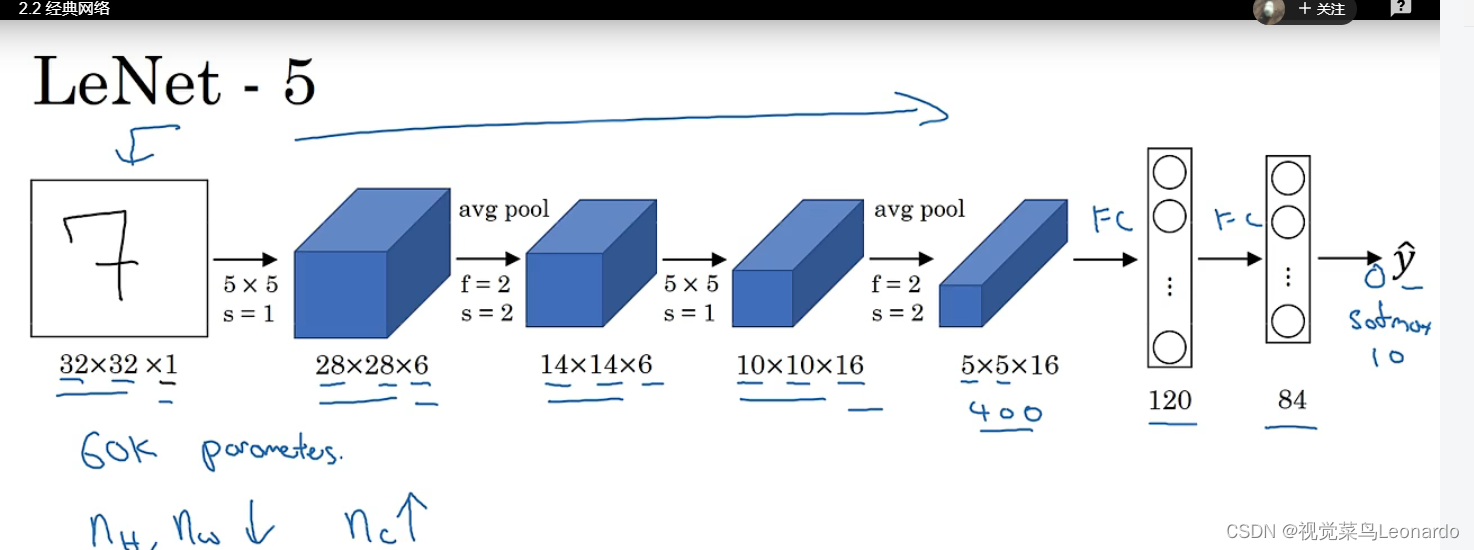
2.AlexNet
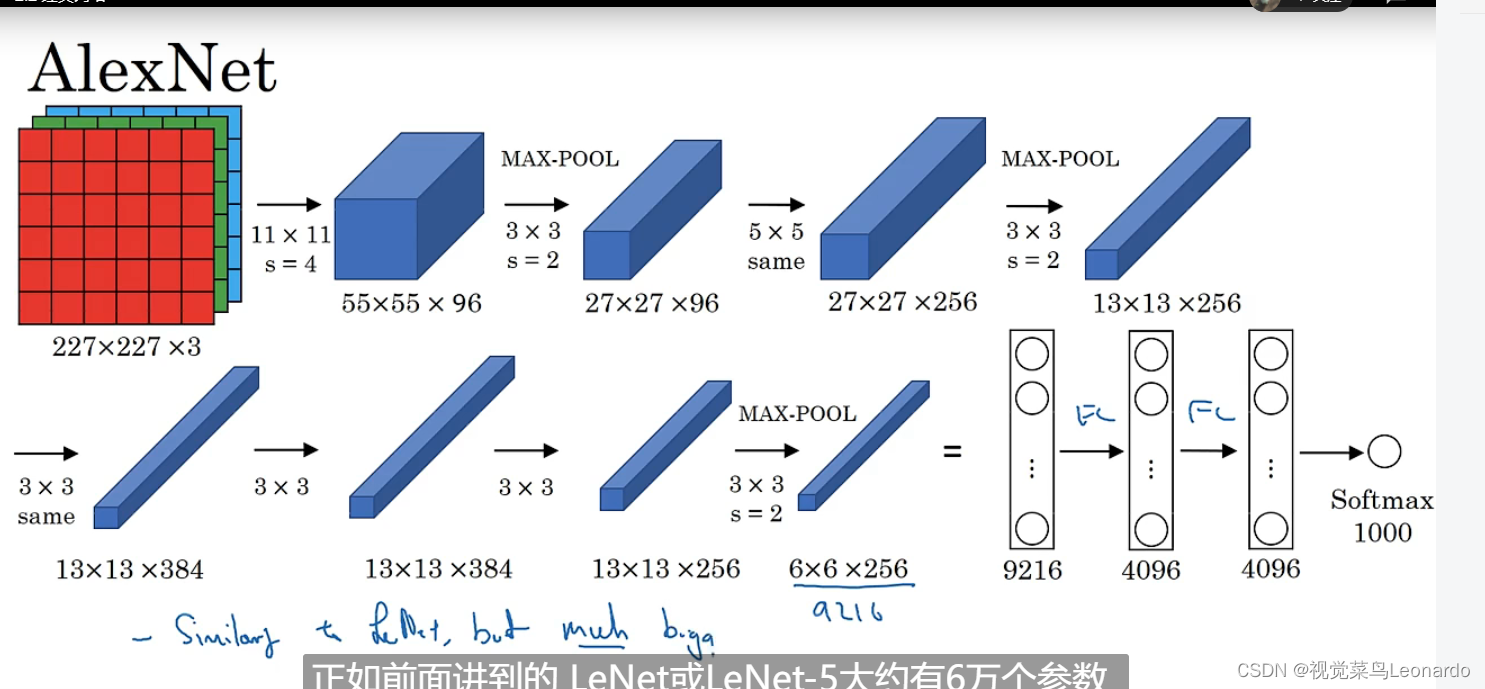
3.VGG-16
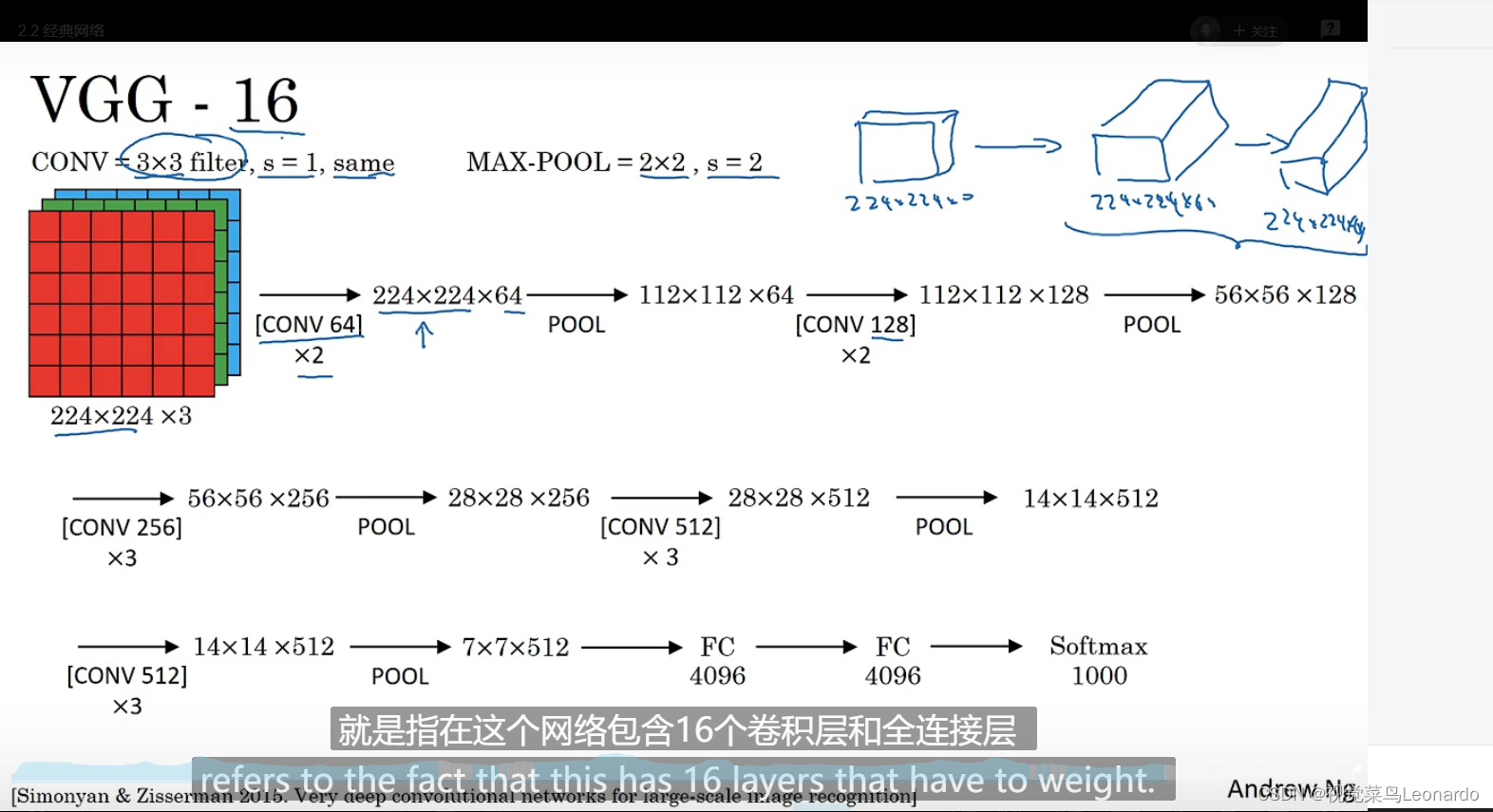
十五、激活函数
tanh函数:a=tanh(z)=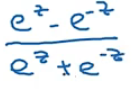
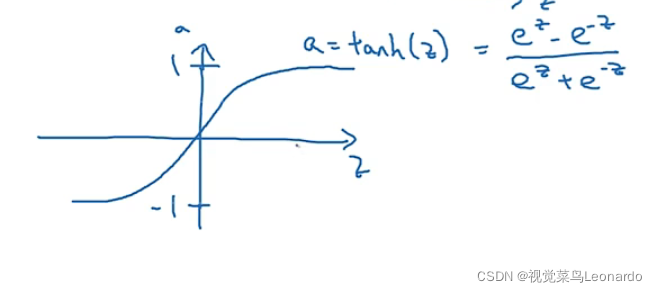
tanh函数比sigmoid函数更出色,除了二分类任务在输出层输出0,1.
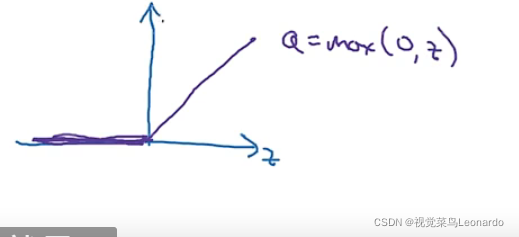
如果z很大或很小时,斜率更容易为0,此时使用Relu函数(修正线性单元)更合适
a=max(0,z)
边栏推荐
- MySQL最左前缀原则【我看懂了hh】
- 【CV-Learning】图像分类
- WARNING: sql version 9.2, server version 11.0. Some psql features might not work.
- Image-Adaptive YOLO for Object Detection in Adverse Weather Conditions
- npm install dependency error npm ERR! code ENOTFOUNDnpm ERR! syscall getaddrinfonpm ERR! errno ENOTFOUND
- 多项式回归(PolynomialFeatures)
- TensorFlow2学习笔记:6、过拟合和欠拟合,及其缓解方案
- IvNWJVPMLt
- 图像线性融合
- MAE 论文《Masked Autoencoders Are Scalable Vision Learners》
猜你喜欢
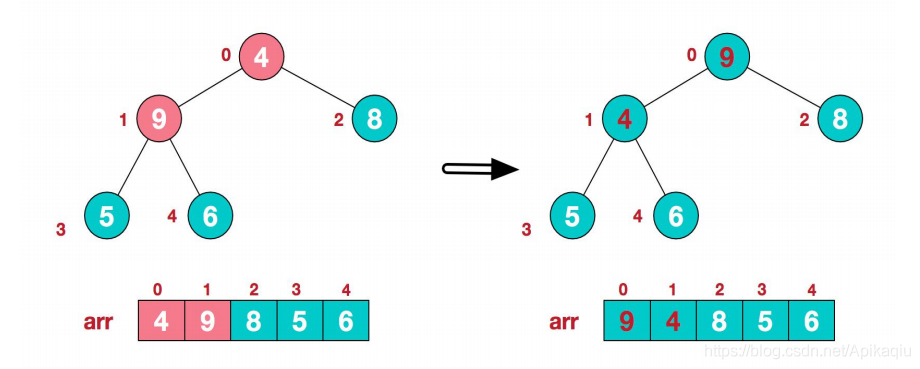
(十一)树--堆排序
npm install dependency error npm ERR! code ENOTFOUNDnpm ERR! syscall getaddrinfonpm ERR! errno ENOTFOUND
Android connects to mysql database using okhttp
Redis持久化方式RDB和AOF详解

Polynomial Regression (PolynomialFeatures)

DeblurGAN-v2: Deblurring (Orders-of-Magnitude) Faster and Better 图像去模糊
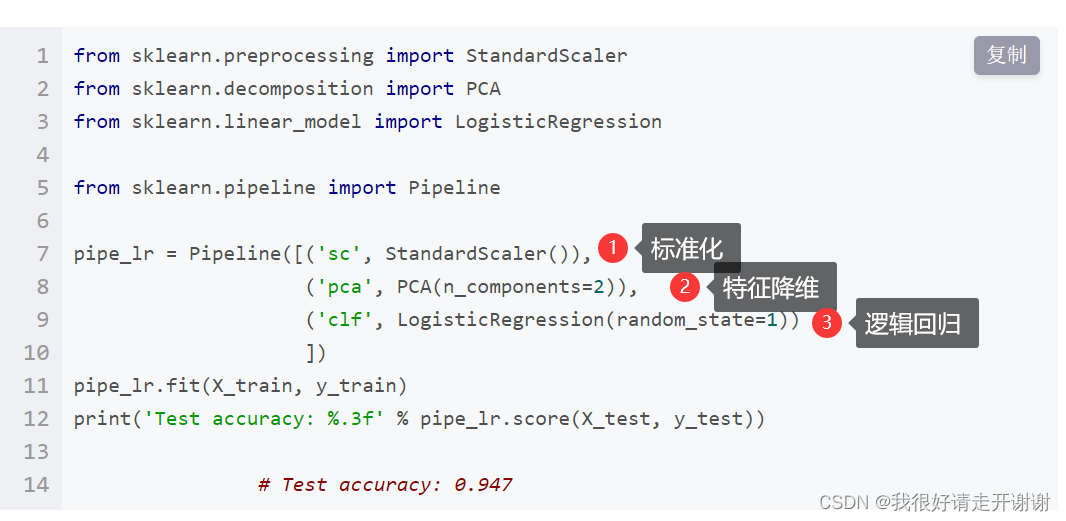
sklearn中的pipeline机制

【CV-Learning】Image Classification

线性回归简介01---API使用案例
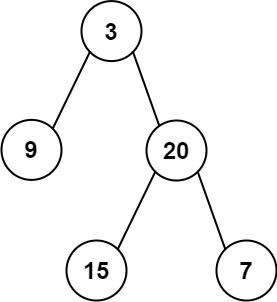
剑指 Offer 2022/7/1
随机推荐
彻底搞懂箱形图分析
【CV-Learning】卷积神经网络
图像resize
Install dlib step pit record, error: WARNING: pip is configured with locations that require TLS/SSL
【深度学习21天学习挑战赛】1、我的手写被模型成功识别——CNN实现mnist手写数字识别模型学习笔记
postgres 递归查询
图像线性融合
Learning curve learning_curve function in sklearn
动手学深度学习__数据操作
SQL练习 2022/7/3
完美解决keyby造成的数据倾斜导致吞吐量降低的问题
Kubernetes基本入门-集群资源(二)
Thoroughly understand box plot analysis
[CV-Learning] Semantic Segmentation
两个APP进行AIDL通信
超详细MySQL总结
(十五)B-Tree树(B-树)与B+树
TensorFlow2 study notes: 7. Optimizer
SQL练习 2022/7/2
with recursive用法
