当前位置:网站首页>How to calculate the distance between two points on the earth (with formula derivation)
How to calculate the distance between two points on the earth (with formula derivation)
2022-08-02 04:02:00 【dumb papa】
前段时间,Read some algorithms for electronic fences,I'm a little confused about one of the codes that calculates the distance between two points on a sphere,Then I found a related algorithm,The relevant calculation formula is recorded in the great circle distance entry of Wikipedia,The general idea is to find the cosine or sine of the central angle corresponding to the arc length between these two points,Then use the inverse trigonometric function to calculate the radians of the central angle,最后求出:弧长=弧度值 × 地球半径.
注:The above picture uses the Baidu map ranging function,Measure the exit of the railway station in Xiangyang City, Hubei Province and the subway in Changchun City, Jilin Province1The distance from Changchun Railway Station North Subway Station where the line passes
一、具体实现
Suppose there are two points on the sphereA(λ1 , φ1)、B(λ2, φ2),λ 和 φ respectively represent their longitudes in the map、纬度,θ 为 AB the corresponding central angle,There are two ways to find the radian corresponding to the arc length of two points on the sphere:
公 式 1 ( 球 面 余 弦 定 理 ) : θ = a c o s ( c o s φ 1 c o s φ 2 c o s ( λ 2 − λ 1 ) + s i n φ 1 s i n φ 2 ) 公式1(Spherical Cosine Theorem):θ = acos(cosφ_1cosφ_2cos(λ_2-λ_1)+sinφ_1sinφ_2) 公式1(球面余弦定理):θ=acos(cosφ1cosφ2cos(λ2−λ1)+sinφ1sinφ2)
公 式 2 ( 半 正 矢 量 公 式 ) : θ = 2 s i n 2 φ 2 − φ 1 2 + c o s φ 1 c o s φ 2 s i n 2 λ 2 − λ 1 2 公式2(Half-positive vector formula):θ = 2\sqrt{sin^2\frac{φ_2-φ_1 }{2}+cosφ_1cosφ_2sin^2\frac{λ_2-λ_1}{2}} 公式2(半正矢量公式):θ=2sin22φ2−φ1+cosφ1cosφ2sin22λ2−λ1
JavaScriptThe calculation of trigonometric functions requires the use of radians,The angle needs to be converted to radians first,具体代码实现如下:
var earchRadius = 6371.009;
function toRadians(degrees) {
return degrees * (Math.PI / 180);
}
// 方法一:Use the spherical cosine law
function getDistance(point1, point2) {
var lat1 = toRadians(point1.lat);
var lat2 = toRadians(point2.lat);
var lngDiffer = toRadians(point1.lng - point2.lng);
var rad = Math.acos(Math.cos(lat1) * Math.cos(lat2) * Math.cos(lngDiffer) + Math.sin(lat1) * Math.sin(lat2));
return rad * earchRadius;
}
// 方法二:Use the half-positive vector formula
function getDistance2(point1, point2) {
var lat1 = toRadians(point1.lat);
var lat2 = toRadians(point2.lat);
var latDiffer = toRadians(point1.lat - point2.lat);
var lngDiffer = toRadians(point1.lng - point2.lng);
var rad = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(latDiffer / 2), 2) + Math.cos(lat1) * Math.cos(lat2) * Math.pow(Math.sin(lngDiffer / 2), 2)));
return rad * earchRadius;
}
注:The average radius of the Earth is approx6,371.009千米,Later in the formula derivation will beR 表示.
下面我们可以验证一下,Let the exit of Xiangyang Railway Station in Xiangyang City, Hubei Province on the map beA点(112.162432,32.064491),A subway in Changchun, Jilin Province1The Changchun Railway Station North Subway Station, which the line passes through, is B点(125.329974,43.919799),The results by the above calculation are as follows:
This matches the distance measured in our opening diagram.
二、公式推导
1、Add auxiliary lines to construct right triangles
从A、BFrom two points, two rays are drawn perpendicular to the equatorial plane,垂足为A1、B1;过 A 向 BB1做垂线,垂足为H.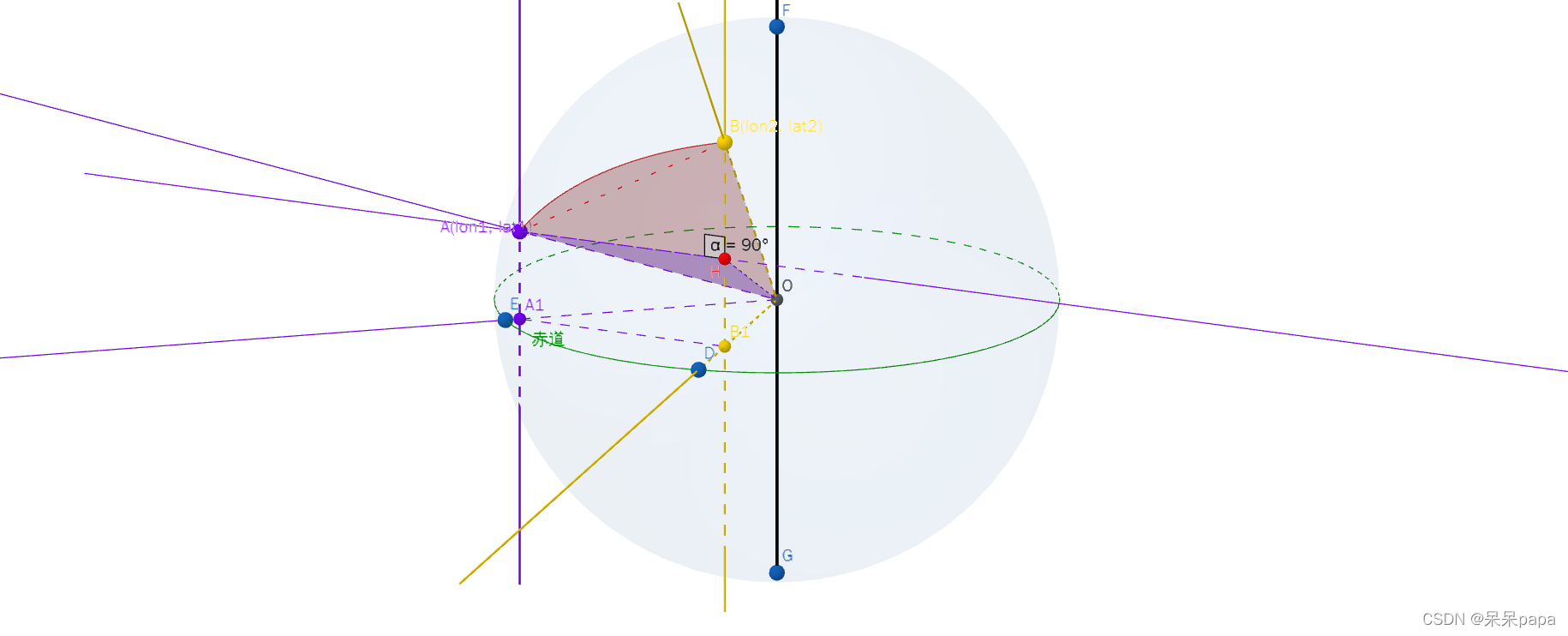
利用△AHBSolve with the cosine law,具体过程如下:
已知∠BOB1为Bpoint latitude value,∠AOA1为Apoint latitude value;∠AOH、∠A1OB1为B点和AThe difference between the longitudes of the points,则有
O B 1 = R × c o s ∠ B O B 1 , O A 1 = R × c o s ∠ A O A 1 OB_1 = R×cos∠BOB_1,OA_1 = R×cos∠AOA_1 OB1=R×cos∠BOB1,OA1=R×cos∠AOA1
B B 1 = R × s i n ∠ B O B 1 , A A 1 = R × s i n ∠ A O A 1 BB_1 = R×sin∠BOB_1,AA_1 = R×sin∠AOA_1 BB1=R×sin∠BOB1,AA1=R×sin∠AOA1
B H = B B 1 − H B 1 = B B 1 − A A 1 BH = BB_1 - HB_1 = BB_1 - AA_1 BH=BB1−HB1=BB1−AA1
B H = R s i n ∠ B O B 1 − R s i n ∠ A O A 1 BH = Rsin∠BOB_1 - Rsin∠AOA_1 BH=Rsin∠BOB1−Rsin∠AOA1
A H 2 = A 1 B 1 2 AH^2 = A_1B_1^2 AH2=A1B12
A H 2 = O B 1 2 + O A 1 2 − 2 O B 1 O A 1 c o s ∠ A 1 O B 1 AH^2 = OB_1^2 + OA_1^2 - 2OB_1OA_1cos∠A_1OB_1 AH2=OB12+OA12−2OB1OA1cos∠A1OB1
A H 2 = R 2 c o s 2 ∠ B O B 1 + R 2 c o s 2 ∠ A O A 1 − 2 R 2 c o s ∠ B O B 1 c o s ∠ A O A 1 c o s λ 2 − λ 1 AH^2 = R^2cos^2∠BOB_1+R^2cos^2∠AOA_1-2R^2cos∠BOB_1cos∠AOA_1cosλ_2-λ_1 AH2=R2cos2∠BOB1+R2cos2∠AOA1−2R2cos∠BOB1cos∠AOA1cosλ2−λ1
A B 2 = A H 2 + B H 2 AB^2 = AH^2 + BH^2 AB2=AH2+BH2
A B 2 = A H 2 + R 2 s i n 2 ∠ B O B 1 + R 2 s i n 2 ∠ A O A 1 − 2 R 2 s i n ∠ B O B 1 s i n ∠ A O A 1 AB^2= AH^2 + R^2sin^2∠BOB_1 + R^2sin^2∠AOA_1 - 2R^2sin∠BOB_1sin∠AOA_1 AB2=AH2+R2sin2∠BOB1+R2sin2∠AOA1−2R2sin∠BOB1sin∠AOA1
A B 2 = 2 R 2 − 2 R 2 ( s i n ∠ B O B 1 s i n ∠ A O A 1 + c o s ∠ B O B 1 c o s ∠ A O A 1 c o s ( λ 2 − λ 1 ) ) AB^2= 2R^2 - 2R^2 (sin∠BOB_1sin∠AOA_1+cos∠BOB_1cos∠AOA_1cos(λ_2-λ_1)) AB2=2R2−2R2(sin∠BOB1sin∠AOA1+cos∠BOB1cos∠AOA1cos(λ2−λ1))
在△AOB中,AB2 = R2 + R2 - 2R2cosθ,故可以计算出 θ 的余弦值:
c o s θ = s i n ∠ B O B 1 s i n ∠ A O A 1 + c o s ∠ B O B 1 c o s ∠ A O A 1 c o s △ λ cosθ = sin∠BOB_1sin∠AOA_1+cos∠BOB_1cos∠AOA_1cos△λ cosθ=sin∠BOB1sin∠AOA1+cos∠BOB1cos∠AOA1cos△λ
即
c o s θ = c o s φ 1 c o s φ 2 c o s ( λ 2 − λ 1 ) + s i n φ 1 s i n φ 2 cosθ = cosφ_1cosφ_2cos(λ_2-λ_1)+sinφ_1sinφ_2 cosθ=cosφ1cosφ2cos(λ2−λ1)+sinφ1sinφ2
This is also the cosine law of spherical triangles.
2、The distance between two points in a 3D coordinate system

Create a coordinate system as shown in the figure,其中ZThe axis coincides with the earth axis,XOYThe plane is the plane where the equator is located,XOZThe plane is the plane of the prime meridian,则可计算:
A 为 ( R c o s φ 1 c o s λ 1 , R c o s φ 1 s i n λ 1 , R s i n φ 1 ) A为(Rcosφ_1cosλ_1,Rcosφ_1sinλ_1,Rsinφ_1) A为(Rcosφ1cosλ1,Rcosφ1sinλ1,Rsinφ1)
B 为 ( R c o s φ 2 c o s λ 2 , R c o s φ 2 s i n λ 2 , R s i n φ 2 ) B为(Rcosφ_2cosλ_2,Rcosφ_2sinλ_2,Rsinφ_2) B为(Rcosφ2cosλ2,Rcosφ2sinλ2,Rsinφ2)
△ X = X B − X A = R c o s φ 2 c o s λ 2 − R c o s φ 1 c o s λ 1 △X = X_B - X_A = Rcosφ_2cosλ_2 - Rcosφ_1cosλ_1 △X=XB−XA=Rcosφ2cosλ2−Rcosφ1cosλ1
△ Y = Y B − Y A = R c o s φ 2 s i n λ 2 − R c o s φ 1 s i n λ 1 △Y = Y_B - Y_A = Rcosφ_2sinλ_2 - Rcosφ_1sinλ_1 △Y=YB−YA=Rcosφ2sinλ2−Rcosφ1sinλ1
△ Z = Z B − Z A = R s i n φ 2 − R s i n φ 1 △Z = Z_B - Z_A = Rsinφ_2 - Rsinφ_1 △Z=ZB−ZA=Rsinφ2−Rsinφ1
∣ A B ∣ = △ Z 2 + △ Y 2 + △ X 2 |AB| = \sqrt{△Z^2+△Y^2+△X^2} ∣AB∣=△Z2+△Y2+△X2
故 c o s θ = ∣ O A ∣ 2 + ∣ O B ∣ 2 − ∣ A B ∣ 2 2 ∣ O A ∣ ∣ O B ∣ cosθ = \frac{|OA|^2 + |OB|^2 - |AB|^2}{2|OA||OB|} cosθ=2∣OA∣∣OB∣∣OA∣2+∣OB∣2−∣AB∣2 ,即 c o s θ = 1 − △ Z 2 + △ Y 2 + △ X 2 2 R 2 cosθ = 1 - \frac{△Z^2+△Y^2+△X^2}{2R^2} cosθ=1−2R2△Z2+△Y2+△X2
化简后的结果为
c o s θ = c o s φ 1 c o s φ 2 c o s ( λ 2 − λ 1 ) + s i n φ 1 s i n φ 2 cosθ = cosφ_1cosφ_2cos(λ_2-λ_1)+sinφ_1sinφ_2 cosθ=cosφ1cosφ2cos(λ2−λ1)+sinφ1sinφ2
注:This method is briefly described in Wikipedia,The final simplification result is also the spherical cosine theorem
3、The haversine formula for a spherical triangle
Just getting started with the semi-positive vector formula,我也是一脸懵.There is no derivation about this formula in a lot of online searches,Until I saw an article on Douban半正矢公式,The semi-positive vector formula is deduced in the article using geometrical methods,Then someone in the comment area pointed out that the haversine function can be substituted into the spherical cosine theorem,我这才恍然大悟.In fact, this formula is not difficult,Still using the half-width formula at all.
Here we need to use the sine vector that is basically not used in trigonometric functions、Haversine function:
v e r s i n θ = 2 s i n 2 ( θ 2 ) = 1 − c o s θ ( 正 矢 ) versinθ = 2sin^2(\frac{θ}{2}) = 1 - cosθ (正矢) versinθ=2sin2(2θ)=1−cosθ(正矢)
h a v e r s i n θ = v e r s i n θ 2 = 1 − c o s θ 2 ( 半 正 矢 ) haversinθ = \frac{versinθ}{2} = \frac{1-cosθ}{2} (半正矢) haversinθ=2versinθ=21−cosθ(半正矢)
From this, the equation can be obtained: s i n 2 ( θ 2 ) = 1 − c o s θ 2 sin^2(\frac{θ}{2}) = \frac{1-cosθ}{2} sin2(2θ)=21−cosθ
然后,Calculated using the previous two methods cosθ Substitute the value into the equation:
s i n 2 ( θ 2 ) = 1 − 1 + △ Z 2 + △ Y 2 + △ X 2 2 R 2 2 sin^2(\frac{θ}{2}) = \frac{1-1+\frac{△Z^2+△Y^2+△X^2}{2R^2}}{2} sin2(2θ)=21−1+2R2△Z2+△Y2+△X2
由于 R2 Can be removed after expansion,The following calculations are not written R2 了.
s i n 2 ( θ 2 ) = △ Z 2 + △ Y 2 + △ X 2 4 sin^2(\frac{θ}{2}) = \frac{△Z^2+△Y^2+△X^2}{4} sin2(2θ)=4△Z2+△Y2+△X2
s i n 2 ( θ 2 ) = 2 − 2 s i n φ 1 s i n φ 2 − 2 c o s φ 1 c o s φ 2 c o s ( λ 2 − λ 1 ) 4 ( 公 式 1 ) sin^2(\frac{θ}{2}) = \frac{2-2sinφ_1sinφ_2-2cosφ_1cosφ_2cos(λ_2-λ_1) }{4} (公式1) sin2(2θ)=42−2sinφ1sinφ2−2cosφ1cosφ2cos(λ2−λ1)(公式1)
Here we use the product and difference formula in trigonometric functions:
s i n φ 1 s i n φ 2 = c o s ( φ 2 − φ 1 ) − c o s ( φ 2 + φ 1 ) 2 sinφ_1sinφ_2 = \frac{cos(φ_2-φ_1)-cos(φ_2+φ_1)}{2} sinφ1sinφ2=2cos(φ2−φ1)−cos(φ2+φ1)
Continue to expand using the square and formula c o s ( φ 2 + φ 1 ) cos(φ_2+φ_1) cos(φ2+φ1) 得:
s i n φ 1 s i n φ 2 = c o s ( φ 2 − φ 1 ) + s i n φ 2 s i n φ 1 − c o s φ 2 c o s φ 1 ) 2 sinφ_1sinφ_2 = \frac{cos(φ_2-φ_1)+sinφ_2sinφ_1-cosφ_2cosφ_1)}{2} sinφ1sinφ2=2cos(φ2−φ1)+sinφ2sinφ1−cosφ2cosφ1)
代入公式1中,可得:
s i n 2 ( θ 2 ) = 2 − c o s ( φ 2 − φ 1 ) + c o s φ 1 c o s φ 2 − s i n φ 1 s i n φ 2 − 2 c o s φ 1 c o s φ 2 c o s ( λ 2 − λ 1 ) 4 sin^2(\frac{θ}{2}) = \frac{2-cos(φ_2-φ_1)+cosφ_1cosφ_2-sinφ_1sinφ_2-2cosφ_1cosφ_2cos(λ_2-λ_1) }{4} sin2(2θ)=42−cos(φ2−φ1)+cosφ1cosφ2−sinφ1sinφ2−2cosφ1cosφ2cos(λ2−λ1)
s i n 2 ( θ 2 ) = 2 − c o s ( φ 2 − φ 1 ) − c o s φ 1 c o s φ 2 − s i n φ 1 s i n φ 2 + 2 c o s φ 1 c o s φ 2 [ 1 − c o s ( λ 2 − λ 1 ) ] 4 sin^2(\frac{θ}{2}) = \frac{2-cos(φ_2-φ_1)-cosφ_1cosφ_2-sinφ_1sinφ_2+2cosφ_1cosφ_2[1-cos(λ_2-λ_1)] }{4} sin2(2θ)=42−cos(φ2−φ1)−cosφ1cosφ2−sinφ1sinφ2+2cosφ1cosφ2[1−cos(λ2−λ1)]
s i n 2 ( θ 2 ) = 2 − c o s ( φ 2 − φ 1 ) − ( c o s φ 1 c o s φ 2 + s i n φ 1 s i n φ 2 ) + 2 c o s φ 1 c o s φ 2 [ 1 − c o s ( λ 2 − λ 1 ) ] 4 sin^2(\frac{θ}{2}) = \frac{2-cos(φ_2-φ_1)-(cosφ_1cosφ_2+sinφ_1sinφ_2)+2cosφ_1cosφ_2[1-cos(λ_2-λ_1)] }{4} sin2(2θ)=42−cos(φ2−φ1)−(cosφ1cosφ2+sinφ1sinφ2)+2cosφ1cosφ2[1−cos(λ2−λ1)]
s i n 2 ( θ 2 ) = 2 − 2 c o s ( φ 2 − φ 1 ) + 2 c o s φ 1 c o s φ 2 [ 1 − c o s ( λ 2 − λ 1 ) ] 4 sin^2(\frac{θ}{2}) = \frac{2-2cos(φ_2-φ_1)+2cosφ_1cosφ_2[1-cos(λ_2-λ_1)] }{4} sin2(2θ)=42−2cos(φ2−φ1)+2cosφ1cosφ2[1−cos(λ2−λ1)]
s i n 2 ( θ 2 ) = 1 − c o s ( φ 1 − φ 2 ) 2 + c o s φ 1 c o s φ 2 1 − c o s ( λ 2 − λ 1 ) 2 sin^2(\frac{θ}{2}) = \frac{1-cos(φ_1-φ_2) }{2}+cosφ_1cosφ_2\frac{1-cos(λ_2-λ_1)}{2} sin2(2θ)=21−cos(φ1−φ2)+cosφ1cosφ221−cos(λ2−λ1)
Finally, use the half-width formula:
s i n 2 ( θ 2 ) = s i n 2 φ 2 − φ 1 2 + c o s φ 1 c o s φ 2 s i n 2 λ 2 − λ 1 2 sin^2(\frac{θ}{2}) = sin^2\frac{φ_2-φ_1 }{2}+cosφ_1cosφ_2sin^2\frac{λ_2-λ_1}{2} sin2(2θ)=sin22φ2−φ1+cosφ1cosφ2sin22λ2−λ1
三、总结一下
总的来说,Calculating the distance between two points on the sphere is probably the two formulas above:Spherical cosine law and half-positive vector formula(That is the half angle solution).Using the certificate vector formula can reduce the error of spherical cosine theorem calculation,That is, in order to eliminate the error of the mathematical function when calculating the cosine.The included angle corresponding to the arc length is 0时,The value in radians is1,The result obtained by the arc cosine function is not0,but a close one0的浮点数.
边栏推荐
- PHP8.2将会有哪些新东西?
- Kali环境下Frida编写脚本智能提示
- Stable and easy-to-use short connection generation platform, supporting API batch generation
- vim edit mode
- (4) 函数、Bug、类与对象、封装、继承、多态、拷贝
- CSRF(跨站请求伪造)
- kali安装IDEA
- 2.PHP变量、输出、EOF、条件语句
- ES6 array extension methods map, filter, reduce, fill and array traversal for…in for…of arr.forEach
- 战场:3(双子叶植物)vulnhub走读
猜你喜欢

(1) print()函数、转义字符、二进制与字符编码 、变量、数据类型、input()函数、运算符
(1)Thinkphp6入门、安装视图、模板渲染、变量赋值

Alfa: 1 vulnhub walkthrough
IP门禁:手把手教你用PHP实现一个IP防火墙

hackmyvm: may walkthrough

(3) string

13. JS output content and syntax
VIKINGS: 1 vulnhub walkthrough
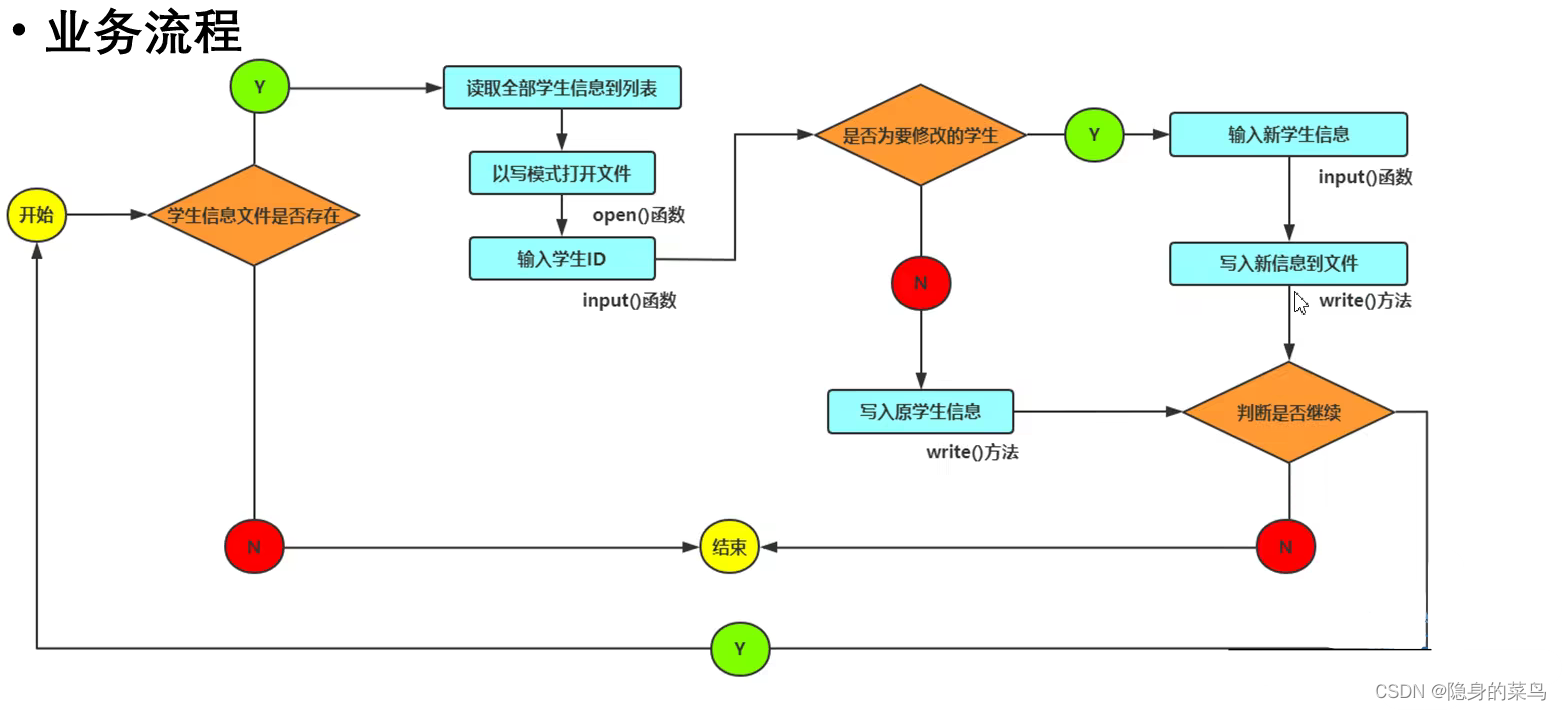
(6) 学生信息管理系统设计
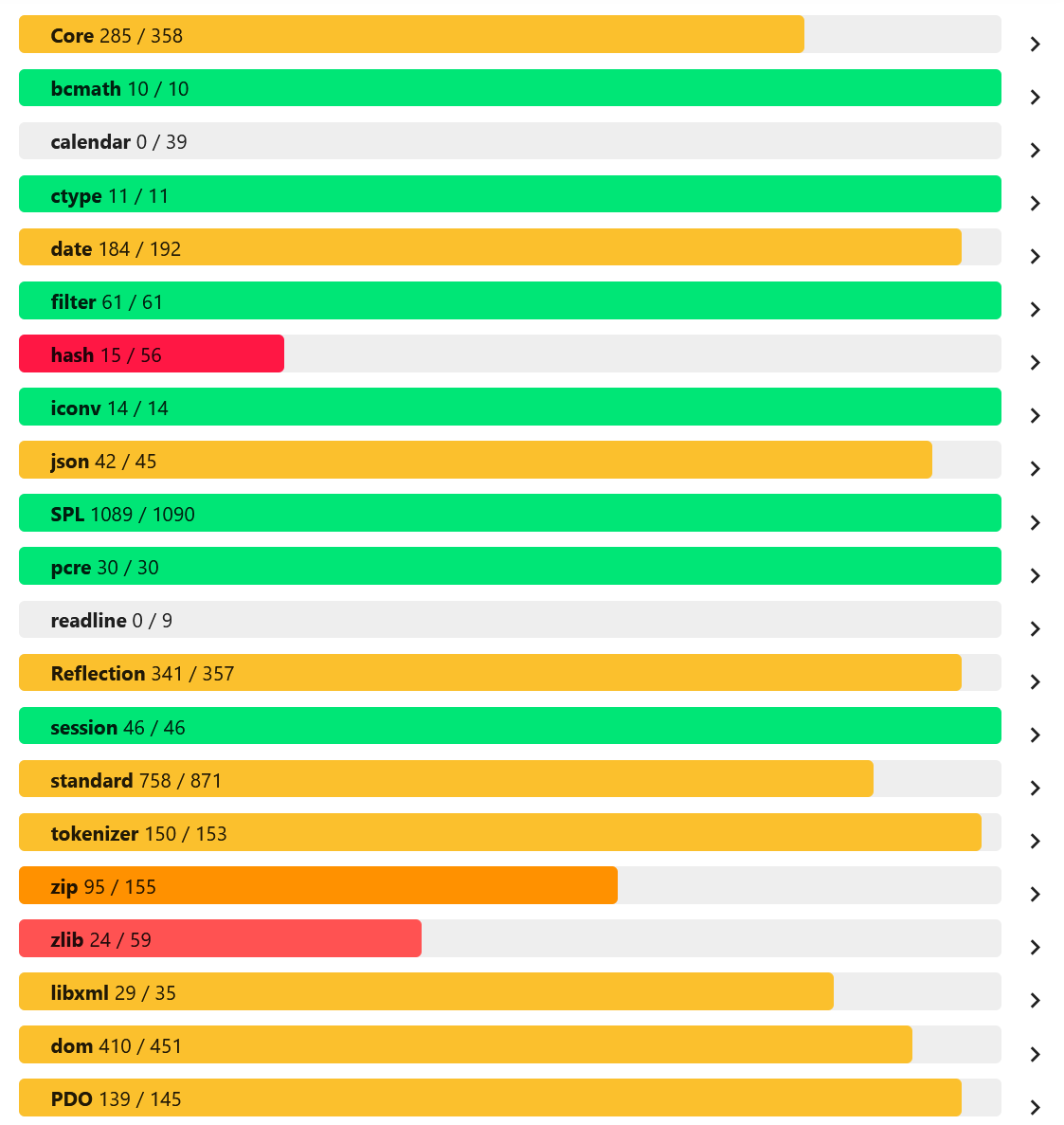
Several interesting ways to open PHP: from basic to perverted
随机推荐
hackmyvm: juggling walkthrough
1.初识PHP
4.表单与输入
[mikehaertl/php-shellcommand] A library for invoking external command operations
CSRF(跨站请求伪造)
2. PHP variables, output, EOF, conditional statements
[sebastian/diff]一个比较两段文本的历史变化扩展库
After the mailbox of the Pagoda Post Office is successfully set up, it can be sent but not received.
(1) the print () function, escape character, binary and character encoding, variables, data type, the input () function, operator
17.JS条件语句和循环,以及数据类型转换
[league/flysystem]一个优雅且支持度非常高的文件操作接口
13. JS output content and syntax
Basic use of v-on, parameter passing, modifiers
hackmyvm-hopper预排
(7) superficial "crawlers" process (concept + practice)
PHP基金会三月新闻公告发布
[sebastian/diff] A historical change extension library for comparing two texts
文件包含漏洞
(2) Thinkphp6 template engine ** tag
一个网络安全小白鼠的学习之路—nmap高级用法之脚本使用