当前位置:网站首页>D39_Eulerian Angles and Quaternions
D39_Eulerian Angles and Quaternions
2022-08-05 06:32:00 【Not so simple GG】
Table of Contents
5. Cross product of quaternions
1. Euler Angles
Consists of three angles (x, y, z), which are used to describe the rotation of an object in a specific coordinate system
The rotation adjusted by the Inspector panel is the Euler angle transform.eulerAngles
Eulerian angles are intuitive and easy to understand, but one disadvantage is the universal lock (please encyclopedia)
Unity uses y→x→z
2. Quaternion
Quaternion
A quaternion consists of a scalar and a 3D element [w,(x,y,z)]
Meaning: Represents a rotation in 3D space
Given the rotation, assuming that the rotation is about the N axis, the rotation is θ degrees, and the N axis is (x, y, z), then it constitutes a quaternion
Q=[cos(θ/2),sin(θ/2)*x,sin(θ/2)*y,sin(θ/2)*z]
Constructing a quaternion from axis-angle pairs Quaternion.AngleAxis
Euler angle conversion to quaternion Quaternion.Euler
Quaternion to Euler Angles .eulerAngles
3. Negative Quaternion
q[w,(x,y,z)] -q[-w,(-x,-y,-z)]
Geometric meaning: q and -q represent the same amount of rotation
4.Unit Quaternion
q[1,0,0,0] -q[-1,0,0,0]
Quaternion.identity
Geometric meaning: represents a quaternion without a rotation angle
5. QuaternionThe cross product of
The result obtained by multiplying a quaternion by a quaternion is still a quaternion
Geometric meaning: The new quaternion obtained by the cross product of two quaternions is the superposition of the two quaternion rotations
transform.rotation*=Quaternion.AngleAxis();
The cross product of a quaternion and a vector can get a new vector that rotates according to the rotation direction of the quaternion
Note: Only the quaternion * vector operator is overloaded in the quaternion, and there is no overloaded vector * quaternion operator, so only
Vector3 dir=Quaternion.AngleAxis()*Vector3.forward;
Quaternion.LookRotation(); Passing a vector as a parameter can get the angle required to turn the positive direction of the object to the vector
6. Quaterniondifference
Quaternion.Slerp(a,b,t);
边栏推荐
- DevOps process demo (practical record)
- 初识网页与浏览器
- VRRP overview and experiment
- spark source code - task submission process - 3-ApplicationMaster
- js dynamically get screen width and height
- VRRP概述及实验
- 网络排错基础-学习笔记
- Programmers should understand I/O this way
- VLAN is introduced with the experiment
- product learning materials
猜你喜欢
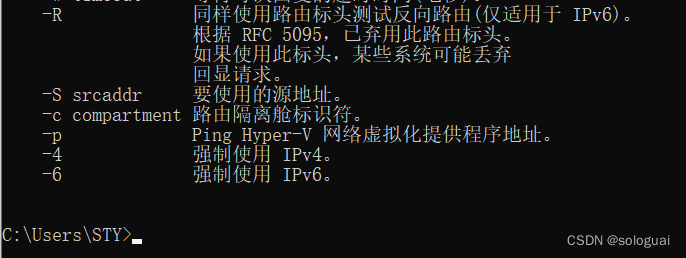
网络层协议介绍
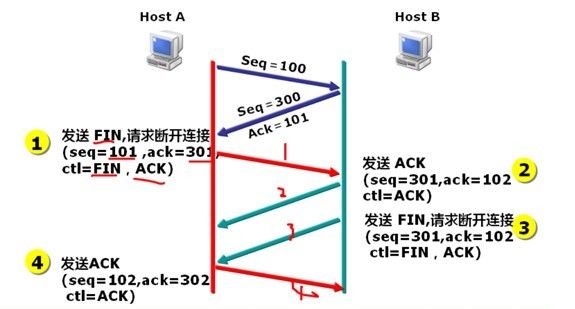
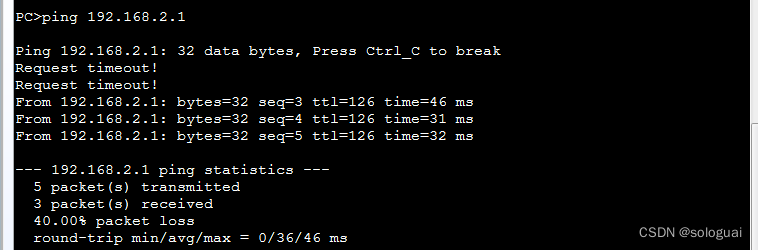
网络不通?服务丢包?看这篇就够了

系统基础-学习笔记(一些命令记录)
VRRP概述及实验
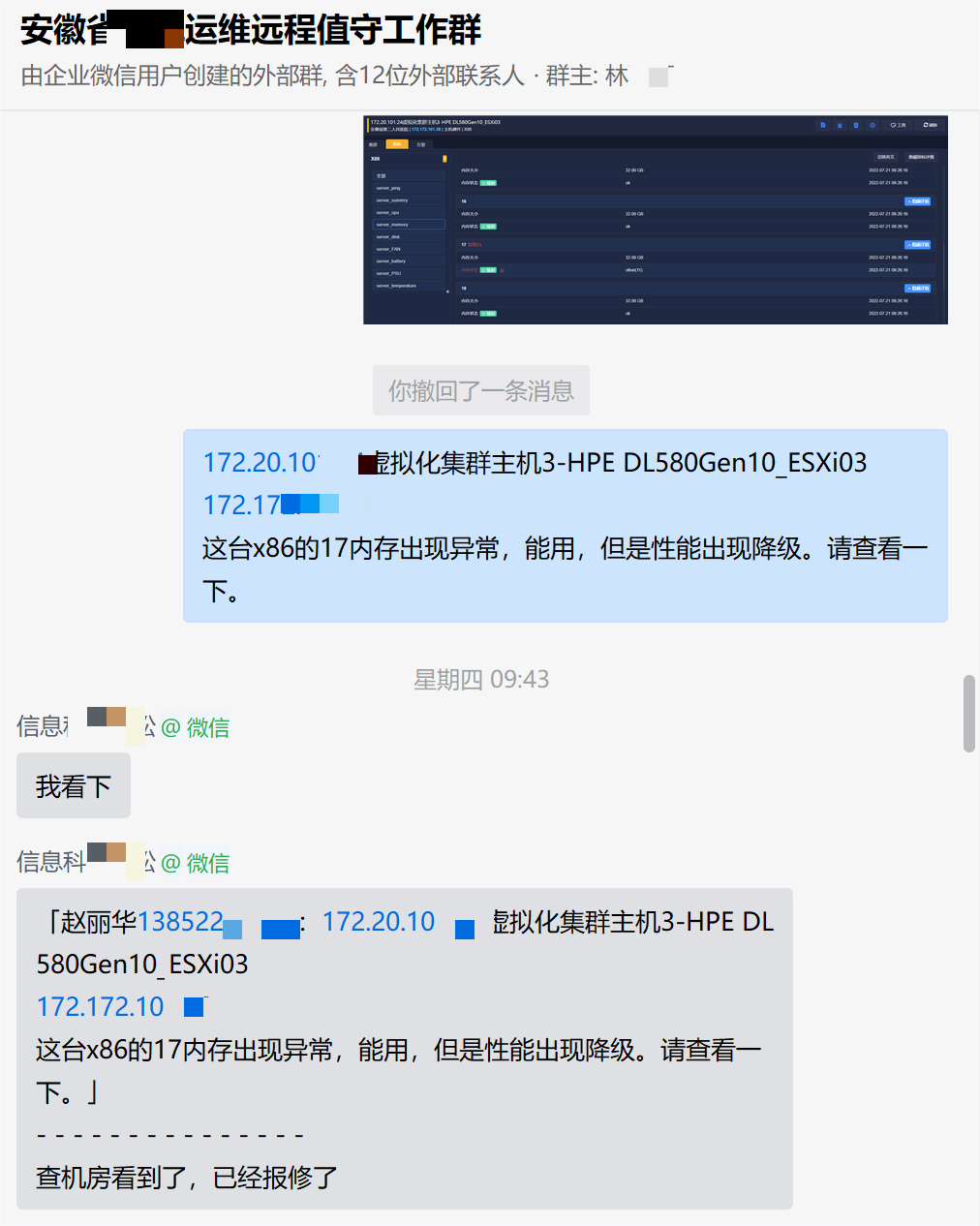
By solving these three problems, the operation and maintenance efficiency will exceed 90% of the hospital
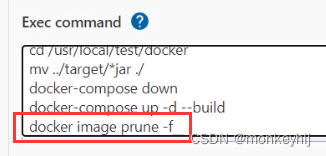
DevOps process demo (practical record)

实力卷王LinkSLA,实现运维工程师快乐摸鱼

What are some things that you only know when you do operation and maintenance?
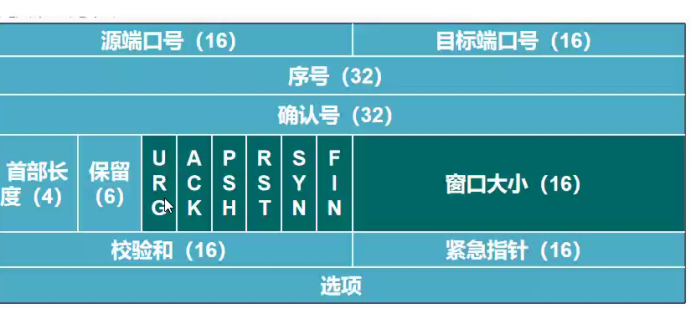
传输层协议
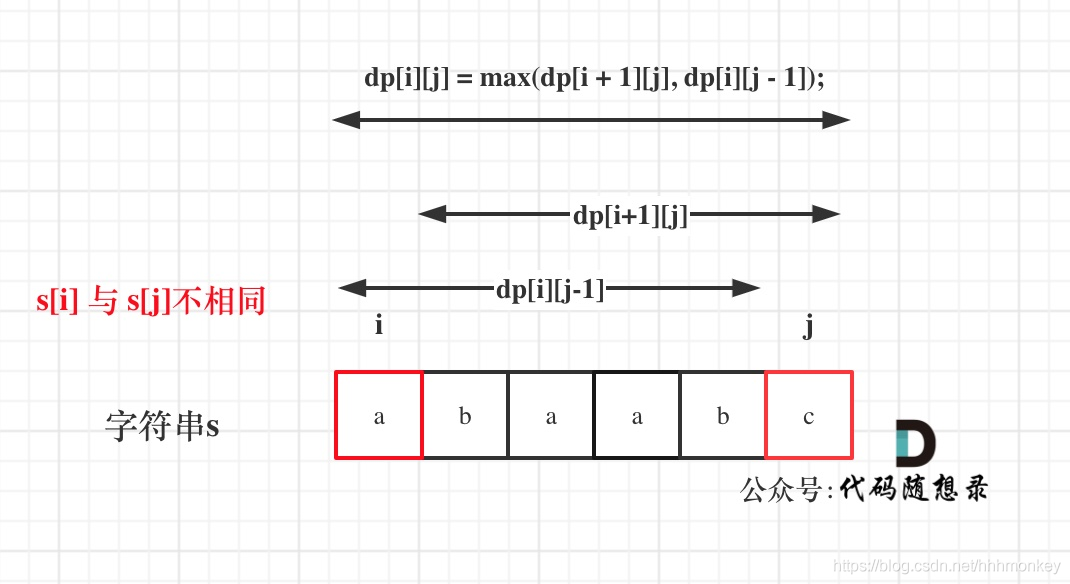
LeetCode练习及自己理解记录(1)
随机推荐
ROS2下使用ROS1 bag的方法
What?CDN cache acceleration only works for accelerating static content?
LinkSLA坚持用户第一,打造可持续的运维服务方案
The Servlet to jump to the JSP page, forwarding and redirection
I/O performance and reliability
The size of the screen adaptation
大小屏适配
网络不通?服务丢包?看这篇就够了
static routing
link 和@improt的区别
智能运维会取代人工运维吗?
原生JS带你了解数组方法实现及使用
What should I do if the SSL certificate prompts that it is expired or invalid?
el-autocomplete use
Proprietary host CDH
Seven Ways to Center a Box Horizontally and Vertically
What are some things that you only know when you do operation and maintenance?
Spark source code-task submission process-6.2-sparkContext initialization-TaskScheduler task scheduler
DevOps-了解学习
[问题已处理]-jenkins流水线checkout超时