当前位置:网站首页>The 19th Zhejiang Provincial College Programming Contest VP record + supplementary questions
The 19th Zhejiang Provincial College Programming Contest VP record + supplementary questions
2022-07-07 23:21:00 【HeartFireY】
| A | B | C | D | E | F | G | H | I | J | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AC | AC | AC | – | – | WA/ Supplementary questions | AC | – | AC | AC/ await a vacancy or job opening | – | AC | AC |
A.JB Loves Math
Topic analysis
Now there are two numbers a a a and b b b, It's up to you to choose an odd number x x x And even numbers y y y, You can give it every time a a a Add x x x Or minus y y y, Ask the minimum number of operations will a a a Turn into b b b.
Just discuss the difference by classification .
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
inline void solve(){
int a, b; cin >> a >> b;
int det = abs(a - b);
if(a == b) cout << 0 << endl;
else if(a > b && (det & 1 == 0) || a < b && det & 1) cout << 1 << endl;
else if(a < b && (det / 2) & 1 || a > b) cout << 2 << endl;
else cout << 3 << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
int t = 0; cin >> t;
while(t--) solve();
return 0;
}
B.JB Loves Comma
Topic analysis
find cjb Then add a comma , Examples 2 Praise
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
inline void solve(){
string str; cin >> str;
for(int i = 0; i < str.size(); i++){
if(i >= 2 && str[i] == 'b' && str[i - 1] == 'j' && str[i - 2] == 'c') cout << str[i] << ',';
else cout << str[i];
}
}
signed main(){
solve();
return 0;
}
C.JB Wants to Earn Big Money
Topic analysis
Directly according to the meaning of the simulation , Just count two kinds of quantity .
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
inline void solve(){
int n, m, X; cin >> n >> m >> X;
int ans = 0;
for(int i = 1; i <= n; i++){
int s; cin >> s;
if(s >= X) ans++;
}
for(int i = 1; i <= m; i++){
int s; cin >> s;
if(s <= X) ans++;
}
cout << ans << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
F.Easy Fix
Topic analysis
The chairman tree is hanging , It didn't come out during the game , I'm a vegetable dog
Given the permutation p 1 , p 2 , p 3 , … , p n p_1, p_2, p_3,\dots, p_n p1,p2,p3,…,pn, Definition A i A_i Ai It means that p i p_i pi Left side parallel p i p_i pi The number of small numbers , B i B_i Bi It means that p i p_i pi The right side is not bigger than p i p_i pi The number of small numbers , C i = min ( A i , B i ) C_i = \min(A_i, B_i) Ci=min(Ai,Bi). Now, given multiple operations ( l , r ) (l, r) (l,r), Ask for each operation , In exchange for ( p i , p j ) (p_i, p_j) (pi,pj) After ∑ C i \sum C_i ∑Ci.
First consider how to deal with the initial C i C_i Ci value , The following properties were observed :
- about A i A_i Ai The solution process of value is similar to the idea of finding reverse order pairs , You can maintain the tree array directly , O ( n log n ) O(n\log n) O(nlogn) Get all A i A_i Ai
- Because it's permutation , B i = p i − 1 − A i B_i = p_i - 1 - A_i Bi=pi−1−Ai Sure O ( 1 ) O(1) O(1) Get
- that C i = min ( A i , B i ) C_i = \min(A_i, B_i) Ci=min(Ai,Bi) It's also O ( 1 ) O(1) O(1) Got
Because each inquiry is independent , Then consider exchanging ( p l , p r ) (p_l, p_r) (pl,pr) Operation of C i C_i Ci Influence :
about [ 1 , l ) , ( r , n ] [1, l), (r , n] [1,l),(r,n] Number of ranges , C i C_i Ci Value must not affect . Because the switching operation is carried out on one side
about p l p_l pl, Exchange to r r r After the position , A l → A l + District between [ l , r ] Small On p l Of Count word individual Count A_l \rightarrow A_l + Section [l,r] Less than p_l The number of the number of Al→Al+ District between [l,r] Small On pl Of Count word individual Count , B l ’ B_l’ Bl’ You can still ask directly
about p r p_r pr, Exchange to l l l After the position , A r → A r − District between [ l , r ] Small On p r Of Count word individual Count A_r \rightarrow A_r - Section [l ,r] Less than p_r The number of the number of Ar→Ar− District between [l,r] Small On pr Of Count word individual Count , B r ’ B_r’ Br’ You can still ask directly
If we ask online ( Chairman tree maintenance ), So for p l , p r p_l,p_r pl,pr, In fact, it can be directly two O ( l o g n ) O(logn) O(logn) Ask again .
So the point is for [ l + 1 , r − 1 ] [l + 1, r - 1] [l+1,r−1] The number in the interval C i C_i Ci Value change , How to maintain ?
about p l ≤ p i ≤ p r p_l \leq p_i \leq p_r pl≤pi≤pr, If A i ≤ B i A_i \leq B_i Ai≤Bi, After exchange A i − 1 , B i + 1 A_i - 1, B_i + 1 Ai−1,Bi+1, thus C i − 1 C_i - 1 Ci−1
about p l ≥ p i ≥ p r p_l \geq p_i \geq p_r pl≥pi≥pr, If A i ≥ B i A_i \geq B_i Ai≥Bi, After exchange A i + 1 , B i − 1 A_i + 1, B_i - 1 Ai+1,Bi−1, thus C i − 1 C_i -1 Ci−1
about p l ≤ p i ≤ p r p_l \leq p_i \leq p_r pl≤pi≤pr, If A i − 1 ≥ B i + 1 , A i ≥ B i A_i - 1 \geq B_i + 1, A_i \geq B_i Ai−1≥Bi+1,Ai≥Bi, After exchange C i + 1 C_i + 1 Ci+1
about p l ≥ p i ≥ p r p_l \geq p_i \geq p_r pl≥pi≥pr, If A i − 1 ≤ B i + 1 , A i ≤ B i A_i - 1 \leq B_i + 1, A_i \leq B_i Ai−1≤Bi+1,Ai≤Bi, After exchange C i + 1 C_i + 1 Ci+1
So for the above four cases , We can use four chairman trees for maintenance . meanwhile , about p l , p r p_l, p_r pl,pr The contribution calculation of also needs to support the interval < K <K <K Number of numbers query , Therefore, a total of five chairman trees are required for maintenance , Complexity O ( m × 4 log n ) O(m \times 4 \log n) O(m×4logn).
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
const int N = 1e5 + 10;
int p[N], a[N], b[N], c[N], d[N];
using bset5 = std::bitset<5>;
namespace Fenwick{
int tree[N], len;
#define lowbit(x) ((x) & (-x))
inline void init(int ln){
len = ln; }
inline void update(int i, int x){
for(int pos = i; pos <= len; pos += lowbit(pos)) tree[pos] += x; }
inline int getsum(int i, int ans = 0){
for(int pos = i; pos; pos -= lowbit(pos)) ans += tree[pos]; return ans; }
}
namespace PresidentTree{
int root[N], sum[N << 5][5], lc[N << 5], rc[N << 5], cnt;
#define ls l, mid
#define rs mid + 1, r
void update(int &rt, int pre, int l, int r, int x, bset5 inc){
rt = ++cnt, lc[rt] = lc[pre], rc[rt] = rc[pre];
for(int i = 0; i <= 5; i++) sum[rt][i] = sum[pre][i] + (inc[i] ? 1 : 0);
if(l == r) return;
int mid = l + r >> 1;
if(x <= mid) update(lc[rt], lc[rt], l, mid, x, inc);
else update(rc[rt], rc[rt], mid + 1, r, x, inc);
}
int query(int st, int ed, int l, int r, int L, int R, int id){
if(l == L && r == R) return sum[ed][id] - sum[st][id];
int mid = l + r >> 1;
if(mid >= R) return query(lc[st], lc[ed], l, mid, L, R, id);
else if(mid >= L) return query(lc[st], lc[ed], l, mid, L, mid, id) + query(rc[st], rc[ed], mid + 1, r, mid + 1, R, id);
else return query(rc[st], rc[ed], mid + 1, r, L, R, id);
}
}
#define Pdt PresidentTree
inline void solve(){
int n = 0; std::cin >> n;
Fenwick::init(n);
for(int i = 1; i <= n; i++) std::cin >> p[i];
for(int i = 1; i <= n; i++){
a[i] = Fenwick::getsum(p[i]);
b[i]= p[i] - 1 - a[i];
Fenwick::update(p[i], 1);
c[i] = std::min(a[i], b[i]);
d[i] = d[i - 1] + c[i];
}
for(int i = 1; i <= n; i++){
bset5 flag; flag.reset();
if(a[i] <= b[i]) flag[1] = true;
if(a[i] >= b[i]) flag[3] = true;
if(a[i] - 1 >= b[i] + 1 && a[i] >= b[i]) flag[2] = true;
if(a[i] + 1 <= b[i] - 1 && a[i] <= b[i]) flag[4] = true;
flag[0] = true;
Pdt::update(Pdt::root[i], Pdt::root[i - 1], 1, n + 1, p[i], flag);
}
int m = 0; std::cin >> m;
while(m--){
int l, r; std::cin >> l >> r;
if(l == r){
std::cout << d[n] << endl; continue; }
else if(l > r) std::swap(l, r);
int ans = d[n] - c[l] - c[r];
if(p[l] < p[r]){
ans -= Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[l], p[r], 1)
- Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[l], p[r], 2);
} else {
ans -= Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[r], p[l], 3)
- Pdt::query(Pdt::root[l], Pdt::root[r - 1], 1, n + 1, p[r], p[l], 4);
}
int nowa = Pdt::query(Pdt::root[0], Pdt::root[l - 1], 1, n + 1, 1, p[r], 0),
nowb = p[r] - 1 - nowa;
ans += std::min(nowa, nowb);
nowa = Pdt::query(Pdt::root[r], Pdt::root[n], 1, n + 1, 1, p[l], 0),
nowb = p[l] - 1 - nowa;
ans += std::min(nowa, nowb);
std::cout << ans << endl;
}
}
signed main(){
std::ios_base::sync_with_stdio(false), std::cin.tie(0);
solve();
return 0;
}
G.Easy Glide
Topic analysis
Given the starting point and ending point on the two-dimensional plane , as well as n n n A ski spot , Start from the starting point with v 1 v_1 v1 Speed walking , arrive n n n One of the ski spots can be followed by v 2 v_2 v2 walk 3 s 3s 3s, Then back to v 1 v_1 v1. It is required to find the shortest time from the beginning to the end .
The starting point is set to 0 0 0 spot , The end point is set to n + 1 n + 1 n+1 spot , The starting point is full of edges towards other points , Then all points build edges towards the end , then n n n Points build up sides with each other , Edge weights are all time . then d i j s k t r a dijsktra dijsktra seek 0 0 0 To n + 1 n + 1 n+1 The shortest path is enough .
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e3 + 10;
struct node{
int x, y;
}p[N], st, ed;
struct edge{
int v;
double dis;
};
vector<edge> g[N];
int vis[10005];
inline double getdis(node x, node y){
double ans = sqrt((x.x - y.x) * (x.x - y.x) + (x.y - y.y) * (x.y - y.y));
return ans;
}
struct nd{
int v;
double dis;
const bool operator< (const nd &x) const {
return dis > x.dis; }
};
double dis[1100];
int n = 0;
double dijkstra(){
priority_queue<nd> pq;
pq.emplace(nd{
0, 0});
while(pq.size()){
auto [u,ww] = pq.top(); pq.pop();
if(vis[u]) continue;
vis[u] = 1, dis[u] = ww;
for(auto [v,w] : g[u]){
if(vis[v]) continue;
pq.emplace(nd{
v, ww + w});
}
}
return dis[n + 1];
}
inline void solve(){
cin >> n;
for(int i = 1; i <= n; i++){
int x, y; cin >> p[i].x >> p[i].y;
}
cin >> st.x >> st.y >> ed.x >> ed.y;
double v1, v2; cin >> v1 >> v2;
for(int i = 1; i <= n; i++){
g[0].emplace_back(edge{
i, getdis(st, p[i]) / v1});
}
g[0].emplace_back(edge{
n + 1, getdis(st, ed) / v1});
for(int i = 1; i <= n; i++){
double diss = getdis(p[i], ed), time = 0;
if(diss / v2 > 3.0) time += 3.0, diss -= v2 * 3, time += diss / v1;
else time = diss / v2;
//cout << i << "->" << "ed" << time << endl;
g[i].emplace_back(edge{
n + 1, time});
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
double diss = getdis(p[i], p[j]), time = 0;
if(diss / v2 > 3.0) time += 3.0, diss -= v2 * 3, time += diss / v1;
else time = diss / v2;
g[i].emplace_back(edge{
j, time});
}
}
cout << dijkstra() << endl;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
cout<<fixed<<setprecision(12);
solve();
return 0;
}
I.Barbecue
Topic analysis
Given string , You can choose from both ends each time 1 Delete characters , If it becomes a palindrome string after the operation, enter .
obviously , You need to first judge whether it is a palindrome string at the beginning , Here you can directly hash .
Next , If it's not palindrome at first , We will find the nature :
- If one end of the current string is deleted 1 1 1 Characters will become palindromes , Then be sure to choose the deletion at the other end . Then the answer is related to length parity
- If both ends are deleted, it will change palindromes , Then the present is bound to fail
- But it can be found that deleting both ends will change palindromes , The string length must be even , At this time, the law of parity is satisfied .
Code
#include <bits/stdc++.h>
#define int long long
#define unt unsigned long long
#define endl '\n'
using namespace std;
const unt N = 1e6 + 10, base = 233233, MOD = 1e9 + 7;
unt hashp[N], hash_s1[N], hash_s2[N];
inline void init(){
hashp[0] = 1;
for(int i = 1; i <= N - 5; i++){
hashp[i] = hashp[i - 1] * base;
}
}
inline int check(int l, int r){
unt hash_val1 = hash_s1[r] - hash_s1[l - 1] * hashp[r - l + 1];
unt hash_val2 = hash_s2[l] - hash_s2[r + 1] * hashp[r - l + 1];
return hash_val1 == hash_val2;
}
inline void solve(){
int n, q; cin >> n >> q;
string s; cin >> s; s = '@' + s;
for(int i = 1; i <= n; i++) hash_s1[i] = hash_s1[i - 1] * base + s[i];
for(int i = n; i >= 1; i--) hash_s2[i] = hash_s2[i + 1] * base + s[i];
while(q--){
int l, r; cin >> l >> r;
if(l == r || check(l, r)) cout << "Budada\n";
else if((r - l + 1) & 1) cout << "Putata\n";
else cout << "Budada\n";
}
}
signed main(){
init();
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
J.Frog
Computational geometry , It was written by his teammates , await a vacancy or job opening . Put a code :
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define ull unsigned long long
using namespace std;
const ull base = 13331;
const int N = 6;
const double pi=acos(-1);
int n,q,x,y;
inline void init(){
}
bool fk1(){
for(int i=(x+1)%360,cnt=1,j=(x+359)%360;cnt<=90;cnt++,i=(i+1)%360,j=(j+359)%360){
if(i==y||j==y)return true;
}
return false;
}
int getrotate(){
for(int i=(x+1)%360,cnt=1,j=(x+359)%360;cnt<=360;cnt++,i=(i+1)%360,j=(j+359)%360){
if(j==y)return -cnt;
if(i==y)return cnt;
//cout<<i<<" "<<j<<endl;
}
return 0;
}
bool ck(double x,double y){
return x*x+y*y>=1;
}
pair<double,double> nmb(double sx,double sy,double tx,double ty){
double midx=(sx+tx)/2,midy=(sy+ty)/2;
double d1=sqrt((midx-sx)*(midx-sx)+(midy-sy)*(midy-sy)),d2=sqrt(1-d1*d1);
double dx=sx-midx,dy=sy-midy,ansx=dy*d2/d1,ansy=dx*d2/d1;
//cout<<"???"<<midx<<" "<<midy<<" "<<ansx<<" "<<ansy<<endl;
if(ck(ansx+midx,ansy-midy)){
return {ansx+midx,midy-ansy};
}
else{
return {midx-ansx,midy+ansy};
}
}
inline void solve(){
cin>>x>>y;
double stx=cos(pi*x/180),sty=sin(pi*x/180),edx=cos(pi*y/180),edy=sin(pi*y/180);
if(x==y){
cout<<"0\n"<<stx<<" "<<sty<<endl;
return;
}
int d=getrotate();
if(abs(d)<=90){
cout<<"2\n";
cout<<stx<<" "<<sty<<endl;
cout<<(stx+edx)<<" "<<sty+edy<<endl;
cout<<edx<<" "<<edy<<endl;
}
else if((abs(d))<=131){
cout<<"3\n";
cout<<stx<<" "<<sty<<endl;
if(d>0){
double nowx=stx-sty,nowy=sty+stx;
cout<<stx-sty<<" "<<sty+stx<<endl;
auto [u,v]=nmb(nowx,nowy,edx,edy);
cout<<u<<" "<<v<<endl;
}
else{
double nowx=stx+sty,nowy=sty-stx;
cout<<stx+sty<<" "<<sty-stx<<endl;
auto [u,v]=nmb(nowx,nowy,edx,edy);
cout<<u<<" "<<v<<endl;
}
cout<<edx<<" "<<edy<<endl;
}
else{
cout<<"4\n";
cout<<stx<<" "<<sty<<endl;
if(d>0){
double nowx=-sty,nowy=stx;
cout<<stx-sty<<" "<<sty+stx<<endl;
cout<<-sty<<" "<<stx<<endl;
cout<<(nowx+edx)<<" "<<nowy+edy<<endl;
}
else{
cout<<stx+sty<<" "<<sty-stx<<endl;
cout<<sty<<" "<<-stx<<endl;
double nowx=sty,nowy=-stx;
//cout<<"???"<<nowx<<" "<<nowy<<endl;
cout<<(nowx+edx)<<" "<<nowy+edy<<endl;
}
cout<<edx<<" "<<edy<<endl;
}
}
signed main(){
init();
ios_base::sync_with_stdio(false), cin.tie(0);
cout<<fixed<<setprecision(12);
int t=1;
cin>>t;
while(t--){
solve();
}
return 0;
}
L.Candy Machine
Topic analysis
Given a sequence , You can choose one interval at a time , The weight of the interval is defined as the number of numbers strictly greater than the average of the interval , Find the maximum interval weight .
Sort the input sequence and expand the interval left , Take the maximum number of binary digits .
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e6 + 10;
int a[N];
inline void solve(){
int n = 0, sum = 0, ans = 0; cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
sort(a + 1, a + 1 + n);
for(int i = 1; i <= n; i++){
sum += a[i];
int l = 1, r = i;
while(l <= r){
int mid = l + r >> 1;
if(a[mid] * i > sum) r = mid - 1;
else l = mid + 1;
}
ans = max(ans, i - r);
}
cout << ans << endl;
}
signed main(){
ios_base::sync_with_stdio(false);
solve();
return 0;
}
M.BpbBppbpBB
Topic analysis
It is required to find according to the given shape B And Glyph P The font , Ensure that there is no overlap .
The scope of discovery is very small , So consider first O ( n 2 ) O(n^2) O(n2) Violent enumeration finds out the number of circles , Set to c n t _ w cnt\_w cnt_w, find ′ # ′ '\#' ′#′ The number of , Set to c n t _ b cnt\_b cnt_b;
Then set the answer as x x x individual B The font , y y y individual P The font , You can list the equations :
146 x + 100 y = c n t _ b 2 x + y = c n t _ w 146x + 100y = cnt\_b \\ 2x + y = cnt\_w 146x+100y=cnt_b2x+y=cnt_w
Then solve the equation .
Code
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N = 1e3 + 10;
int n, m;
char g[N][N];
char sm[7][10] = {
"######",
"##..##",
"#....#",
"#....#",
"##..##",
"######"
};
inline bool dfs(int x, int y){
for(int i = 0; i < 6; i++){
for(int j = 0; j < 6; j++){
if(g[x + i][y + j] != sm[i][j]) return false;
}
}
return true;
}
inline void solve(){
cin >> n >> m;
int cnt_b = 0, cnt_w = 0;
for(int i = 1; i <= n; i++) cin >> g[i] + 1;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(g[i][j] == '#') cnt_b++;
if(dfs(i, j)) cnt_w++;
}
}
cout << (100 * cnt_w - cnt_b) / 54 << " " << (cnt_b - (73 * cnt_w)) / 27;
}
signed main(){
ios_base::sync_with_stdio(false), cin.tie(0);
solve();
return 0;
}
边栏推荐
猜你喜欢
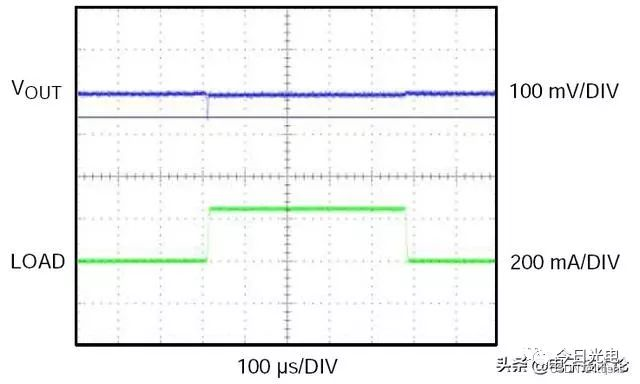
LDO voltage stabilizing chip - internal block diagram and selection parameters
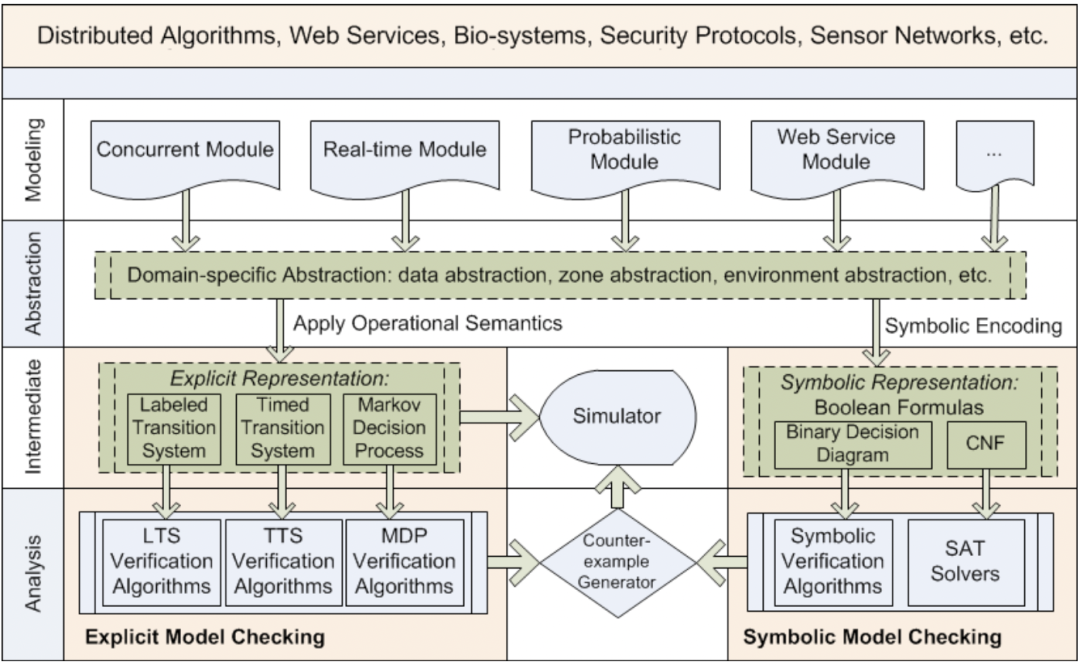
In the field of software engineering, we have been doing scientific research for ten years!
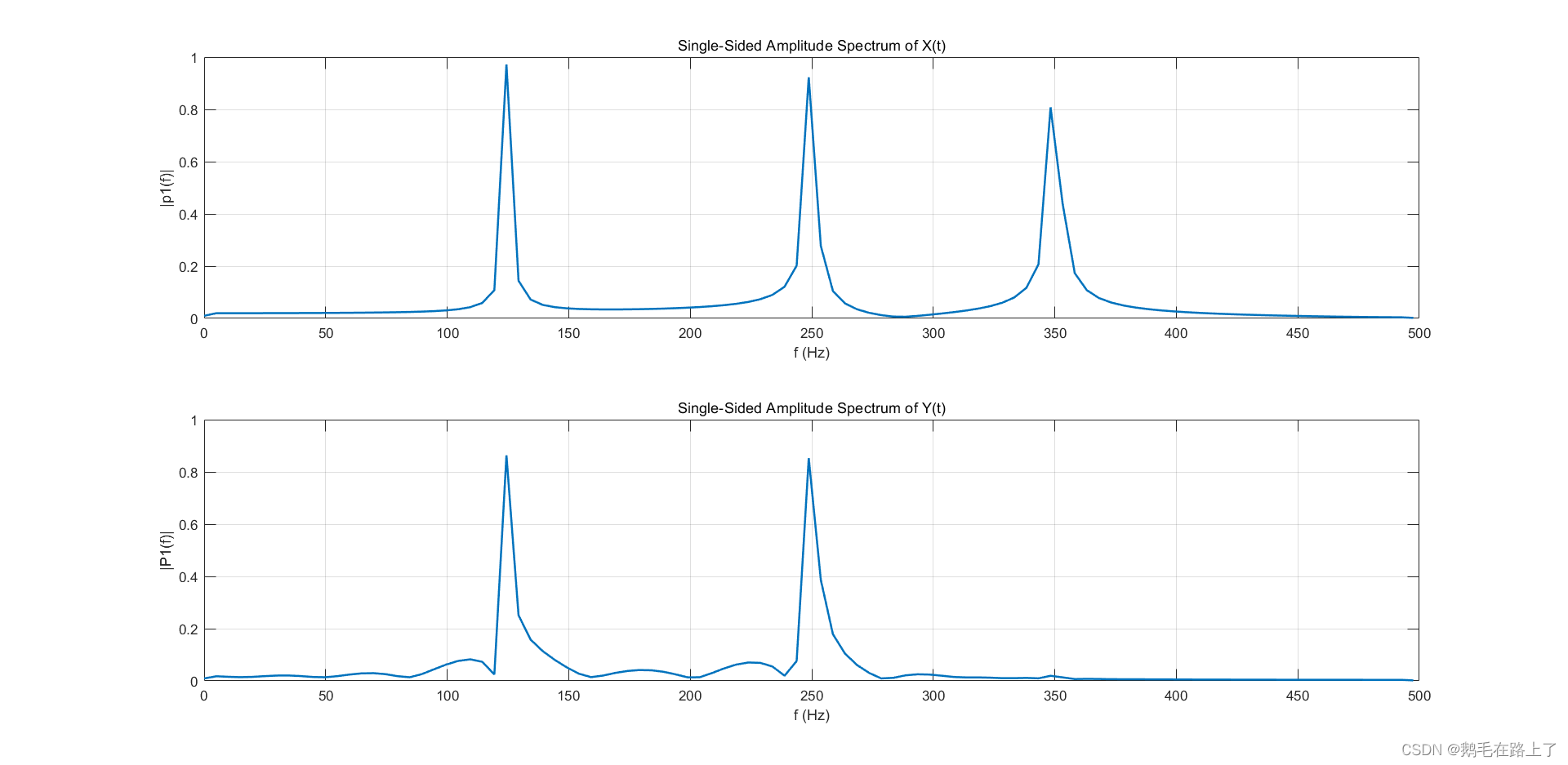
Matlab 信号处理【问答随笔·2】
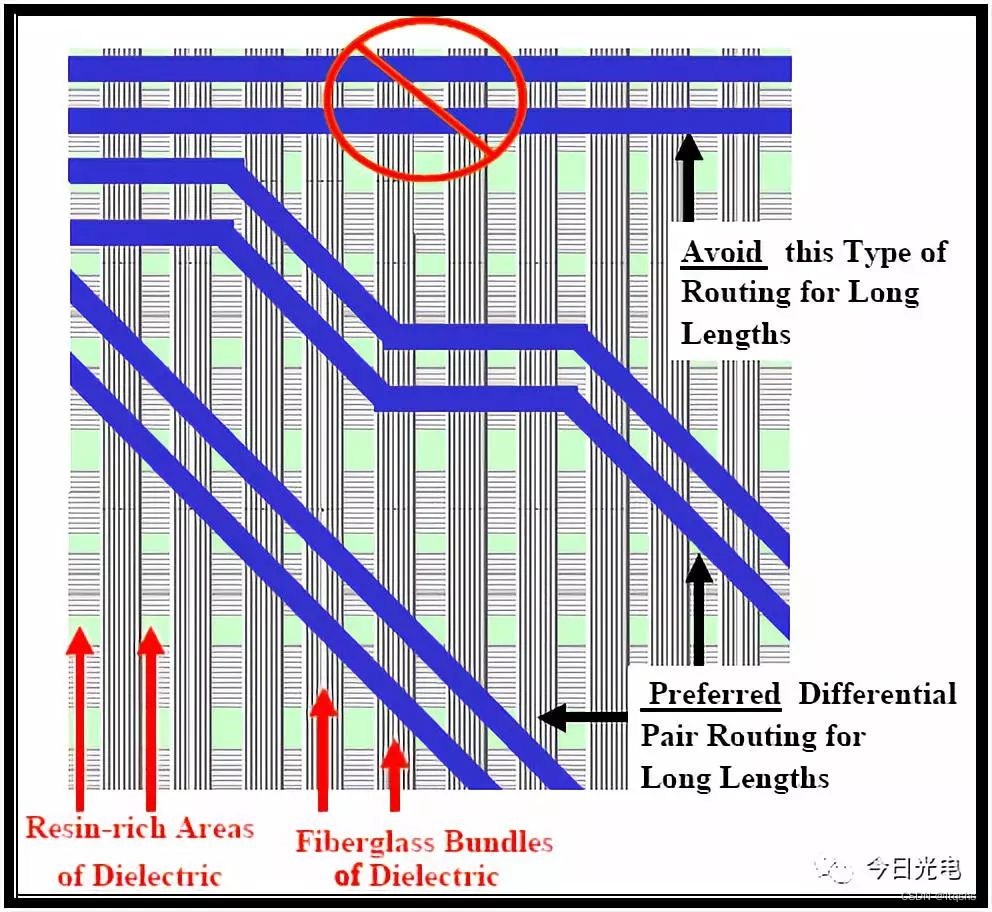
PCI-Express接口的PCB布线规则

成年人只有一份主业是要付出代价的,被人事劝退后,我哭了一整晚

Adults have only one main job, but they have to pay a price. I was persuaded to step back by personnel, and I cried all night
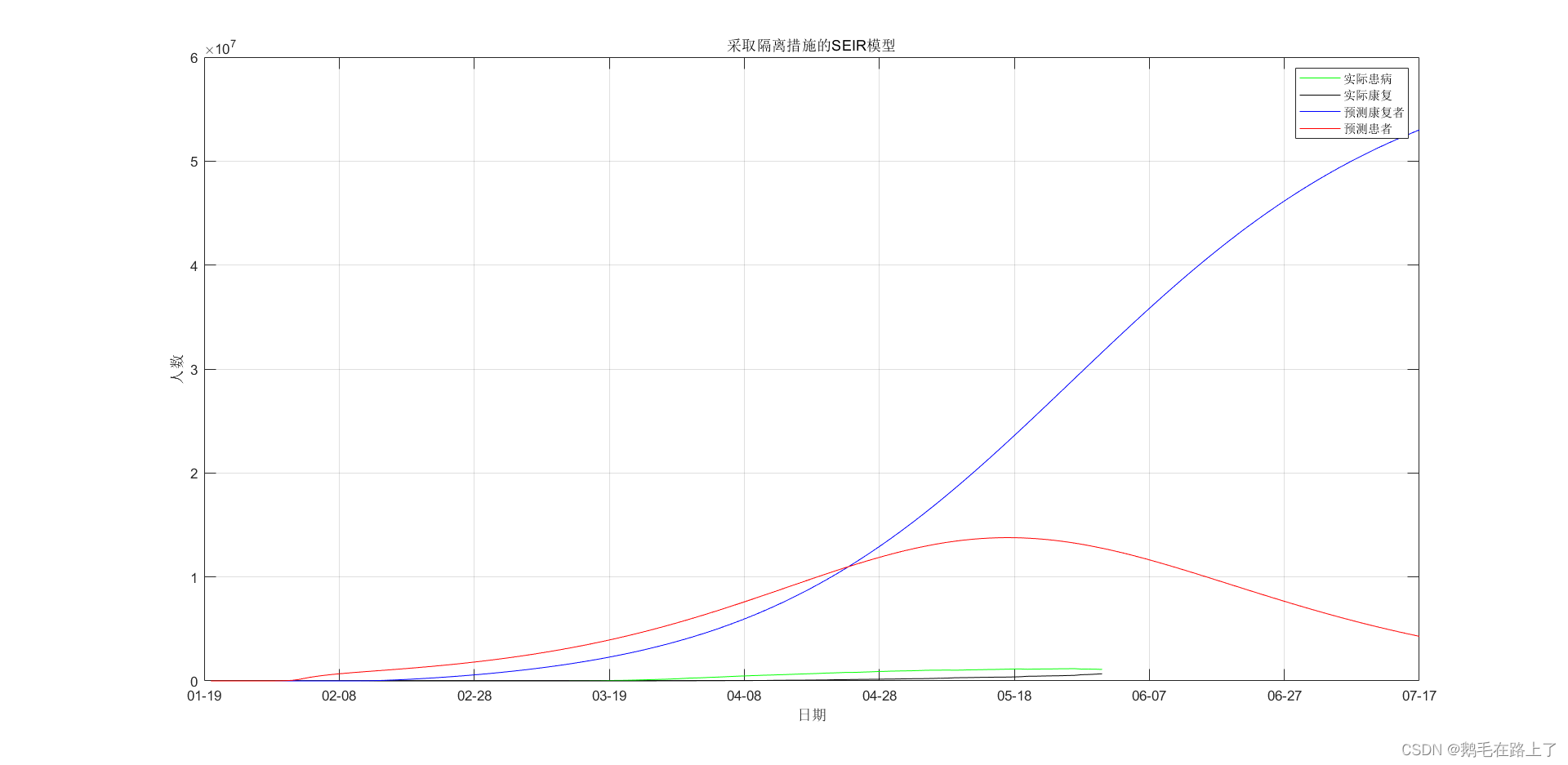
Matlab-SEIR传染病模型预测

STL标准模板库(Standard Template Library)一周学习总结
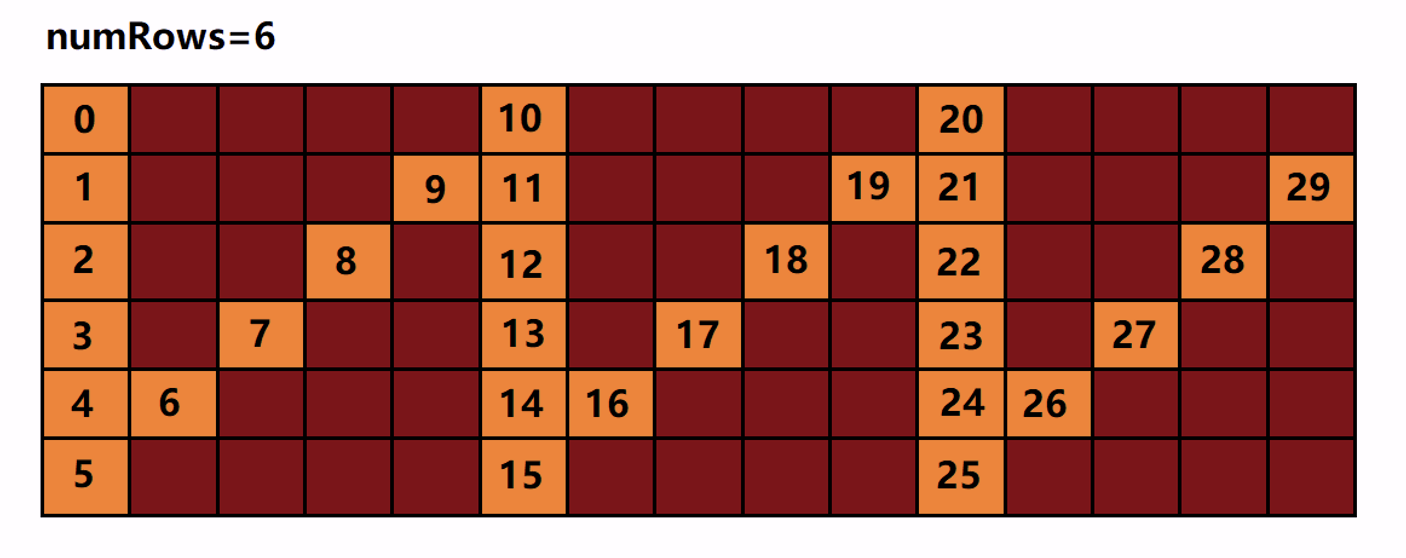
LeeCode -- 6. Z 字形变换
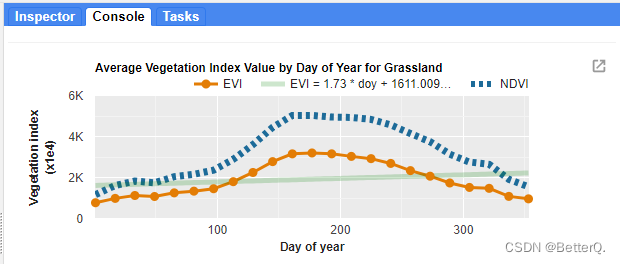
GEE(四):计算两个变量(影像)之间的相关性并绘制散点图
随机推荐
Unity3D学习笔记5——创建子Mesh
USB (十七)2022-04-15
Gee (III): calculate the correlation coefficient between two bands and the corresponding p value
USB(十五)2022-04-14
树后台数据存储(採用webmethod)[通俗易懂]
Install Fedora under RedHat
深入理解Mysql锁与事务隔离级别
LDO voltage stabilizing chip - internal block diagram and selection parameters
2021ICPC上海 H.Life is a Game Kruskal重构树
js 获取对象的key和value
Talk about the design and implementation logic of payment process
14、 Two methods of database export and import
leetcode-520. Detect capital letters -js
网络安全-sqlmap与DVWA爆破
USB(十四)2022-04-12
Network security - Eternal Blue
LDO稳压芯片-内部框图及选型参数
Wechat forum exchange applet system graduation design (3) background function
聊聊支付流程的设计与实现逻辑
Specific method example of V20 frequency converter manual automatic switching (local remote switching)