当前位置:网站首页>【编译原理】词法分析设计实现
【编译原理】词法分析设计实现
2022-07-07 21:50:00 【RemainsHll】
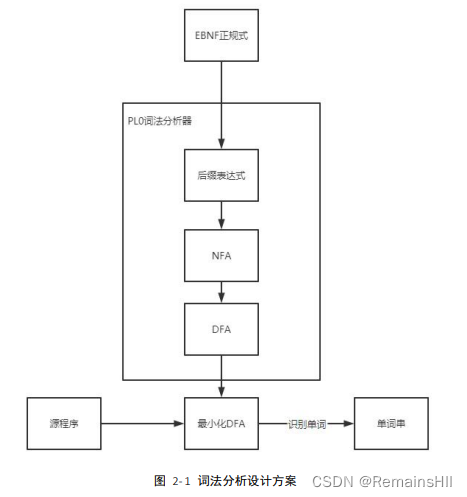
1总体设计
2中缀表达式转后缀表达式
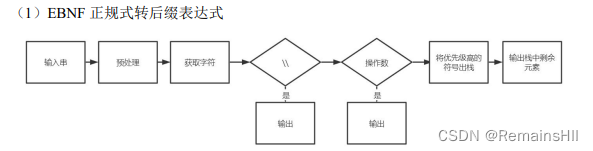
核心代码
int priority(char ch)
{
if (ch == '*')
{
return 3;
}
if (ch == '&')
{
return 2;
}
if (ch == '|')
{
return 1;
}
if (ch == '(')
{
return 0;
}
}
void insert_behind_n(string& s, int n, char ch)
{
s += '#';
for (int i = s.size() - 1; i > n; i--)
s[i] = s[i - 1];
s[n] = ch;
}
void pre_process(string& s)
{
int i = 0, length = s.size()-1;
while (i < length)
{
int in_all_1 = 0, in_all_2 = 0;
//注意转义
if(operators.count(s[i])==0 && s[i]!='\\'){
in_all_1 = 1;
}
if(operators.count(s[i+1])==0 ){
in_all_2 = 1;
}
if (in_all_1 || (s[i] == '*') || (s[i] == ')')){
if (in_all_2 || s[i + 1] == '(')
{
insert_behind_n(s, i + 1, '&');
length++;
}
}
i++;
}
}
string infix_Suffix(string s)
{
pre_process(s);
string str;
stack<char> oper;
for (unsigned int i = 0; i < s.size(); i++)
{
int in_all = 0;
if(s[i] == '\\'){
str += s[i];
i++;
str += s[i];
operands.insert(s[i]);
}
if(operators.count(s[i])==0){
in_all = 1;
operands.insert(s[i]);
}
if (in_all)
{
str += s[i];
}
else
{
if (s[i] == '(')
{
oper.push(s[i]);
}
else if (s[i] == ')')
{
char ch = oper.top();
while (ch != '(')
{
str += ch;
oper.pop();
ch = oper.top();
}
oper.pop();
}
else
{
if (!oper.empty())
{
char ch = oper.top();
while (priority(ch) >= priority(s[i]))
{
str += ch;
oper.pop();
if (oper.empty())
{
break;
}
else ch = oper.top();
}
oper.push(s[i]);
}
else
{
oper.push(s[i]);
}
}
}
}
while (!oper.empty())
{
char ch = oper.top();
oper.pop();
str += ch;
}
//cout<<str<<endl;
return str;
}
3后缀表达式转NFA
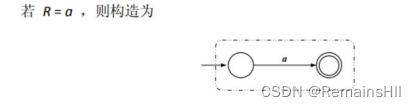
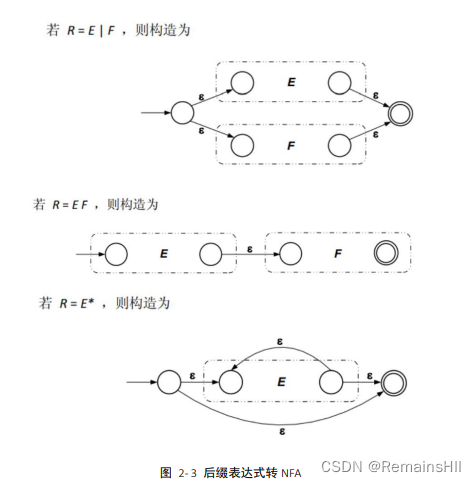
核心代码
//DFA的状态栈,记录起始状态和终结状态
State stateStack[MAX];
int top;
//获取ID
int stateID = 1;
void CFG_NFA(string cfg){
stateID = 1;
top = 0;
point = 0;
for (int i=0;i<cfg.length();i++){
State a;
State b;
State c;
switch (cfg[i])
{
case '&':
//从状态栈中取出两个状态,并更新起始和终结状态
a = stateStack[top--];
b = stateStack[top--];
c.begin = b.begin;
c.end = a.end;
stateStack[++top] = c;
//新建一个状态转移,a状态遇到#转移到b,将a和b状态连接起来
NFA nfa0;
nfa0.from = b.end;
nfa0.to = a.begin;
nfa0.c = '#';
nfa[point++] = nfa0;
break;
case '|':
//规则2
c.begin = stateID++;
c.end = stateID++;
a = stateStack[top--];
b = stateStack[top--];
stateStack[++top] = c;
NFA nfa1;
nfa1.from = c.begin;
nfa1.to = a.begin;
nfa1.c = '#';
nfa[point++] = nfa1;
NFA nfa2;
nfa2.from = c.begin;
nfa2.to = b.begin;
nfa2.c = '#';
nfa[point++] = nfa2;
NFA nfa3;
nfa3.from = a.end;
nfa3.to = c.end;
nfa3.c = '#';
nfa[point++] = nfa3;
NFA nfa4;
nfa4.from = b.end;
nfa4.to = c.end;
nfa4.c = '#';
nfa[point++] = nfa4;
break;
case '*':
//规则3
c.begin = stateID++;
c.end = stateID++;
a = stateStack[top--];
stateStack[++top] = c;
NFA nfa5;
nfa5.from = c.begin;
nfa5.to = c.end;
nfa5.c = '#';
nfa[point++] = nfa5;
NFA nfa6;
nfa6.from = c.begin;
nfa6.to = a.begin;
nfa6.c = '#';
nfa[point++] = nfa6;
NFA nfa7;
nfa7.from = a.end;
nfa7.to = a.begin;
nfa7.c = '#';
nfa[point++] = nfa7;
NFA nfa8;
nfa8.from = a.end;
nfa8.to = c.end;
nfa8.c = '#';
nfa[point++] = nfa8;
break;
case '\\':
//遇到转义字符
i++;
c.begin = stateID++;
c.end = stateID++;
stateStack[++top] = c;
NFA nfa10;
nfa10.from = c.begin;
nfa10.to = c.end;
nfa10.c = cfg[i];
nfa[point++] = nfa10;
break;
default:
//遇到操作数
c.begin = stateID++;
c.end = stateID++;
stateStack[++top] = c;
NFA nfa9;
nfa9.from = c.begin;
nfa9.to = c.end;
nfa9.c = cfg[i];
nfa[point++] = nfa9;
break;
}
}
//输出NFA
// for(int i=0;i<point;i++){
// cout<<nfa[i].from<<" "<<nfa[i].c<<" "<<nfa[i].to<<endl;
// }
}
4NFA转DFA
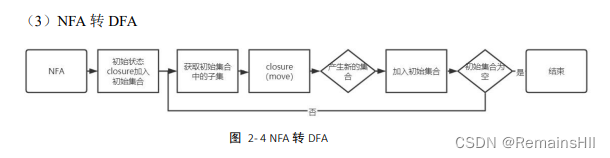
核心代码
set<int> empty_transfer(int id){
set<int> set1;
set<int> set2;
set1.insert(id);
//遍历NFA,将到达的状态集合加入set1和set2
for(int i=0;i<point;i++){
if(nfa[i].from==id && nfa[i].c == '#'){
set1.insert(nfa[i].to);
set2.insert(nfa[i].to);
}
}
//遍历上述得到的set2,继续求空转移,直到set2为空,得到的set1就是状态的空转移
while(!set2.empty()){
int temp = *set2.begin();
set2.erase(set2.begin());
for(int i=0;i<point;i++){
if(nfa[i].from==temp && nfa[i].c == '#'){
set2.insert(nfa[i].to);
set1.insert(nfa[i].to);
}
}
}
return set1;
}
set<int> empty_move(int id,char c){
//先求move(c)
set<int> set1;
for(int i=0;i<point;i++){
if(nfa[i].from==id && nfa[i].c == c){
set1.insert(nfa[i].to);
}
}
//得到move之后求空转移
set<int> set2;
set2.insert(set1.begin(),set1.end());
set<int>::iterator it1;
for (it1 = set1.begin(); it1 != set1.end(); it1++){
set<int> set3 = empty_transfer(*it1);
set2.insert(set3.begin(),set3.end());
}
return set2;
}
void NFA_DFA(){
DFA* dfa = new DFA();
//获取开始状态和终结状态
State ss = stateStack[top];
int begin = ss.begin;
int end = ss.end;
//初始状态的空转移
set<int> initial = empty_transfer(begin);
//状态集合
set< set<int> > states;
set< set<int> > states_temp;
states.insert(initial);
//重命名DFA
dfa->dfa_id[initial] = ++dfa->id;
//遍历状态集合
while(!states.empty()){
set<int> temp = *states.begin();
states.erase(states.begin());
set<int>::iterator it1;
set<char>::iterator it2;
//遍历操作数求closeuure(move)
for (it2 = operands.begin(); it2 != operands.end(); it2++){
set<int> new_set;
for (it1 = temp.begin(); it1 != temp.end(); it1++){
set<int> set_temp = empty_move(*it1,*it2);
new_set.insert(set_temp.begin(),set_temp.end());
}
if(states_temp.count(new_set) == 0 && !new_set.empty()){
states.insert(new_set);
states_temp.insert(new_set);
dfa->dfa_id[new_set] = ++dfa->id;
}
//cout<<dfa->dfa_id[temp]<<" "<<*it2<<" "<<dfa->dfa_id[new_set]<<endl;
dfa->tran[dfa->dfa_id[temp]][*it2-33] = dfa->dfa_id[new_set];
if(new_set.count(end)){
dfa->vn[dfa->dfa_id[new_set]] = true;
}else{
dfa->vn[dfa->dfa_id[new_set]] = false;
}
}
}
dfas[point_dfa++] = dfa;
}
5最小化DFA
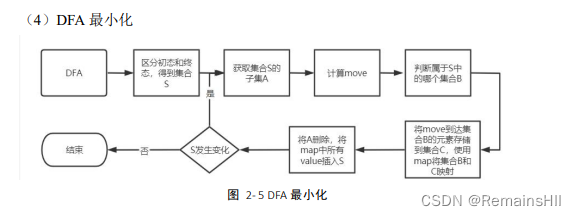
核心代码
void minimize_DFA(){
set<set<int> > sets;
DFA* dfa = dfas[point_dfa-1];
//初始化:初态和终态区分
int len = dfa->id;
set<int> set1,set2;
for(int i=1;i<=len;i++){
if(dfa->vn[i]){
set1.insert(i);
}else{
set2.insert(i);
}
}
sets.insert(set1);
sets.insert(set2);
set<set<int> > begin_set;
do{
begin_set = sets;
set<set<int> >::iterator it1;
set<int> temp;
//遍历状态集合
for (it1 = begin_set.begin(); it1 != begin_set.end(); it1++){
temp= *it1;
set<char>::iterator it2;
//遍历操作数
for(it2 = operands.begin();it2 != operands.end();it2++){
map<set<int>,set<int> > map_set;
set<int>::iterator it3;
for(it3 = temp.begin();it3 != temp.end();it3++){
int d = dfa->tran[*it3][*it2-33];
//判断属于哪个集合
//cout<<*it3<<" "<<*it2<<" "<<d<<endl;
set<set<int> >::iterator it4;
int flag = 0;
set<int>temp2,temp3;
for(it4 = begin_set.begin();it4 != begin_set.end();it4++){
temp2 = *it4;
if(temp2.count(d)>0){
temp3 = map_set[temp2];
flag = 1;
}
}
//如果状态产生了新的状态集合, 即可以分割,将原来的状态删除,状态集合存入到map中。
if(flag == 1){
sets.erase(temp);
temp3.insert(*it3);
map_set[temp2] = temp3;
}
}
//将map中的集合插入到原集合中
map<set<int>,set<int> >::iterator it5;
for(it5 = map_set.begin();it5 != map_set.end();it5++){
sets.insert(it5->second);
}
}
}
}while(begin_set != sets);
//将最小化的DFA重命名。
DFA* min_dfa = new DFA();
set<set<int> >::iterator it6;
set<set<int> > sets_temp;
//遍历最小化DFA得到的集合
for(it6 = sets.begin();it6 != sets.end();it6++){
set<int> t_set = *it6;
set<char>::iterator it7;
int f = *t_set.begin();
int id=0,to=0;
//新建DFA状态
if(sets_temp.count(t_set) == 0){
sets_temp.insert(t_set);
min_dfa->dfa_id[t_set] = ++min_dfa->id;
}
id = min_dfa->dfa_id[t_set];
//编译操作符,得到状态转移矩阵和终结符数组
for(it7 = operands.begin();it7 != operands.end();it7++){
to = 0;
int d = dfa->tran[f][*it7 -33];
set<set<int> >::iterator it8;
for(it8 = sets.begin();it8 != sets.end();it8++){
set<int> t_set2 = *it8;
if(t_set2.count(d)>0){
if(sets_temp.count(t_set2) == 0){
min_dfa->dfa_id[t_set2] = ++min_dfa->id;
sets_temp.insert(t_set2);
}
to = min_dfa->dfa_id[t_set2];
if(min_dfa->vn[d]){
min_dfa->vn[to] = true;
}
}
}
min_dfa->tran[id][*it7-33] = d;
}
}
dfas[point_dfa] = min_dfa;
}
6识别单词
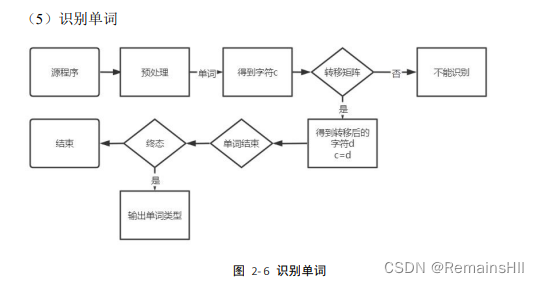
核心代码
int distinguish(string s){
for(int i = 0;i<point_dfa;i++){
int cur = 1,flag = 1;
DFA* dfa = dfas[i];
int to = 0;
//一直转移,知道单词结束
for(int j = 0;j<s.length();j++){
to = dfa->tran[cur][s[j]-33];
if(to == 0){
flag = 0;
}else{
cur = to;
}
}
//如果单词能完成全部状态转移,并且转移到的状态为终态,将DFA的id返回。
if(flag ==1 && dfa->vn[to]){
return i;
}
}
return -1;
}
7测试结果

边栏推荐
- 网络安全-CSRF
- Wechat forum exchange applet system graduation design completion (4) opening report
- What is ADC sampling rate (Hz) and how to calculate it
- Circumvention Technology: Registry
- Understand the session, cookie and token at one time, and the interview questions are all finalized
- Network security - joint query injection
- Online interview, how to better express yourself? In this way, the passing rate will be increased by 50%~
- 微信论坛交流小程序系统毕业设计毕设(8)毕业设计论文模板
- 十四、数据库的导出和导入的两种方法
- Unity dynamically merges mesh textures
猜你喜欢

PMP项目管理考试过关口诀-1

Wechat forum exchange applet system graduation design completion (6) opening defense ppt
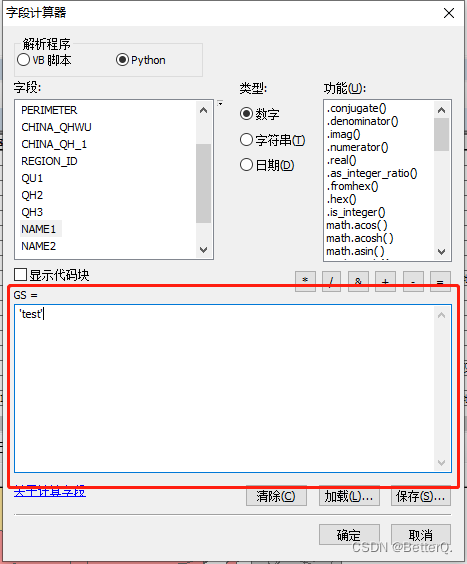
ArcGIS:字段赋值_属性表字段计算器(Field Calculator)依据条件为字段赋值
【微服务|SCG】gateway整合sentinel

微信论坛交流小程序系统毕业设计毕设(7)中期检查报告
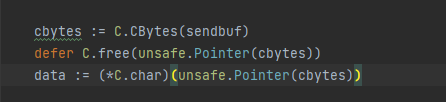
Develop those things: go plus c.free to free memory, and what are the reasons for compilation errors?

iNFTnews | NFT技术的广泛应用及其存在的问题
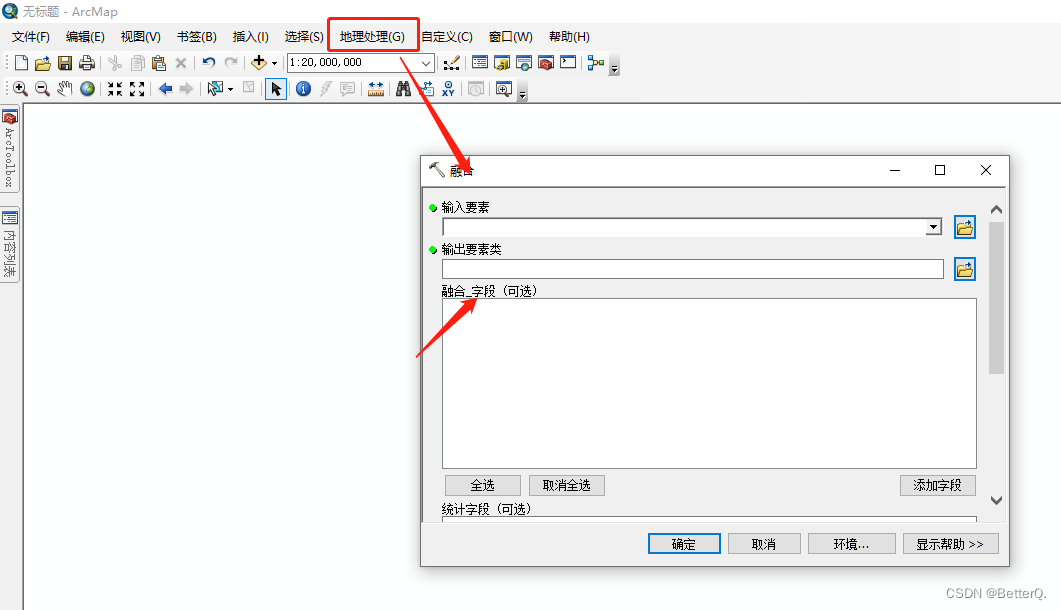
ArcGIS: two methods of attribute fusion of the same field of vector elements
U盘拷贝东西时,报错卷错误,请运行chkdsk

DTC社群运营怎么做?
随机推荐
微信论坛交流小程序系统毕业设计毕设(2)小程序功能
Adrnoid开发系列(二十五):使用AlertDialog创建各种类型的对话框
./ setup. Insufficient sh permission
Unity and webgl love each other
Wechat forum exchange applet system graduation design completion (6) opening defense ppt
Years of summary, some core suggestions for learning programming
[record of question brushing] 3 Longest substring without duplicate characters
Are the microorganisms in the intestines the same as those on the skin?
小程序多种开发方式对比-跨端?低代码?原生?还是云开发?
Classification and prediction of heartbeat signal
Exploratory data analysis of heartbeat signal
Unity 动态合并网格纹理
Wechat forum exchange applet system graduation design completion (8) graduation design thesis template
Why does the market need low code?
微生物健康網,如何恢複微生物群落
Use JfreeChart to generate curves, histograms, pie charts, and distribution charts and display them to jsp-2
Handling file exceptions
Wechat forum exchange applet system graduation design (2) applet function
DTC社群运营怎么做?
Software evaluation center ▏ what are the basic processes and precautions for automated testing?