[21-Day Learning Challenge] A small summary of sequential search and binary search

​
​

活动地址：CSDN21天学习挑战赛

顺序查找

What is a sequential search

Sequential search is often used in our life
For example, we want to find a card in a pile of playing cards,
How do we find it
The easiest way is to find them one by one
This is the principle of sequential search
Sequential search is to traverse the array from the beginning to the end,Find the desired number

代码

for(int i=0;i<arr.length;i++){
    
	if(arr[i]==target){
    
		return i;
	}
}

时间复杂度

Because the worst case is to traverse the array,
因此时间复杂度为O(n)

*二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1.

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/binary-search
著作权归领扣网络所有.商业转载请联系官方授权,非商业转载请注明出处.

什么是二分查找

以升序数列为例,比较一个元素与数列中的中间位置的元素的大小,如果比中间位置的元素大,则继续在后半部分的数列中进行二分查找;如果比中间位置的元素小,则在数列的前半部分进行比较;如果相等,则找到了元素的位置.每次比较的数列长度都会是之前数列的一半,直到找到相等元素的位置或者最终没有找到要找的元素.
简单来说,Just look for the big ones to the right,If you see a small one, look left

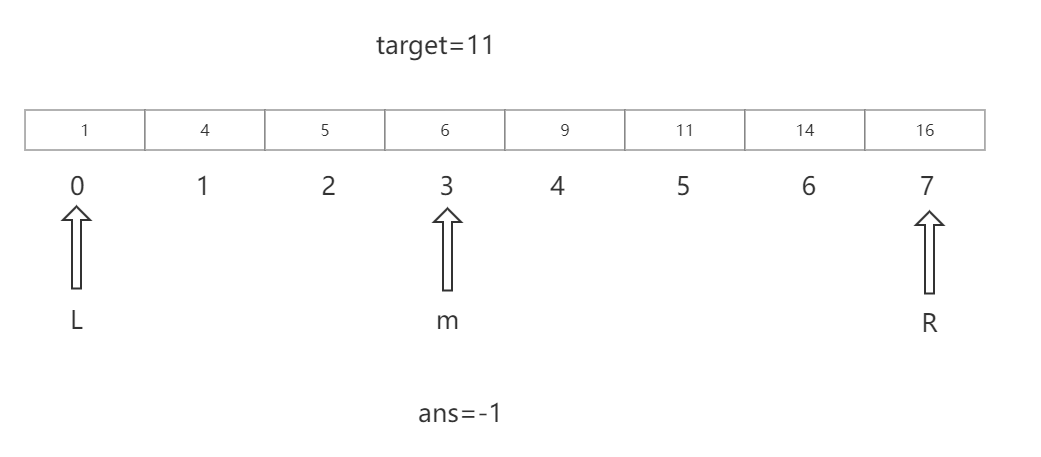
nums[m]<target,So look on the right

nums[m]==target,ans=5

代码

class Solution {
    
    public int search(int[] nums, int target) {
    
        int n=nums.length;
        int l=0;
        int r=n-1;
        while(l<=r){
    
            int m=l+(r-l)/2;
            if(nums[m]<target){
    
                l=m+1;
            }else if(nums[m]>target){
    
                r=m-1;
            }else{
    
                return m;
            }
        }
        return -1;    
    }
}

进阶:在一个有序数组中,找>=某个数最左侧的位置

一直二分到死

代码

	public static int nearestIndex(int[] arr, int value) {
    
		int L = 0;
		int R = arr.length - 1;
		int index = -1; // 记录最左的对号
		while (L <= R) {
     // 至少一个数的时候
			int mid = L + ((R - L) >> 1);
			if (arr[mid] >= value) {
    
				index = mid;
				R = mid - 1;
			} else {
    
				L = mid + 1;
			}
		}
		return index;
	}

同理,在一个有序数组中,找<=某个数最右侧的位置,It's the same solution

	public static int nearestIndex(int[] arr, int value) {
    
		int L = 0;
		int R = arr.length - 1;
		int index = -1; // 记录最右的对号
		while (L <= R) {
    
			int mid = L + ((R - L) >> 1);
			if (arr[mid] <= value) {
    
				index = mid;
				L = mid + 1;
			} else {
    
				R = mid - 1;
			}
		}
		return index;
	}

进阶2:局部最小值问题

在一个无序数组中, The value may be positive, 负, 或者零, Any two adjacent numbers in an array must not be equal.
Define a local minimum:
1.长度为1,arr[0]就是局部最小;
2.数组的开头,如果arr[0] < arr[1] ,arr[0]is defined as a local minimum.
3.数组的结尾,如果arr[N-1] < arr[N-2] ,arr[N-1]is defined as a local minimum.
any intermediate positioni, 即数组下标1~N-2之间, 必须满足arr[i-1] < arr[i] <arr[i+1] ,is called finding a local minimum.
Find any local minimum and return it.

解题思路

先单独看0位置和n-1位置,If neither side is a local minimum,Then if you connect each number of the array on the coordinate axis,There must be a local minimum position,从中间分开,If the middle position is not a local minimum,It doesn't matter which half it is,There are also local minima,Something like this builds something like exclusivity,two points,

代码

	public static int getLessIndex(int[] arr) {
    
		if (arr == null || arr.length == 0) {
    
			return -1;
		}
		if (arr.length == 1 || arr[0] < arr[1]) {
    
			return 0;
		}
		if (arr[arr.length - 1] < arr[arr.length - 2]) {
    
			return arr.length - 1;
		}
		int left = 1;
		int right = arr.length - 2;
		int mid = 0;
		while (left < right) {
    
			mid = (left + right) / 2;
			if (arr[mid] > arr[mid - 1]) {
    
				right = mid - 1;
			} else if (arr[mid] > arr[mid + 1]) {
    
				left = mid + 1;
			} else {
    
				return mid;
			}
		}
		return left;
	}

二分总结

1)数据状况特殊
2)The problem itself is special

Dichotomy does not necessarily require order
Depends what your problem is,Depends on what your data status is
As long as you can build something exclusive, There must be half on the left and right sides,The other half may not
If you are only looking for one,Just cut in half, As long as you can build something like exclusivity, You get two points,不一定要求数组有序