当前位置:网站首页>[combinatorics] generating function (use generating function to solve the number of solutions of indefinite equation)
[combinatorics] generating function (use generating function to solve the number of solutions of indefinite equation)
2022-07-03 18:00:00 【Programmer community】
List of articles
- One 、 Use generating function to solve the number of solutions of indefinite equation
- 1、 With restrictions
- 2、 With coefficients
Reference blog :
- 【 Combinatorial mathematics 】 Generating function Brief introduction ( Generating function definition | Newton's binomial coefficient | Common generating functions | Related to constants | Related to binomial coefficient | Related to polynomial coefficients )
- 【 Combinatorial mathematics 】 Generating function ( Linear properties | Product properties )
- 【 Combinatorial mathematics 】 Generating function ( Shift property )
- 【 Combinatorial mathematics 】 Generating function ( The nature of summation )
- 【 Combinatorial mathematics 】 Generating function ( Commutative properties | Derivative property | Integral properties )
- 【 Combinatorial mathematics 】 Generating function ( Summary of nature | Important generating functions ) *
- 【 Combinatorial mathematics 】 Generating function ( Generate function examples | Given the general term formula, find the generating function | Given the generating function, find the general term formula )
- 【 Combinatorial mathematics 】 Generating function ( Generate function application scenarios | Solving recursive equations using generating functions )
- 【 Combinatorial mathematics 】 Generating function ( Use the generating function to solve multiple sets r Combinatorial number )
One 、 Use generating function to solve the number of solutions of indefinite equation
The number of solutions of the indefinite equation :
x
1
+
x
2
+
⋯
+
x
k
=
r
x_1 + x_2 + \cdots + x_k = r
x1+x2+⋯+xk=r
x
i
x_i
xi For natural Numbers ;
Previously, by combining the corresponding methods , have already been solved , The number of solutions is
C
(
k
+
r
−
1
,
r
)
C(k + r - 1 , r)
C(k+r−1,r)
Number of solutions of indefinite equation , Refer to : 【 Combinatorial mathematics 】 Permutation and combination ( The combinatorial number of multiple sets | The repetition of all elements is greater than the number of combinations | The combinatorial number of multiple sets deduction 1 Division line derivation | The combinatorial number of multiple sets deduction 2 Derivation of the number of nonnegative integer solutions of indefinite equations ) Two 、 Combination of multiple sets The repetition of all elements is greater than the number of combinations deduction 2 ( Derivation of the number of nonnegative integer solutions of indefinite equations )
In the above case ,
x
i
x_i
xi There is no upper limit on the value of , If
x
i
x_i
xi The value is limited , Such as
x
1
x_1
x1 The value must meet
2
≤
x
1
≤
5
2 \leq x_1 \leq 5
2≤x1≤5 When the conditions , You cannot use the above formula to calculate , Need here Use the generating function to solve ;
1、 With restrictions
x
1
+
x
2
+
⋯
+
x
k
=
r
x_1 + x_2 + \cdots + x_k = r
x1+x2+⋯+xk=r
If
x
i
x_i
xi Values are constrained ,
l
i
≤
x
i
≤
n
i
l_i \leq x_i \leq n_i
li≤xi≤ni , Corresponding Generate function items
y
y
y Power value from
l
i
l_i
li To
n
i
n_i
ni ;
The corresponding generating function item is
y
l
i
+
y
l
i
+
1
+
⋯
+
y
n
i
y^{l_i} + y^{l_i + 1} + \cdots + y^{n_i}
yli+yli+1+⋯+yni
The complete generating function is :
G
(
y
)
=
(
y
l
1
+
y
l
1
+
1
+
⋯
+
y
n
1
)
(
y
l
2
+
y
l
2
+
1
+
⋯
+
y
n
2
)
⋯
(
y
l
k
+
y
l
k
+
1
+
⋯
+
y
n
k
)
G(y) = ( y^{l_1} + y^{l_1+1} + \cdots + y^{n_1} )( y^{l_2} + y^{l_2+1} + \cdots + y^{n_2} ) \cdots ( y^{l_k} + y^{l_k+1} + \cdots + y^{n_k} )
G(y)=(yl1+yl1+1+⋯+yn1)(yl2+yl2+1+⋯+yn2)⋯(ylk+ylk+1+⋯+ynk)
Multiply the result of the above generating function ,
y
r
y^r
yr The coefficient before , It's an indefinite equation The number of solutions ;
2、 With coefficients
p
1
x
1
+
p
2
x
2
+
⋯
+
p
k
x
k
=
r
p_1x_1 + p_2x_2 + \cdots + p_kx_k = r
p1x1+p2x2+⋯+pkxk=r
x
i
∈
N
x_i \in N
xi∈N , Nonnegative integer solution , Yes
x
i
x_i
xi No upper limit ;
Nonnegative integer solutions of functions with coefficients , The basic of generating the item of the function The bottom is
y
p
i
y^{p_i}
ypi , The value range of power is
0
,
1
,
2
,
⋯
0 , 1, 2, \cdots
0,1,2,⋯ ,
Each generated function item is
(
y
p
i
)
0
+
(
y
p
i
)
1
+
(
y
p
i
)
2
+
(
y
p
i
)
3
+
⋯
(y^{p_i})^0 + (y^{p_i})^1 + (y^{p_i})^2 + (y^{p_i})^3 + \cdots
(ypi)0+(ypi)1+(ypi)2+(ypi)3+⋯ ,
The simplified item is
1
+
y
p
i
+
y
2
p
i
+
y
3
p
i
+
⋯
1 +y^{p_i} + y^{2p_i} + y^{3p_i} + \cdots
1+ypi+y2pi+y3pi+⋯
Will all
k
k
k Item multiplication , Is the corresponding generating function :
G
(
y
)
=
(
1
+
y
p
1
+
y
2
p
1
+
y
3
p
1
+
⋯
)
(
1
+
y
p
2
+
y
2
p
2
+
y
3
p
2
+
⋯
)
⋯
(
1
+
y
p
k
+
y
2
p
k
+
y
3
p
k
+
⋯
)
G(y)=(1+y^{p_1} + y^{2p_1} + y^{3p_1 + \cdots})(1+y^{p_2} + y^{2p_2} + y^{3p_2 + \cdots}) \cdots (1+y^{p_k} + y^{2p_k} + y^{3p_k + \cdots})
G(y)=(1+yp1+y2p1+y3p1+⋯)(1+yp2+y2p2+y3p2+⋯)⋯(1+ypk+y2pk+y3pk+⋯)
The number of nonnegative integer solutions of the equation is
y
r
y^r
yr The coefficient before ;
边栏推荐
- c# . Net tool ecosystem
- TCP congestion control details | 3 design space
- 解决Zabbix用snmp监控网络流量不准的问题
- SSL / bio pour OpenSSL Get FD
- How to deploy applications on kubernetes cluster
- Redis core technology and practice - learning notes (IX): slicing cluster
- Write a program to process a list container of string type. Find a special value in the container 9.27: and delete it if found. Rewrite the above procedure with deque container.
- The gbase 8A database does not support the DB2 function value (column_name, 0) cluster syntax
- 1146_ SiCp learning notes_ exponentiation
- Count the number of pixel values in the image
猜你喜欢
On Data Mining

Research on Swift

SQL injection database operation foundation
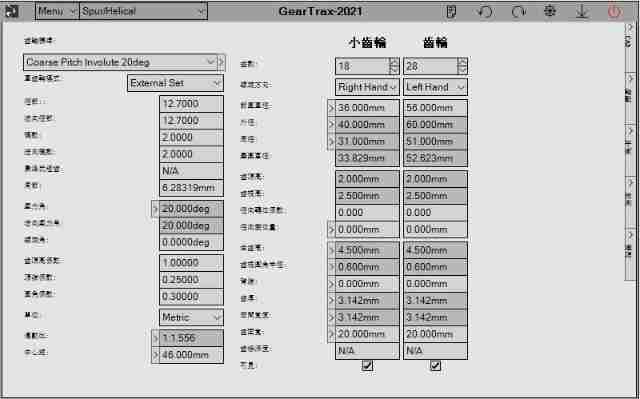
Introduction to SolidWorks gear design software tool geartrax
![网格图中递增路径的数目[dfs逆向路径+记忆dfs]](/img/57/ff494db248171253996dd6c9110715.png)
网格图中递增路径的数目[dfs逆向路径+记忆dfs]

Implementation of Tetris in C language

QT learning diary 9 - dialog box

Global and Chinese health care OEM and ODM market status survey and investment planning recommendations report 2022-2028
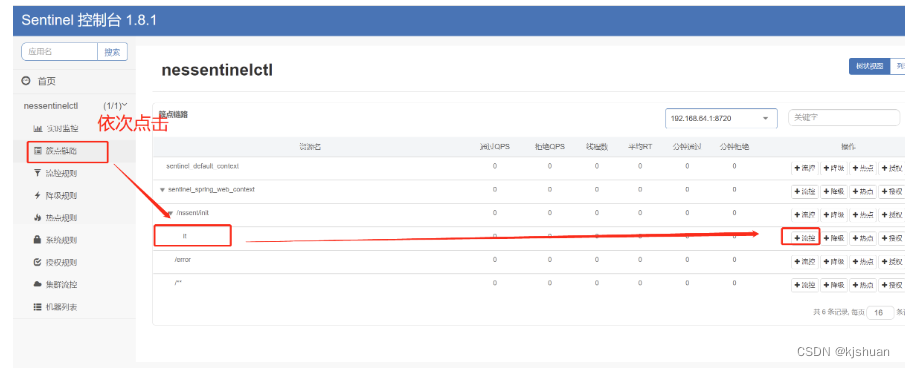
微服务组件Sentinel控制台调用

Ml (machine learning) softmax function to realize the classification of simple movie categories
随机推荐
Inheritance of ES6 class
A. Odd Selection【BruteForce】
Graduation summary
PHP MySQL inserts multiple pieces of data
1146_ SiCp learning notes_ exponentiation
Valentine's day, send you a little red flower~
Introduction to SolidWorks gear design software tool geartrax
PHP MySQL where clause
Micro service component sentinel console call
Postfix tips and troubleshooting commands
Life perception 1
Draw some simple graphics with MFC
[combinatorics] generating function (generating function application scenario | using generating function to solve recursive equation)
Detailed explanation of common network attacks
远程办公工具分享|社区征文
[combinatorics] generating function (property summary | important generating function)*
Leetcode 108 converts an ordered array into a binary search tree -- recursive method
The second largest gay dating website in the world was exposed, and the status of programmers in 2022
Global and Chinese health care OEM and ODM market status survey and investment planning recommendations report 2022-2028
PHP MySQL inserts data