当前位置:网站首页>AVL树的实现
AVL树的实现
2022-07-07 03:10:00 【忱叁】
二叉搜索树
在介绍AVL树之前,大家应该都知道二叉搜索树,实际上AVL树就是在二叉搜索树的基础上改进的.
这张图就是二叉搜索树,我们不难发现,如果左子树的节点都小于根节点,右子树的节点都大于根节点,这就对查询操作是很高效的.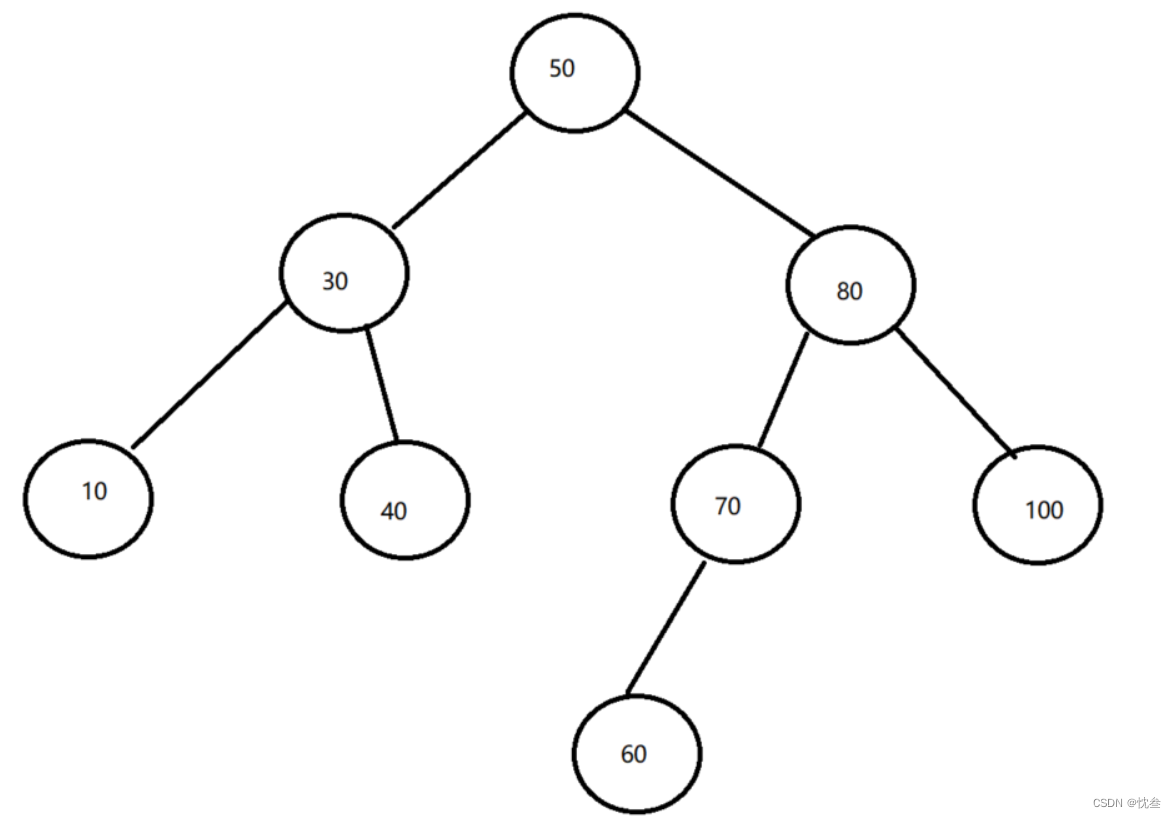
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
采用中序遍历来遍历这个树,就是一个有序的序列(左根右)
分析一下二叉搜索树的时间复杂度
利用二叉搜索树进行查找的时候
时间复杂度是O(logN),但这是最优情况下
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
如果二叉树是正常的树时间复杂度没变,但是要是一颗单分支的树,就不一样了
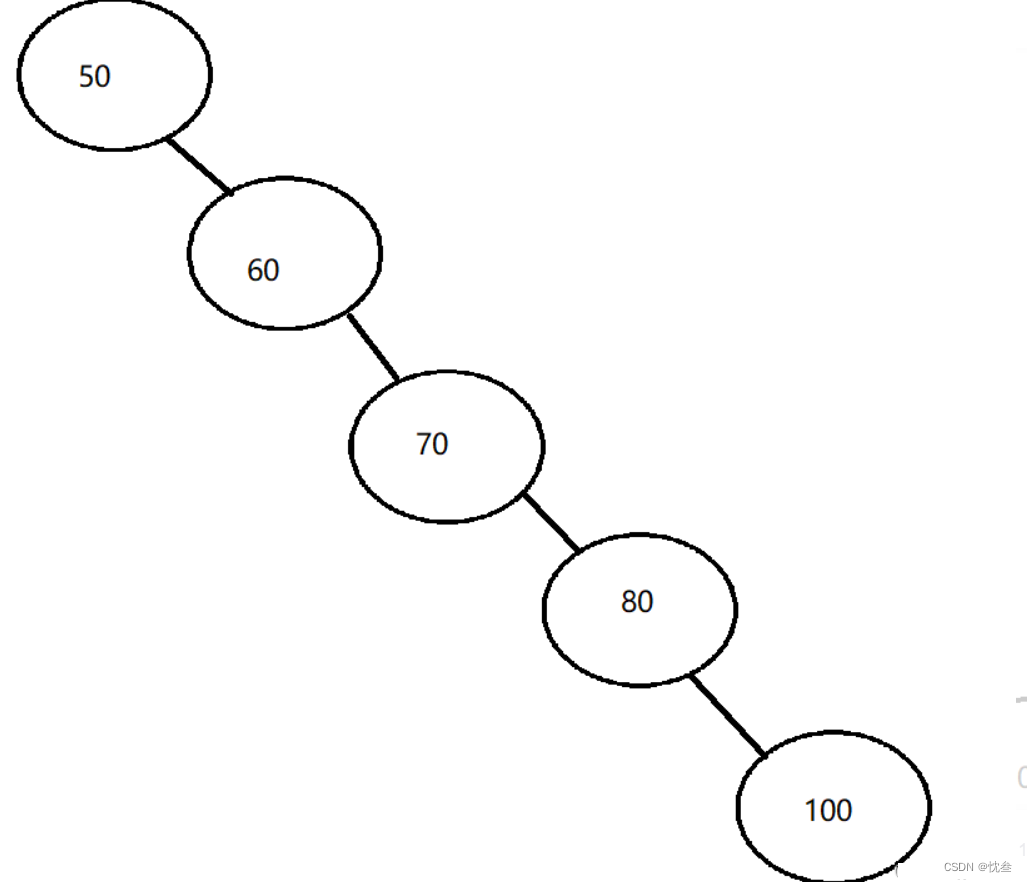
平均比较次数是: N/2
最优情况下的平均比较次数是 log2N
所以二叉搜索树的改进就是要在原基础上避免新插入节点后变成单分支或者类似于单分支的树,
究竟到什么程度才不算类似于单分支的树,就是做出一个限制
限制: 当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
AVL树概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下
因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年 发明了一种解决上述问题的方法:
当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度。
一棵AVL树或者是空树,或者是具有以下性质的二叉搜索树:
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)
在这里我们假设
平衡因子 = 右子树高度 - 左子树高度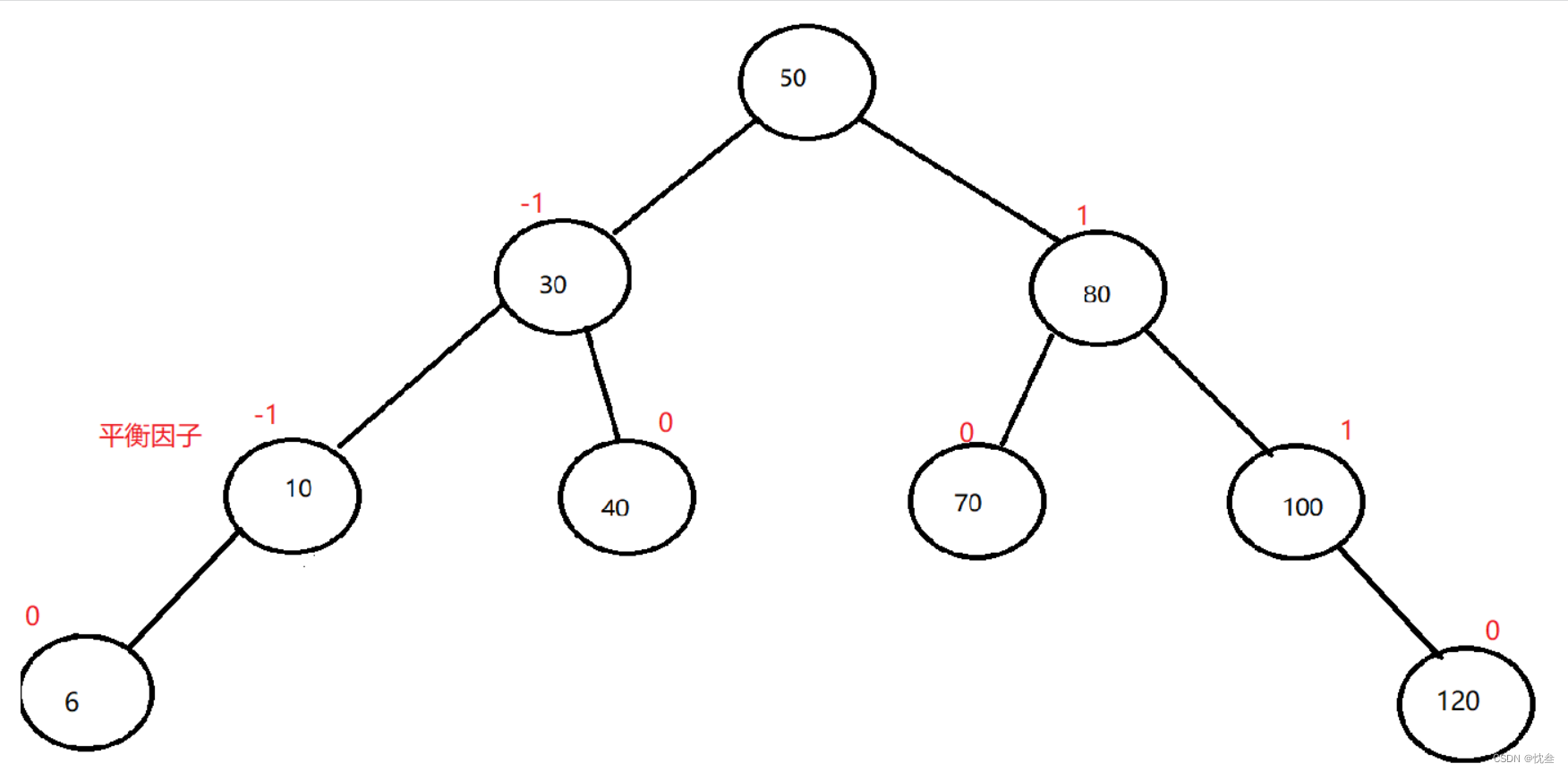
每个节点都有平衡因子,一旦某个节点的平衡因子的值超出范围就不是AVL树,这个时候应该要进行调整,就像大小堆一样,在插入的过程中保证是大小堆,就需要进行向下调整之类的操作.
AVL树的插入
实际上AVL树的插入就很麻烦,在二叉搜索树的基础上进行插入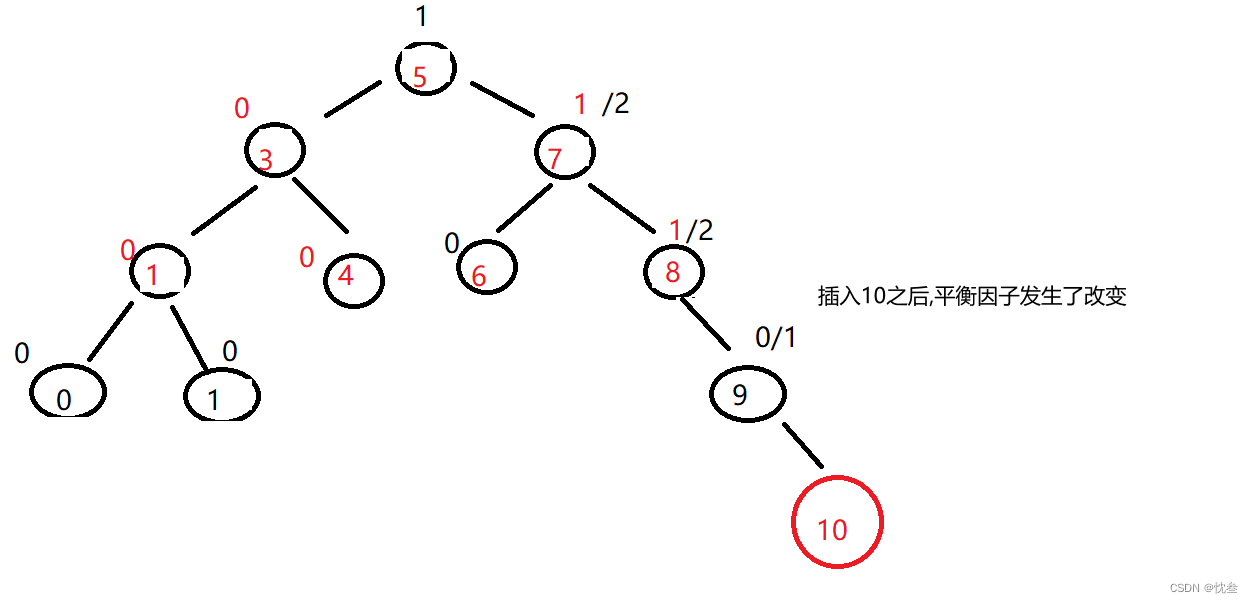
先来分析一下,假设插入的节点val是10这个时候,相当于插入到AVL树的最右边,此时 9的平衡因子++,8的平衡因子++,但是以8节点为根这个二叉树不是高度平衡的了,所以需要进行旋转!!!
先来构造一颗AVL树
public class AVLTree {
static class TreeNode {
public int val;
public int bf; // 平衡因子
public TreeNode left;
public TreeNode right;
public TreeNode parent;
public TreeNode(int val) {
this.val = val;
}
}
public TreeNode root;// 根节点
插入的具体代码实现
public boolean insert(int val){
TreeNode parent = null;
TreeNode node = new TreeNode(val);
if(root == null){
root = node;
return true;
}
//root不为空,不是第一次插入
TreeNode cur = root;
while(cur != null){
if(cur.val < val){
parent = cur;
cur = cur.right;
}else if(cur.val == val){
return false;
}else{
parent = cur;
cur = cur.left;
}
}
//走到这里之后,cur = null,此时也找到了插入的地方
if(parent.val < val){
parent.right= node;
cur = node;
}else{
parent.left = node;
cur = node;
}
//双向指向
node.parent = parent;
//完成了插入,就需要去检查相关节点的平衡因子,发现某个节点的平衡因子不对,就需要进行旋转,并且向上进行检查
while(parent != null){
if(cur == parent.left){
parent.bf--;
}else{
parent.bf++;
}
//检查当前平衡因子是否满足
if(parent.bf == 0){
//因为是从parent下面去插入的,parent.bf最可能是不满足的才会引发连锁导致上面的也不满足,如果是满足的就不需要去向上检查了
break;
}else if(parent.bf == 1 || parent.bf == -1){
//当前是满足,但是向上检查不一定满足
cur = parent;
parent = cur.parent;
}else{
//此时就是不满足,直接进行旋转,但是不知道往哪边去旋转,需要再去判断一下
if(parent.bf == 2){
//parent.bf = 2,说明是该节点右子树高,需要进行左旋,那么为啥还要再判断cur呢???
//当走到这里的时候,bf = 2,说明这个parent下面是有右节点的,这个右节点下面肯定是有节点cur,否则不可能为2
//但是cur的孩子是左还是右我们不知道,这个也需要进行讨论
if(cur.bf == 1){
//cur的孩子是右,左旋
rotateLeft(parent);
}else{
//cur.bf = -1 右旋
rotateRL(parent);
}
}else{
//parent.bf = -2;左树高就需要降低左树高度
if(cur.bf == 1){
rotateLR(parent);
}else{
rotateRight(parent);
}
}
break;
}
}
return true;
}
关于插入分好几种情况,影响平衡因子的情况也是不同的
这种是在cur的右边插入,解决办法就是左单旋,因为 parent 和 cur的平衡因子都是同号的,只需一次单旋即可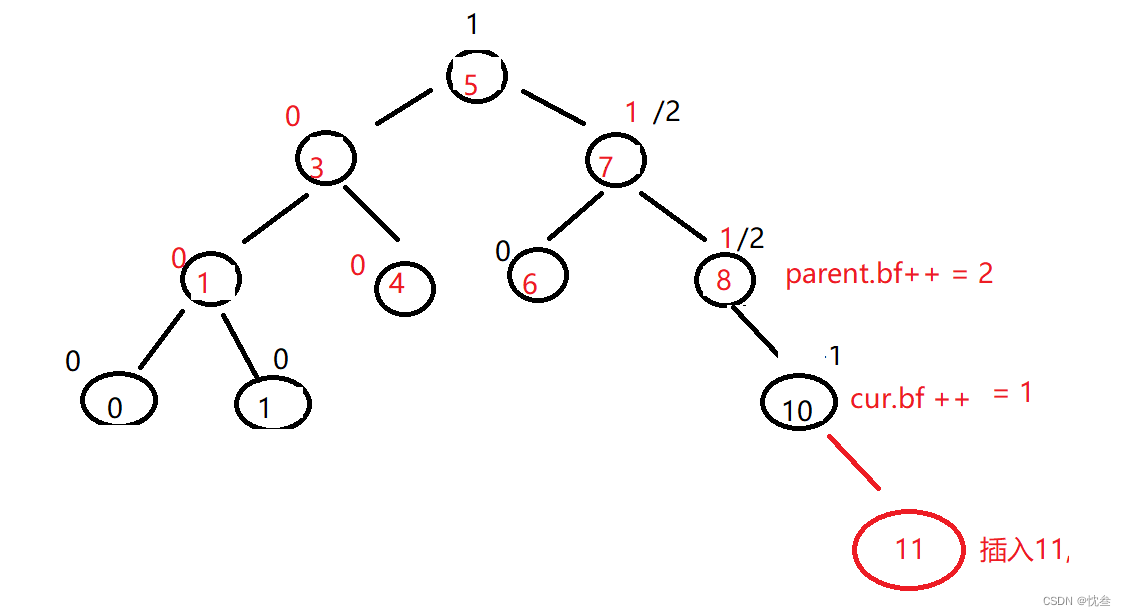
这种是在cur的左边插入,解决办法就是右左双旋旋,因为 parent 和 cur的平衡因子都是异号的,先右旋,但是这个右旋的节点不是parent,而是parent.left
再去左旋parent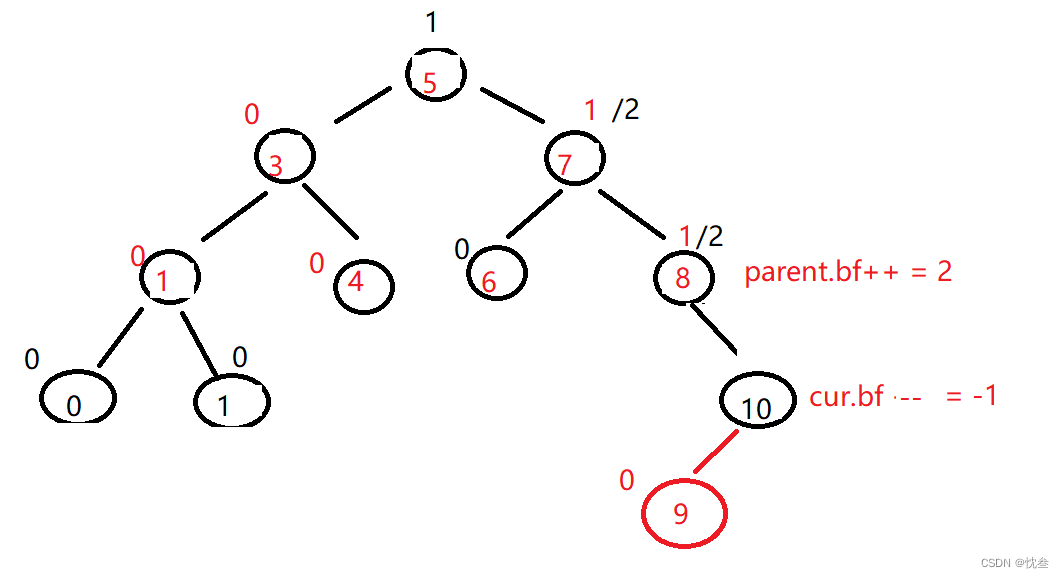
这种parent.bf = -2,但是由此又分出 cur.bf = 1或者 -1,上面介绍了同号的话就直接进行一次单旋,并且是右旋即可,这种情况是进行左右双旋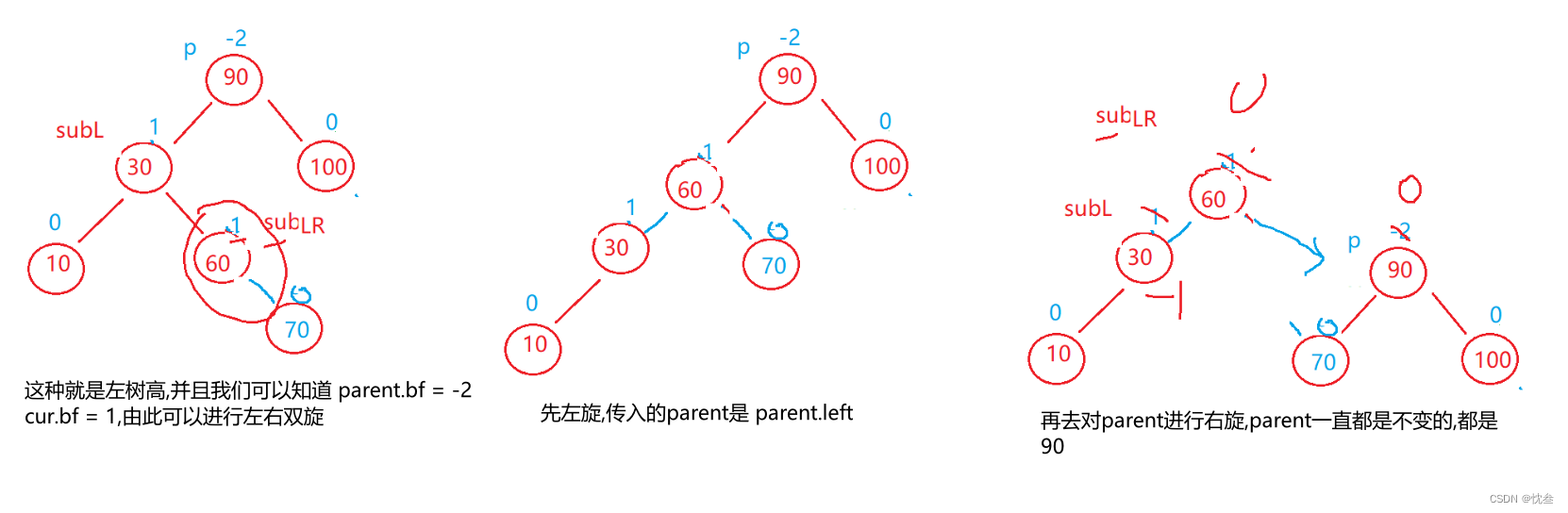
这个就是右单旋一次即可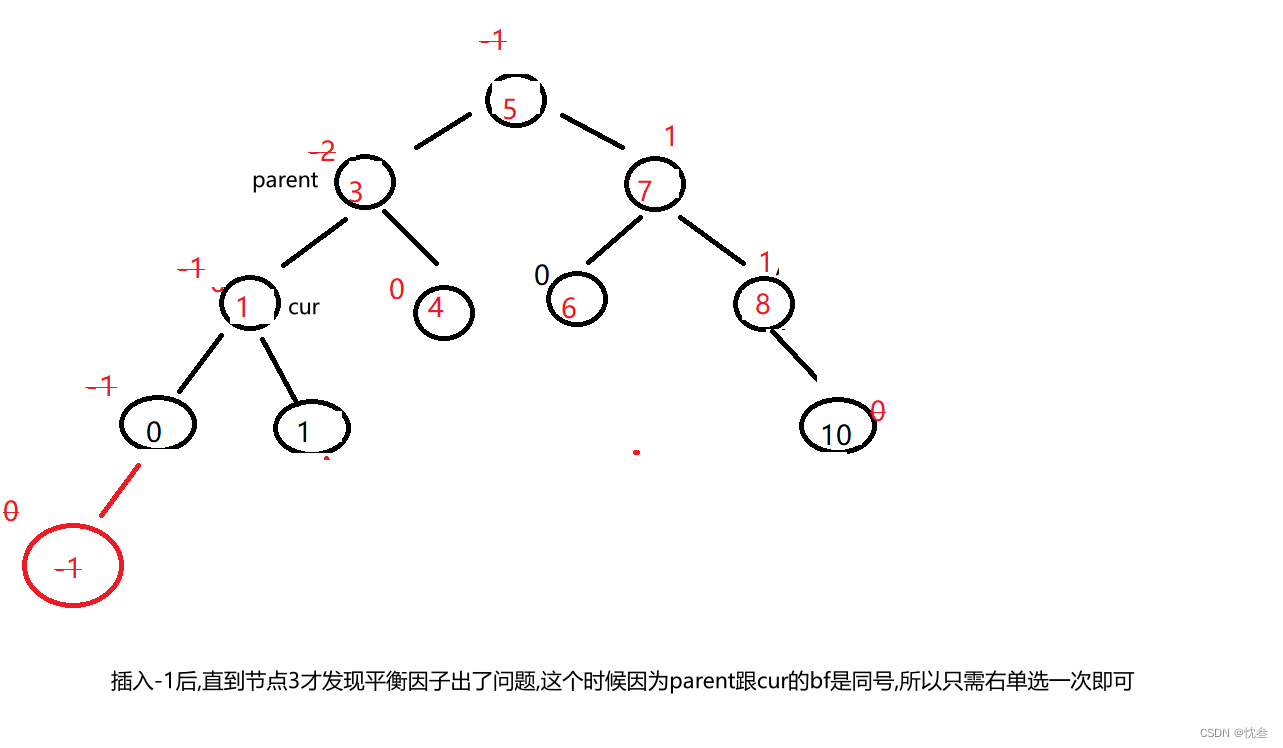
左单旋代码
public void rotateLeft(TreeNode parent) {
TreeNode subR = parent.right;
TreeNode subRL = subR.left;
parent.right = subRL;
subR.left = parent;
if (subRL != null) {
subRL.parent = parent;
}
TreeNode pParent = parent.parent;
parent.parent = subR;
if(root == parent){
root = subR;
root.parent = null;
}else{
if(pParent.left == parent){
pParent.left = subR;
}else{
pParent.right = subR;
}
subR.parent = pParent;
}
//旋转完成之后发现,这两个节点的bf 都是0
parent.bf = subR.bf = 0;
}
右单旋代码
public void rotateRight(TreeNode parent) {
//右旋 降低左树高度
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
parent.left = subLR;
subL.right = parent;
//先去判断有没有subLR
if (subLR != null) {
//在AVL树种,有parent所以存在双向引用,前面已经有了 parent.left = subRL,但是这里还需要去反向引用一下
//但是我们并不能知道subRL存不存在,所以需要判断一下
subLR.parent = parent;
}
TreeNode pParent = parent.parent;
parent.parent = subL;
if (parent == root) {
root = parent;
root.parent = null;
} else {
if (parent == pParent.left) {
subL = pParent.left;
} else {
subL = pParent.right;
}
subL.parent = pParent;
}
parent.bf = subL.bf = 0;
}
左右双旋代码
public void rotateLR(TreeNode parent){
//先左再右
TreeNode subL = parent.left;
TreeNode subLR = subL.right;
int bf = subLR.bf;
rotateLeft(parent.left);
rotateRight(parent);
if(bf == -1) {
subL.bf = 0;
subLR.bf = 0;
parent.bf = 1;
}else if(bf == 1){
subL.bf = -1;
subLR.bf = 0;
parent.bf = 0;
}
}
右左双旋
public void rotateRL(TreeNode parent){
//先右再左
TreeNode subR = parent.right;
TreeNode subRL = subR.left;
int bf = subRL.bf;
rotateRight(parent.left);
rotateLeft(parent);
if(bf == -1) {
subR.bf = 0;
subRL.bf = 0;
parent.bf = 1;
}else if(bf == 1){
subR.bf = -1;
subRL.bf = 0;
parent.bf = 0;
}
}
边栏推荐
- MATLAB小技巧(29)多项式拟合 plotfit
- Abnova 免疫组化服务解决方案
- Several index utilization of joint index ABC
- 隐马尔科夫模型(HMM)学习笔记
- MySQL SQL的完整处理流程
- Pinduoduo lost the lawsuit: "bargain for free" infringed the right to know but did not constitute fraud, and was sentenced to pay 400 yuan
- 2022/07/04学习记录
- Networkx绘图和常用库函数坐标绘图
- leetcode 509. Fibonacci Number(斐波那契数字)
- js装饰器@decorator学习笔记
猜你喜欢
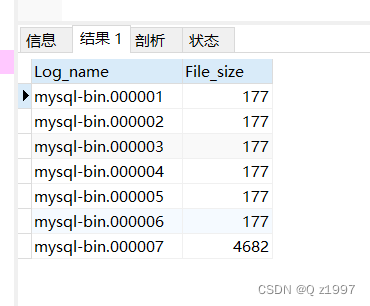
MySQL view bin log and recover data

RuntimeError: CUDA error: CUBLAS_STATUS_ALLOC_FAILED when calling `cublasCreate(handle)`问题解决
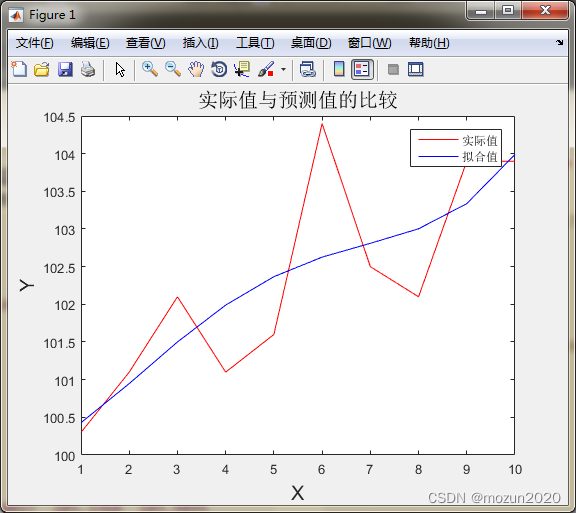
MATLAB小技巧(30)非线性拟合 lsqcurefit

Redhat5 installing vmware tools under virtual machine

Several index utilization of joint index ABC
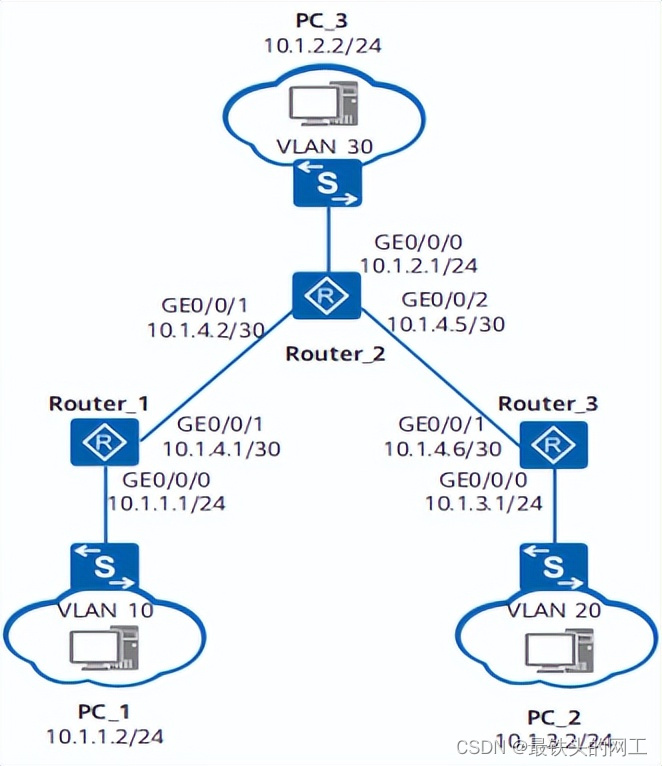
This article introduces you to the characteristics, purposes and basic function examples of static routing

jdbc数据库连接池使用问题
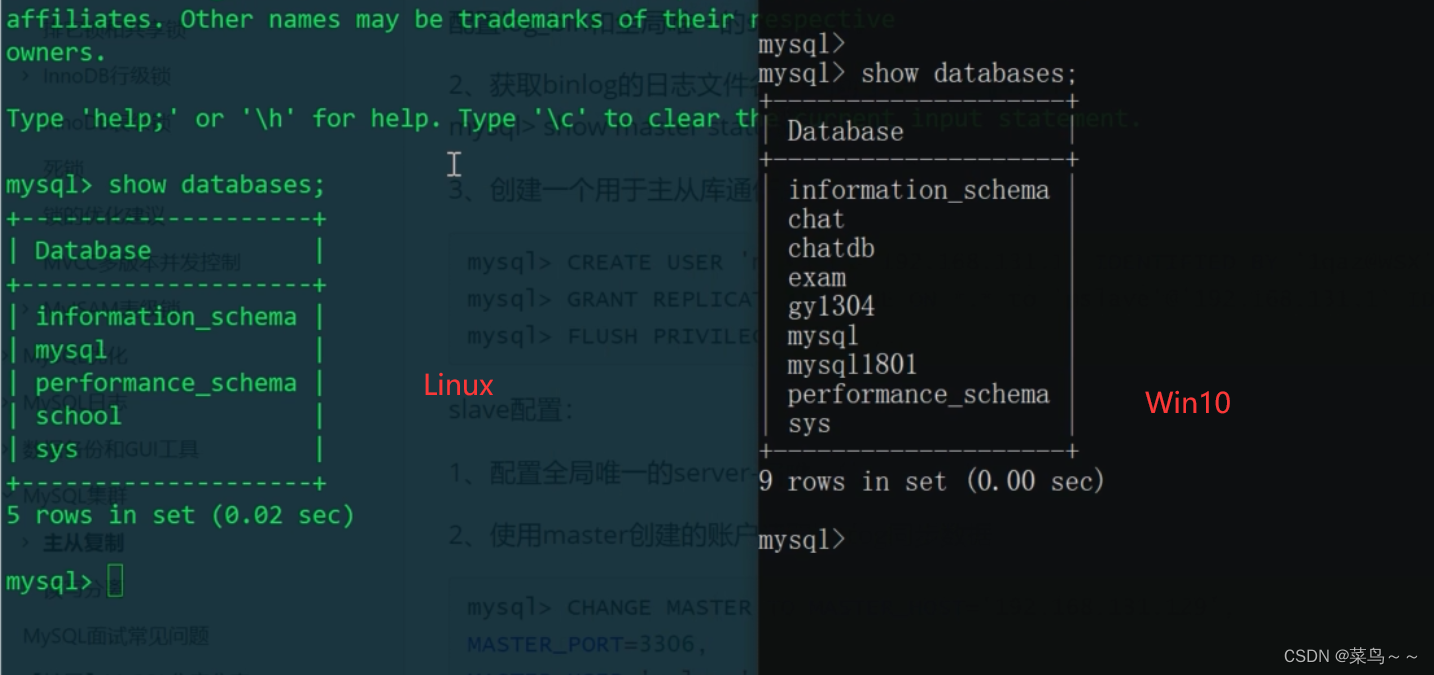
MySQL的主从复制原理

Mysql---- import and export & View & Index & execution plan

剑指offer-高质量的代码
随机推荐
BindingException 异常(报错)处理
循环肿瘤细胞——Abnova 解决方案来啦
MySQL的主从复制原理
leetcode 509. Fibonacci Number(斐波那契数字)
DHCP路由器工作原理
libcurl返回curlcode说明
华为机试题素数伴侣
Abnova循环肿瘤DNA丨全血分离,基因组DNA萃取分析
jdbc数据库连接池使用问题
Brand · consultation standardization
Leetcode T1165: 日志分析
Algorithm --- bit count (kotlin)
2018年江苏省职业院校技能大赛高职组“信息安全管理与评估”赛项任务书第二阶段答案
RuntimeError: CUDA error: CUBLAS_STATUS_ALLOC_FAILED when calling `cublasCreate(handle)`问题解决
Abnova 体外转录 mRNA工作流程和加帽方法介绍
JWT的基础介绍
Unity C# 函数笔记
7天零基础能考证HCIA吗?华为认证系统学习路线分享
JWT certification
Mysql---- import and export & View & Index & execution plan