Prime partner of Huawei machine test questions

Maximum matching of bipartite graph （ hungarian algorithm ）： Prime mate
The top
Title Description
If sum of the two positive integers is prime , Then these two positive integers are called “ Prime mate ”, Such as 2 and 5、6 and 13, They can be applied to communication encryption . Now the password society asks you to design a program , From what already exists N（N For the even ） Select several pairs of positive integers to form “ Prime mate ”, There are many options , For example, there are 4 A positive integer ：2,5,6,13, If you will 5 and 6 You can only get one group in a group “ Prime mate ”, And will be 2 and 5、6 and 13 Grouping will result in two groups “ Prime mate ”, Energy composition “ Prime mate ” The most common scheme is called “ Best solution ”, Of course, the password society wants you to find “ Best solution ”.

Input
There is a positive even number N（N≤100）, Represents the number of natural numbers to be selected . Specific figures are given later , The scope is [2,30000].

Output
Output an integer K, It means what you get “ Best solution ” form “ Prime mate ” The logarithmic .

Input description
1、 Enter a positive even number n
2 、 Input n It's an integer

Output description
Obtained “ Best solution ” form “ Prime mate ” The logarithmic .

Input
4
2 5 6 13

Output
2

Ideas
Consider using graph theory to model this problem .100 The number is 100 A little bit , If the sum of these two numbers is prime , Connect an edge between these two numbers . after , We should choose as many edges as possible , Require these edges not to share endpoints . The value range of each number is [2,30000]. Prime except 2 It's even , Others are odd numbers —— And now it can't happen 2 了 , So we only consider odd primes .2 The sum of numbers is odd , Only an odd number + even numbers . therefore , We divide these numbers into 2 Pile up —— Odd and even , Get bipartite graph . Then among them , And are prime , Connect an edge , Then match . The maximum match of bipartite graph , There is a much simpler algorithm , hungarian algorithm .

Relevant concepts
Bipartite graph
A bipartite graph is actually a graph in which all points can be divided into two groups , There are no edges in the same group , All edges span two groups . Accurately speaking ： Divide the vertex of a graph into two disjoint sets U and V , And make each side connected separately U 、V The summit of , If there is such a division , This graph is called a bipartite graph .
Another equivalent definition of bipartite graph is ： It doesn't contain 「 Rings with odd edges 」 Graph .
matching
Bipartite graph matching is the set of edges, in which any two edges have no common vertices . We define ：
Match side 、 Match points 、 Unmatched edges 、 Mismatches .
Pictured ： if 1—2 Connected to a ,5—4 Connected to a ,7—6 Connected to a . Obviously 1—2 edge 、5—4 edge 、7—6 The edge is a matching edge ,1、2、4、5、6、7 For matching points . The rest are unmatched points and unmatched edges .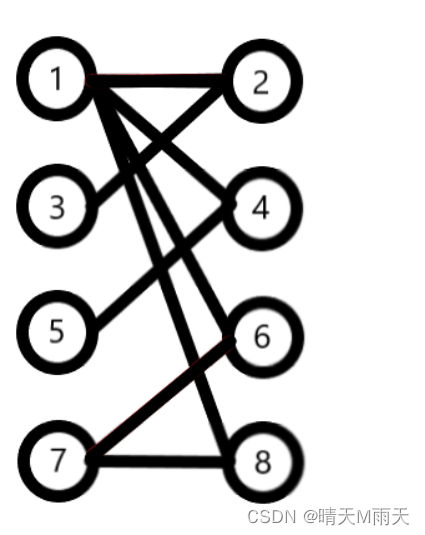

The biggest match
The matching with the largest number of edges in the matching of a graph is the maximum matching of this graph . As shown in the figure above, the maximum match is ：

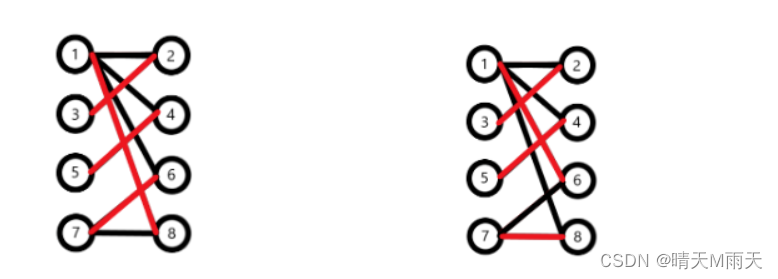
Obviously, there may be more than one maximum match .
Perfect match
If there is a match in a graph , All vertices are matching points , Then it's a perfect match . The above pictures are perfect matches . obviously , Perfect match must be the biggest match （ Any point of perfect match has been matched , Adding a new matching edge will conflict with the existing matching edge ）. But not every graph has a perfect match .
Alternate paths
Starting from an unmatched point , Pass through the unmatched edges in turn 、 Match side 、 Unmatched edges …… The formed path is called alternate path . Pictured 2—>1—>8—>7 It is an alternate path .

Augmentation path
Starting from an unmatched point , Take alternate paths , If you reach another unmatched point , Then this alternate path is called augmented path （agumenting path）. Pictured 1—>2—>3—>6—>7—>8 That is, an expansion path .
Code reference

import java.util.Scanner;
import java.util.ArrayList;

public class Main{
    
    
    static int max=0;
    public static void main(String[] args){
    
        // The standard input 
        Scanner sc=new Scanner(System.in);
        while(sc.hasNext()){
    
            // Enter positive and even numbers 
            int n=sc.nextInt();
            // Used to record input n It's an integer 
            int[] arr=new int[n];
            // Used to store all odd numbers 
            ArrayList<Integer> odds=new ArrayList<>();
            // Used to store all even numbers 
            ArrayList<Integer> evens=new ArrayList<>();
            for(int i=0;i<n;i++){
    
                arr[i]=sc.nextInt();
                // Add odd numbers to odds
                if(arr[i]%2==1){
    
                    odds.add(arr[i]);
                }
                // Add even numbers to evens
                if(arr[i]%2==0){
    
                    evens.add(arr[i]);
                }
            }
            // Subscripts correspond to even subscripts that have been matched , The value corresponds to this even number of partners 
            int[] matcheven=new int[evens.size()];
            // Record the number of partners 
            int count=0;
            for(int j=0;j<odds.size();j++){
    
                // Used to mark whether the corresponding even number has been searched 
                boolean[] v=new boolean[evens.size()];
                // If match up , Then count and add 1
                if(find(odds.get(j),matcheven,evens,v)){
    
                    count++;
                }
            }
            System.out.println(count);
        }   
    }
    
    // Judge the odd number x Can you find a partner 
    private static boolean find(int x,int[] matcheven,ArrayList<Integer> evens,boolean[] v){
    
        for(int i=0;i<evens.size();i++){
    
            // This location has not been visited even , And can communicate with x Form prime partners 
            if(isPrime(x+evens.get(i))&&v[i]==false){
    
                v[i]=true;
                /* If i Even number has no partner , Then with x Form a partner , If you already have a partner , And this partner can find a new partner ,  Then give your original partner to others , Oneself and x Form a partner */
                if(matcheven[i]==0||find(matcheven[i],matcheven,evens,v)){
    
                    matcheven[i]=x;
                    return true;
                }
            }
        }
        return false;
    }
    // Judge x Is it a prime 
    private static boolean isPrime(int x){
    
        if(x==1) return false;
        // If it can be 2 Root number x to be divisible by , Then it must not be prime 
        for(int i=2;i<=(int)Math.sqrt(x);i++){
    
            if(x%i==0){
    
                return false;
            }
        }
        return true;
    }
}