当前位置:网站首页>Binary search tree
Binary search tree
2022-07-06 18:44:00 【m0_ sixty-two million four hundred and six thousand two hundred】
1. Content arrangement description
The binary tree is in front C The data structure phase has been talked about , This section is named binary tree advanced because :
1. map and set Features need to pave the way for a binary search tree , The binary search tree is also a tree structure
2. Understand the characteristics of binary search tree , Help to understand better map and set Characteristics of
3. Some interview questions in the binary tree are a little difficult , It's not easy for everyone to accept , And it's easy to forget for a long time
4. There are some OJ Question use C Language implementation is troublesome
2. Binary search tree
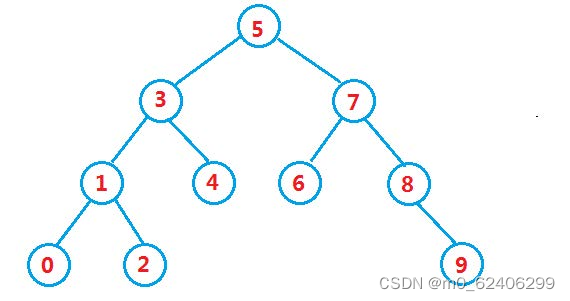
2.1 Binary search tree concept
Binary search tree is also called binary sort tree , It could be an empty tree , Or a binary tree with the following properties :
If its left subtree is not empty , Then the values of all nodes on the left subtree are smaller than the values of the root nodes
If its right subtree is not empty , Then the value of all nodes on the right subtree is greater than the value of the root node
Its left and right subtrees are also binary search trees
2.2 Binary search tree operation
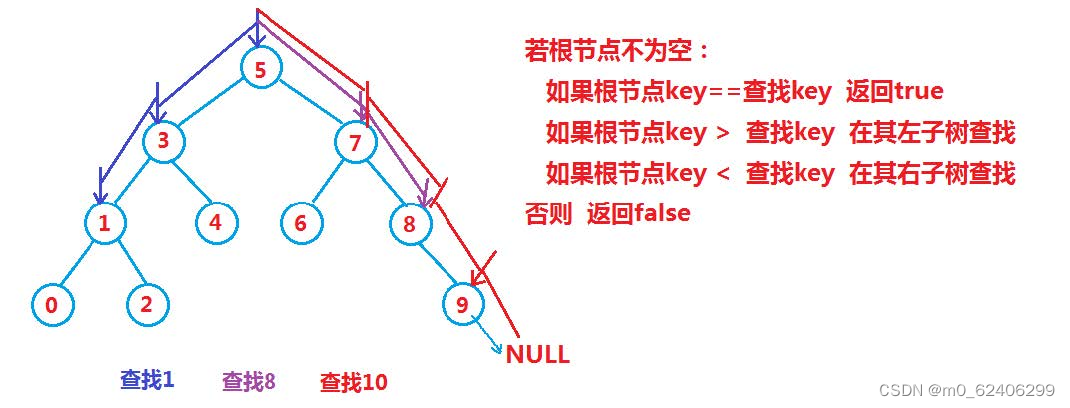
1. Binary search tree lookup
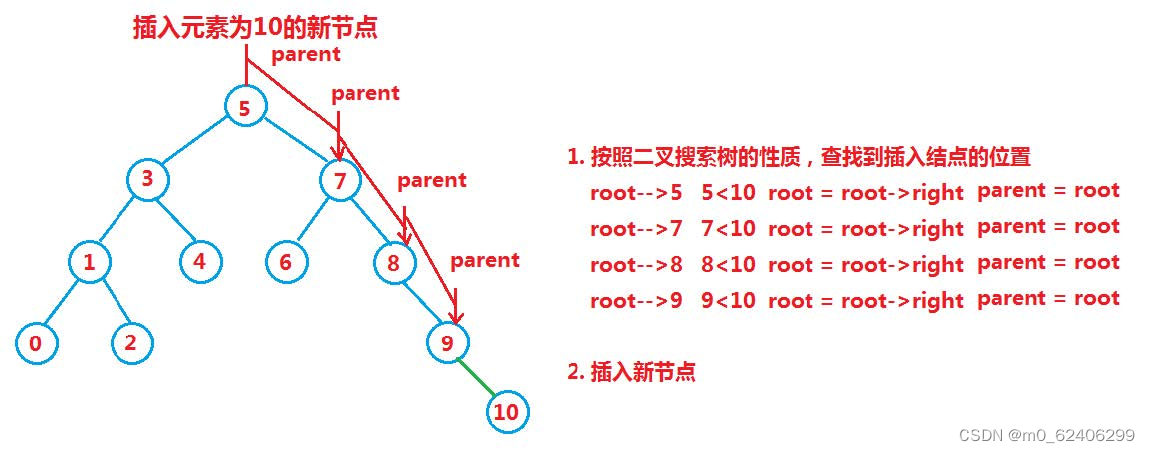
2. Binary search tree insertion
The specific process of insertion is as follows :
a. The tree is empty. , And just insert

b. The tree is not empty , Find the insertion position according to the nature of binary search tree , Insert new node
3. Deletion of binary search tree
First, find out whether the element is in the binary search tree , If it doesn't exist , Then return to , Otherwise, the nodes to be deleted may be divided into the following four situations :
a. The node to be deleted has no children
b. Only the left child node is to be deleted
c. Only the right child node is to be deleted
d. The node to be deleted has left 、 Right child node
It seems that the nodes to be deleted are 4 Medium condition , Physical truth a Can be related to the situation b perhaps c combined , So the real deletion process is as follows :
situation b: Delete the node and make the parent node of the deleted node point to the left child node of the deleted node
situation c: Delete the node and make the parent node of the deleted node point to the right child node of the deleted node
situation d: Look for the first node under the middle order in its right subtree ( Key minimum ), Fill the deleted node with its value , Then deal with the deletion of this node
2.3 Implementation of binary search tree
template<class T>
struct BSTNode
{
BSTNode(const T& data = T())
: _pLeft(nullptr) , _pRight(nullptr), _data(data)
{}
BSTNode<T>* _pLeft;
BSTNode<T>* _pRight;
T _data;
};
template<class T>
class BSTree
{
typedef BSTNode<T> Node;
typedef Node* PNode;
public:
BSTree(): _pRoot(nullptr)
{}
// Students realize it by themselves , Similar to the destruction of binary trees
~BSTree();
// Search according to the properties of binary search tree : Find the value for data The position of the node in the binary search tree
PNode Find(const T& data);
bool Insert(const T& data)
{
// If the tree is empty , Directly inserted into the
if (nullptr == _pRoot)
{
_pRoot = new Node(data);
return true;
}
// Search according to the properties of binary search tree data Insertion position in the tree
PNode pCur = _pRoot;
// Record pCur My parents , Because the new element is finally inserted in pCur The position of parents around their children
PNode pParent = nullptr;
while (pCur)
{
pParent = pCur;
if (data < pCur->_data)
pCur = pCur->_pLeft;
else if (data > pCur->_data)
pCur = pCur->_pRight; // The element already exists in the tree
else
return false;
}
// Insert elements
pCur = new Node(data);
if (data < pParent->_data)
pParent->_pLeft = pCur;
else
pParent->_pRight = pCur;
return true;
}
bool Erase(const T& data)
{
// If the tree is empty , Delete failed
if (nullptr == _pRoot)
return false;
// Find in data Position in the tree
PNode pCur = _pRoot;
PNode pParent = nullptr;
while (pCur)
{
if (data == pCur->_data)
break;
else if (data < pCur->_data)
{
pParent = pCur;
pCur = pCur->_pLeft;
}
else
{
pParent = pCur;
pCur = pCur->_pRight;
}
}
// data Not in the binary search tree , Cannot delete
if (nullptr == pCur)
return false;
// Delete in the following cases , Students draw and analyze by themselves
if (nullptr == pCur->_pRight)
{
// The current node has only the left child or the left child is empty --- It can be deleted directly
}
else if (nullptr == pCur->_pRight)
{
// The current node has only right children --- It can be deleted directly
}
else
{
// There are children on both sides of the current node , It's not easy to delete directly , You can find an alternative node in its subtree , such as :
// Find the largest node in its left subtree , That is, the rightmost node in the left subtree , Or the smallest node in its right subtree , namely
The smallest node in the right subtree
// After the replacement node is found , Give the value in the substitute node to the node to be deleted , Convert to delete substitute node
}
return true;
}
// Realize it by yourself
void InOrder();
private:
PNode _pRoot;边栏推荐
- Reproduce ThinkPHP 2 X Arbitrary Code Execution Vulnerability
- 测试行业的小伙伴,有问题可以找我哈。菜鸟一枚~
- Shangsilicon Valley JUC high concurrency programming learning notes (3) multi thread lock
- Huawei 0 foundation - image sorting
- [Sun Yat sen University] information sharing of postgraduate entrance examination and re examination
- Human bone point detection: top-down (part of the theory)
- Markdown syntax for document editing (typera)
- 星诺奇科技IPO被终止:曾拟募资3.5亿元 年营收3.67亿
- How does crmeb mall system help marketing?
- The role of applet in industrial Internet
猜你喜欢
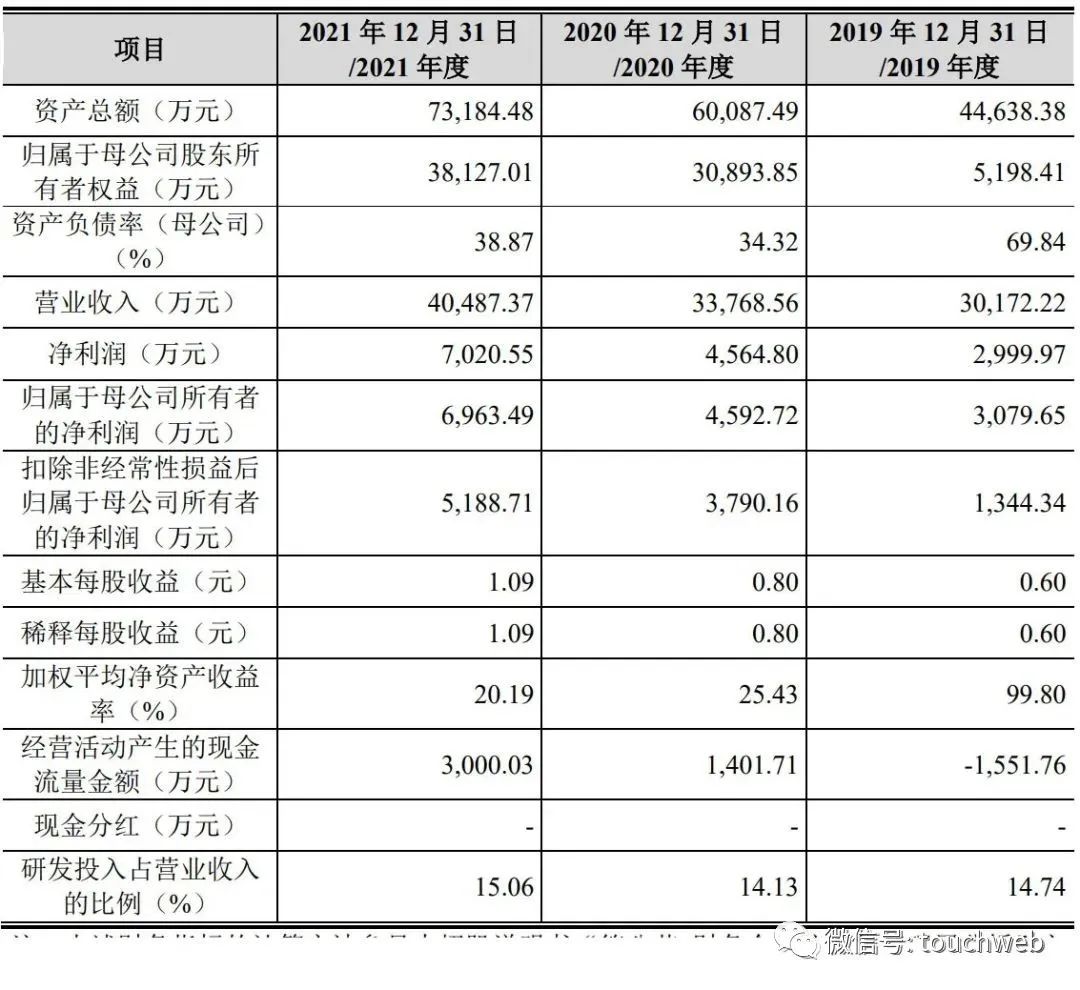
朗坤智慧冲刺科创板:年营收4亿 拟募资7亿
Docker安装Redis
win10系统下插入U盘有声音提示却不显示盘符
SQL injection - access injection, access offset injection
TOP命令详解

Describe the process of key exchange
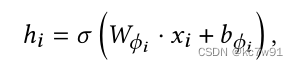
Self-supervised Heterogeneous Graph Neural Network with Co-contrastive Learning 论文阅读

人体骨骼点检测:自顶向下(部分理论)
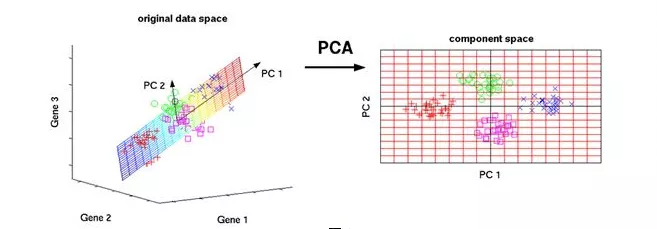
30 minutes to understand PCA principal component analysis

Introduction to the use of SAP Fiori application index tool and SAP Fiori tools
随机推荐
小程序在产业互联网中的作用
Coco2017 dataset usage (brief introduction)
AcWing 3537.树查找 完全二叉树
Describe the process of key exchange
Jushan database was among the first batch of financial information innovation solutions!
TOP命令详解
[Sun Yat sen University] information sharing of postgraduate entrance examination and re examination
C language college laboratory reservation registration system
Epoll () whether it involves wait queue analysis
Stm32+mfrc522 completes IC card number reading, password modification, data reading and writing
POJ 2208 已知边四面体六个长度,计算体积
STM32+HC05串口蓝牙设计简易的蓝牙音箱
atcoder它A Mountaineer
win10系统下插入U盘有声音提示却不显示盘符
具体说明 Flume介绍、安装和配置
[Matlab] Simulink 同一模块的输入输出的变量不能同名
Shangsilicon Valley JUC high concurrency programming learning notes (3) multi thread lock
Breadth first traversal of graph
Docker安装Redis
STM32+MFRC522完成IC卡号读取、密码修改、数据读写