Li Kou today's question -729 My schedule I

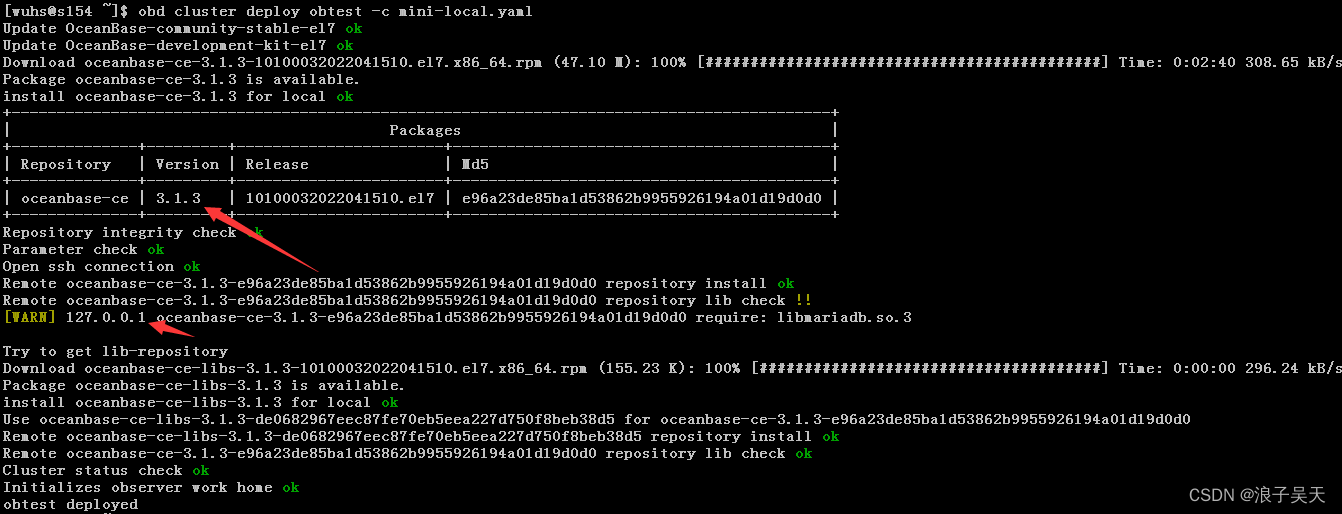
729. My schedule I

Two points

1. First, sort all the scheduled sequences , Then traverse the interval in turn , Look at a certain interval left1, Is it greater than end

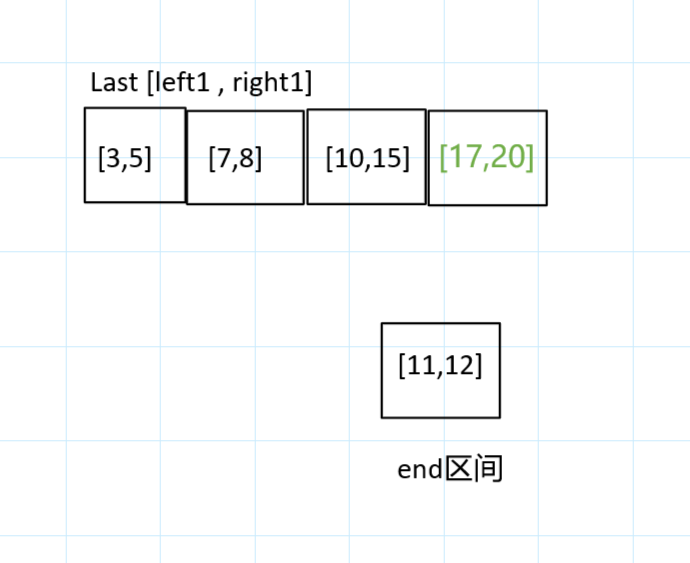
12 Hui He 3,5,10 Compare , It will be found that there is no larger range , It's time to consider inserting them behind .

• Not found ： That's the same as the last interval right1 Compare , Look at the last interval right1 Whether it is smaller than the insertion interval start, If you can, return to ture, Otherwise it returns false

12 And the last element 15 Compare , Find out 15 It is greater than 12 Of , return false.

and 17 The first and 3,7,10 Compare , Found that they are bigger than them , So consider putting it back , then 20 and 15 Compare , Find out 20 Greater than 15, return true.

• Judge to find the first

I. judgment , Found end Be smaller than the smallest left1, So you can insert , Just go back to true

• Intermediate insertion

Intermediate interval , find last The last interval of pre[left2,right2], if right2 Be greater than start, Then there is intersection , return false, Otherwise return to true.

First judge , Find out 10==10, Stop and judge 7, Take a look 7<8 There is intersection , return false.

such as [9,10] This is a correct example , Find out 10 =- 10, Stop and judge , Take a look 9> 8, return true.

• Code ：

    List<int[]> data;

    public MyCalendar() {
        data = new ArrayList<>();
    }

    public boolean book(int start, int end) {
        if (data.size() == 0) {
            data.add(new int[]{start, end});
            return true;
        }
        data.sort(Comparator.comparingInt(o -> o[0]));
        int left = 0, right = data.size() - 1;
        // Find the first start >= end The range of 
        int ans = -1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (data.get(mid)[0] >= end) {
                ans = mid;
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        // Can't find   Compare with the last interval 
        if (ans == -1) {
            int[] ints = data.get(data.size() - 1);
            if (ints[1] > start) {
                return false;
            }
        } else if (ans != 0) {
            // Not the first interval , If it is the first interval, you can directly insert 
            int[] pre = data.get(ans - 1);
            if (pre[1] > start) {
                return false;
            }
        }
        data.add(new int[]{start, end});
        return true;
    }

Direct traversal

class MyCalendar {
    //  Define a booked
    List<int[]> booked;
    public MyCalendar() {
        booked = new ArrayList<int[]>();
    }
    
    public boolean book(int start, int end) {
        for(int[] arr : booked){
            int l = arr[0] ,r = arr[1];
            // The second case 
            if(l < end && start < r){
                return false;
            }
        }
        booked.add(new int[]{start,end});
        return true;
    }
}

/**
 * Your MyCalendar object will be instantiated and called as such:
 * MyCalendar obj = new MyCalendar();
 * boolean param_1 = obj.book(start,end);
 */

[s1,e1) and [s2,e2), No intersection is satisfied s1>e2 perhaps s2>e1, On the contrary, it means that the two return to produce intersection .

Train of thought three

Change your mind , The concept of overlap can be extended to the generalized concept of equality , That is, once overlapped, it means that the two elements are equal , Then it's simple ,set Specially used for de duplication storage . that HashSet and TreeSet Which one to use ？ First HashSet De duplication is based on the hash value of the object , Because what we want to store is int[] Type of , When we write code, we should base on start and end To create it , Then their hash values are basically different , That is to say, even two int[] The values inside are exactly the same , But the hash value is different ,HashSet They will also be stored . Because we regard overlap as equality in a broad sense , Then we need to define a comparator to distinguish whether their generalized equality , and TreeSet Support custom comparator , And sort according to the value returned by the comparator , Very much in line with our needs .

class MyCalendar {
    // Define a TreeSet
    TreeSet<int[]> calendars;

    public MyCalendar() {
        calendars = new TreeSet<>((a, b) -> {
            if(a[1] <= b[0])
                return -1;
            else if(a[0] >= b[1])
                return 1;
            else
                return 0;
        });
    }
    
    public boolean book(int start, int end) {
        int[] e = new int[]{start, end};
        return calendars.add(e);
    }
}
/**
 * Your MyCalendar object will be instantiated and called as such:
 * MyCalendar obj = new MyCalendar();
 * boolean param_1 = obj.book(start,end);
 */

expand

TreeSet brief introduction ： Orderly , Do not repeat , Red and black trees , be based on Treemap Realization , Custom sorting and other features .

TreeSet It's an ordered set , Its function is to provide order Set aggregate . It is inherited from AbstractSet abstract class , Realized NavigableSet , Cloneable, java.io.Serializable Interface .
TreeSet Inherited from AbstractSet, So it's a Set aggregate , have Set Properties and methods of .
TreeSet Realized NavigableSet Interface , It means that it supports a range of navigation methods . For example, find the best match with the specified target .
TreeSet Realized Cloneable Interface , It means it can be cloned .
TreeSet Realized java.io.Serializable Interface , Means it supports serialization .
TreeSet Is based on TreeMap Realized .TreeSet The elements in support 2 Sort by ： Natural ordering perhaps According to create TreeSet Provided by Comparator Sort . It depends on the construction method used .
TreeSet For basic operation （add、remove and contains） Provide guaranteed log(n) Time cost .
in addition ,TreeSet asynchronous . its iterator The iterator returned by the method is fail-fast Of