当前位置:网站首页>Kinematics Analysis of Robot Arm
Kinematics Analysis of Robot Arm
2022-08-02 05:03:00 【Elegance and classmates】
When doing competitions before, it was necessary to grab the specified object through the robotic arm,Because the action group that executes the specified robotic arm is not flexible enough,And it can not meet the actual needs very well,Therefore, the kinematics analysis of the manipulator is adopted,Realize the grasping of the robotic arm.
源代码如下:
import math
""" pythonRobotic arm analysis of procedural kinematics 输入的参数:The length of the three links、X,Y,Z的坐标点 输出的参数:The angle of rotation of the four servos(j0,j1,j2,j3) 注:j4、j5The angle is determined by vision """
RAD2ANG = 3.1415926535898 / 180.0
# The length of the three links
L1 = 10.5
L2 = 9.5
L3 = 17
""" Robotic arm documentation 注:The following is an explanation from the angle of the robotic arm:1代表着45° 0号舵机-->-90°~90°(向左为正) 0°is the center 1号舵机-->-90°~90°(向下为正) 0°is directly above 2号舵机-->-90°~90°(向后为正) 0°is directly above 3号舵机-->-90°~90°(向后为正) 0°is directly above 4号舵机-->-90°~90°(逆时针为正) 0°cross claw 5号舵机-->0°~45°(向右为正) 0°to close the paws """
def and2Rad(N):
return (N) * (180.0 / 3.1415926535898)
def angleToJoint(angle):
return angle * (1 / 45)
def jointToAngle(joint):
return joint * 45
def nowAngle():
# What is obtained is the angle corresponding to the current rotation of each servojoint值
print("now joint:")
i = 0
for joint in arm.GetJointState():
print("joint" + str(i) + ":" + str(jointToAngle(joint)))
i += 1
def inverseKinematics(x, y, z, L1, L2, L3):
""" 运动学逆解:通过传入的X,Y,ZAnd the length of the three-axis robotic arm to get the angle of rotation of each servo(Note that only the first four angles are found,The latter two angles need to be adjusted according to the attitude of the target) 注意:这里的0,1,2,3表示的为j1,j2,j3,j4 """
global final_j2, final_j3, final_j1, final_j0
i = 0
nearest_j3 = 1000
j0 = math.atan2(y, x)
a = x / math.cos(j0)
if (x == 0):
a = y
b = z
for j1 in range(-90, 90):
j1 *= RAD2ANG
try:
j3 = math.acos((pow(a, 2) + pow(b, 2) + pow(L1, 2) - pow(L2, 2) - pow(L3, 2) - 2 * a * L1 * math.sin(
j1) - 2 * b * L1 * math.cos(j1)) / (2 * L2 * L3))
m = L2 * math.sin(j1) + L3 * math.sin(j1) * math.cos(j3) + L3 * math.cos(j1) * math.sin(j3)
n = L2 * math.cos(j1) + L3 * math.cos(j1) * math.cos(j3) - L3 * math.sin(j1) * math.sin(j3)
t = a - L1 * math.sin(j1)
p = math.pow(math.pow(n, 2) + math.pow(m, 2), 0.5)
q = math.asin(m / p)
j2 = math.asin(t / p) - q
x1 = (L1 * math.sin(j1) + L2 * math.sin(j1 + j2) + L3 * math.sin(j1 + j2 + j3)) * math.cos(j0)
y1 = (L1 * math.sin(j1) + L2 * math.sin(j1 + j2) + L3 * math.sin(j1 + j2 + j3)) * math.sin(j0)
z1 = L1 * math.cos(j1) + L2 * math.cos(j1 + j2) + L3 * math.cos(j1 + j2 + j3)
j1 = and2Rad(j1)
j2 = and2Rad(j2)
j3 = and2Rad(j3)
# There is an error between the inverse solution and the positive solution(-0.1,0.1)It is considered that the analysis of kinematics has been completed
if (x + 0.1) > x1 > (x - 0.1) and (y + 0.1) > y1 > (y - 0.1) and (z + 0.1) > z1 > (z - 0.1):
if -90 < j1 < 90 and 0 < j2 < 180 and -90 < j3 < 180:
# 选取的是j3最接近90°The coordinates of the robotic arm change,That is, the angle at which the robotic arm is closest to the vertical downward direction
if abs(j3 - 90) < nearest_j3:
nearest_j3 = abs(j3 - 90)
# print("j0:%f,j1:%f,j2:%f,j3:%f,x:%f,y:%f,z:%f\r\n" %(and2Rad(j0), j1, j2, j3, x1, y1, z1))
final_j0 = and2Rad(j0)
final_j1 = j1
final_j2 = j2
final_j3 = j3
i = 1
except:
# print("值出现Nan")
pass
for j1 in range(-90, 90):
j1 *= RAD2ANG
try:
j3 = math.acos((math.pow(a, 2) + math.pow(b, 2) + math.pow(L1, 2) - math.pow(L2, 2) - math.pow(L3,
2) - 2 * a * L1 * math.sin(
j1) - 2 * b * L1 * math.cos(j1)) / (2 * L2 * L3))
m = L2 * math.sin(j1) + L3 * math.sin(j1) * math.cos(j3) + L3 * math.cos(j1) * math.sin(j3)
n = L2 * math.cos(j1) + L3 * math.cos(j1) * math.cos(j3) - L3 * math.sin(j1) * math.sin(j3)
t = a - L1 * math.sin(j1)
p = math.pow(math.pow(n, 2) + math.pow(m, 2), 0.5)
q = math.asin(m / p)
j2 = -(math.asin(t / p) - q)
x1 = (L1 * math.sin(j1) + L2 * math.sin(j1 + j2) + L3 * math.sin(j1 + j2 + j3)) * math.cos(j0)
y1 = (L1 * math.sin(j1) + L2 * math.sin(j1 + j2) + L3 * math.sin(j1 + j2 + j3)) * math.sin(j0)
z1 = L1 * math.cos(j1) + L2 * math.cos(j1 + j2) + L3 * math.cos(j1 + j2 + j3)
j1 = and2Rad(j1)
j2 = and2Rad(j2)
j3 = and2Rad(j3)
if (x + 0.1) > x1 > (x - 0.1) and (y + 0.1) > y1 > (y - 0.1) and (z + 0.1) > z1 > (z - 0.1):
if -90 < j1 < 90 and 0 < j2 < 180 and -90 < j3 < 180:
if abs(j3 - 90) < nearest_j3:
nearest_j3 = abs(j3 - 90)
# print("j0:%f,j1:%f,j2:%f,j3:%f,x:%f,y:%f,z:%f\r\n" %(and2Rad(j0), j1, j2, j3, x1, y1, z1))
final_j0 = and2Rad(j0)
final_j1 = j1
final_j2 = j2
final_j3 = j3
i = 1
except:
# print("值出现Nan")
pass
if i == 0:
print("无解")
return None
else:
return final_j0, final_j1, final_j2, final_j3
if __name__ == '__main__':
# given coordinates
x = 15
y = 0
z = -13.5
# Convert coordinates to angles
if inverseKinematics(x, y, z, L1, L2, L3) is None:
print("无解")
else:
j0, j1, j2, j3 = inverseKinematics(x, y, z, L1, L2, L3)
print("j0=%f,j1=%f,j2=%f,j3=%f\n" % (j0, j1, j2, j3))
边栏推荐
- 【Popular Science Post】UART Interface Communication Protocol
- 【nRF24L01 connects with Arduino to realize wireless communication】
- 引擎开发日志:重构骨骼动画系统
- 回溯法 & 分支限界 - 2
- 【MQ-3 Alcohol Detector and Arduino Detect Alcohol】
- IoT solution
- CCF刷题之旅--第一题
- 使用飞凌嵌入式IMX6UL-C1板子——qt+opencv环境搭建
- 【网络基础】浏览器输入一个URL之后,都发生了什么(详细讲解)
- PCIE电路设计
猜你喜欢

VCA821可变增益放大器

判断子序列 —— LeetCode-392

Case | industrial iot solutions, steel mills high-performance security for wisdom

bluez5.50蓝牙文件传输

【plang 1.4.6】Plang高级编程语言(发布)

联阳(ITE)IT66021FN:HDMI转RGB芯片 3D 资料

基础IO(上):文件管理和描述符

全加器高进位和低进位的理解
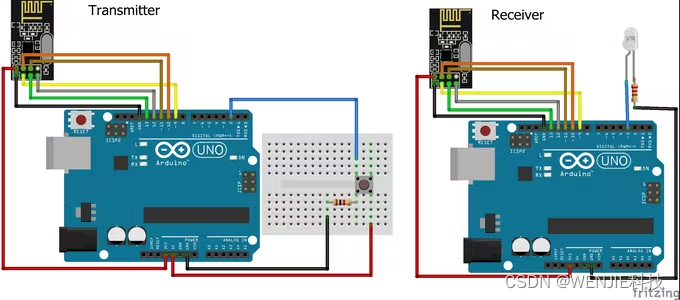
【nRF24L01 connects with Arduino to realize wireless communication】

GM8775C MIPI转LVDS调试资料分享
随机推荐
C语言教程 - 制作单位转换器
78XX 79XX多路输出电源
【Popular Science Post】Detailed explanation of MDIO interface
USB2.0一致性测试方法_高速示波器
idea中创建jsp项目详细步骤
AD实战篇
全加器高进位和低进位的理解
Personal image bed construction based on Alibaba Cloud OSS+PicGo
引擎开发日志:重构骨骼动画系统
LT8918L LVDS转MIPI芯片技术支持资料
龙芯2K1000使用nfs挂载文件系统进行使用
【操作系统】线程安全保护机制
【TCS3200 color sensor and Arduino realize color recognition】
进程(下):进程控制、终止、等待、替换
与TI的lvds芯片兼容-GM8284DD,GM8285C,GM8913,GM8914,GM8905C,GM8906C,国腾振芯LVDS类芯片,
振芯科技GM8285C:功能TTL转LVDS芯片简介
Altium Designer基础知识
电子密码锁_毕设‘指导’
联阳(ITE)IT66021FN:HDMI转RGB芯片 3D 资料
Cadence allegro导出Gerber文件(制板文件)图文操作