当前位置:网站首页>Naive Bayesian Method of Li Hang's "Statistical Learning Methods" Notes
Naive Bayesian Method of Li Hang's "Statistical Learning Methods" Notes
2022-08-02 09:33:00 【timerring】
第4章朴素贝叶斯法
Naive is a strong assumption of the whole algorithm,That is, the variables are strongly independent of each other.
例子
L take out3beans,两颗红豆1mung bean,Passers-by and I each smoked one,Passers-by found himself is in the green beans,He wants to trade the rest with me,I can't change?change beans,Is the probability of drawing red beans the same??
P ( A ∣ B ) P(A \mid B) P(A∣B) 表示在B发生的条件下发生A的概率.
P ( A ∣ B ) = P ( A B ) P ( B ) = P ( B ∣ A ) P ( A ) P ( B ) P(A \mid B)=\frac{P(A B)}{P(B)}=\frac{P(B \mid A) P(A)}{P(B)} P(A∣B)=P(B)P(AB)=P(B)P(B∣A)P(A)
设AIndicates that I drew red beans,BIndicates that the passers-by drew green beans
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) = 1 ⋅ 1 3 1 = 1 3 P(A \mid B)=\frac{P(B \mid A) P(A)}{P(B)}=\frac{1 \cdot \frac{1}{3}}{1}=\frac{1}{3} P(A∣B)=P(B)P(B∣A)P(A)=11⋅31=31
Note a misunderstanding here,Since it is knownBUnder the premise of drawing green beans,因此,这里 P ( B ) = 1 P(B)=1 P(B)=1而不是 2 3 \frac{2}{3} 32.
结论:If you want red beans,Better to exchange with passers-by.If you want green beans,最好不要换.
Suppose there is a handwritten dataset,里面有100条记录,其中第0-9条记录是10individually written0.10-19条是10individually written1.…….第90-99条是10individually written10,write a numberX,How can you tell what the number is??
How Naive Bayes Works:
P ( Y = 0 ∣ X ) = ? , P ( Y = 1 ∣ X ) = ? , ⋯ ⋯ , P ( Y = 10 ∣ X ) = ? P(Y=0 \mid X)=?, P(Y=1 \mid X)=?, \cdots \cdots, P(Y=10 \mid X)=? P(Y=0∣X)=?,P(Y=1∣X)=?,⋯⋯,P(Y=10∣X)=?
Find the one with the highest probability,就是对应的数字.
数学表达就是:
For the handwritten dataset just now, We set digital category $C_{k}, C_{0} $表示数字 $0, \cdots \cdots $.Digital discriminant formula can be modified for just now P ( Y = C k ∣ X = x ) . P\left(Y=C_{\mathbf{k}} \mid X=x\right)_{\text {. }} P(Y=Ck∣X=x).
P ( Y = C k ∣ X = x ) = P ( X = x ∣ Y = C k ) P ( Y = C k ) P ( X = x ) = P ( X = x ∣ Y = C k ) P ( Y = C k ) ∑ k P ( X = x , Y = C k ) = P ( X = x ∣ Y = C k ) P ( Y = C k ) ∑ k P ( X = x ∣ Y = C k ) P ( Y = C k ) \begin{aligned} P\left(Y=C_{\mathrm{k}} \mid X=x\right)=& \frac{P\left(X=x \mid Y=C_{k}\right) P\left(Y=C_{k}\right)}{P(X=x)} \\ =& \frac{P\left(X=x \mid Y=C_{k}\right) P\left(Y=C_{k}\right)}{\sum_{k} P\left(X=x, Y=C_{k}\right)} \\ =& \frac{P\left(X=x \mid Y=C_{k}\right) P\left(Y=C_{k}\right)}{\sum_{k} P\left(X=x \mid Y=C_{k}\right) P\left(Y=C_{k}\right)} \end{aligned} P(Y=Ck∣X=x)===P(X=x)P(X=x∣Y=Ck)P(Y=Ck)∑kP(X=x,Y=Ck)P(X=x∣Y=Ck)P(Y=Ck)∑kP(X=x∣Y=Ck)P(Y=Ck)P(X=x∣Y=Ck)P(Y=Ck)
and since each image is8x8的像素点组成,can be viewed as a one-dimensional64数组,Here is the sampleX拆开
P ( X = x ∣ Y = C k ) = P ( X ( 1 ) = x ( 1 ) ∣ Y = C k ) P ( X ( 2 ) = x ( 2 ) ∣ Y = C k ) ⋯ P ( X ( j ) = x ( j ) ∣ Y = C k ) = ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) \begin{aligned} \mathrm{P}\left(X=x \mid Y=C_{k}\right) &=P\left(X^{(1)}=x^{(1)} \mid Y=C_{k}\right) P\left(X^{(2)}=x^{(2)} \mid Y=C_{k}\right) \cdots P\left(X^{(j)}=x^{(j)} \mid Y=C_{k}\right) \\ &=\prod_{j} P\left(X^{(j)}=x^{(j)} \mid Y=C_{k}\right) \end{aligned} P(X=x∣Y=Ck)=P(X(1)=x(1)∣Y=Ck)P(X(2)=x(2)∣Y=Ck)⋯P(X(j)=x(j)∣Y=Ck)=j∏P(X(j)=x(j)∣Y=Ck)
因此上式可以化简为:
KaTeX parse error: Expected 'EOF', got '&' at position 45: …d X = x\right) &̲ = \frac{P\left…
f ( x ) = argmax C k P ( Y = C k ∣ X = x ) = P ( Y = C k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) ∑ k P ( Y = C k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) = P ( Y = C k ) ∏ j P ( X ( j ) = x ( j ) ∣ Y = C k ) \begin{aligned} f(x)=\underset{C_{k}}{\operatorname{argmax}} P\left(Y=C_{k} \mid X=x\right) &=\frac{P\left(Y=C_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} \mid Y=C_{k}\right)}{\sum_{k} P\left(Y=C_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} \mid Y=C_{k}\right)} \\ &=P\left(Y=C_{k}\right) \prod_{j} P\left(X^{(j)}=x^{(j)} \mid Y=C_{k}\right) \end{aligned} f(x)=CkargmaxP(Y=Ck∣X=x)=∑kP(Y=Ck)∏jP(X(j)=x(j)∣Y=Ck)P(Y=Ck)∏jP(X(j)=x(j)∣Y=Ck)=P(Y=Ck)j∏P(X(j)=x(j)∣Y=Ck)
其中 argmax C k \underset{C_{k}}{\operatorname{argmax}} CkargmaxIt means to find the one that maximizes the probability of the latter C k C_{k} Ck,其中:
∑ k ∏ j p ( X ( j ) = x ( j ) ∣ Y = C k ) p ( Y = C k ) = ∑ k ∑ j p ( X ( j ) = x ( j ) , Y = C k ) = ∑ j P ( X ( j ) = x ( j ) ) = P ( X = x ) \begin{array}{l} \sum_{k} \prod_{j} p\left(X^{(j)}=x^{(j)} \mid Y=C_k) p(Y=C_k)\right. \\ =\sum_{k } \sum_{j} p\left(X^{(j)}=x^{(j)}, Y=C_{k}\right)=\sum_{j} P\left(X^{(j)}=x^{(j)}\right) \\ =P(X=x) \end{array} ∑k∏jp(X(j)=x(j)∣Y=Ck)p(Y=Ck)=∑k∑jp(X(j)=x(j),Y=Ck)=∑jP(X(j)=x(j))=P(X=x)
朴素贝叶斯法的参数估计
极大似然估计
在朴素贝叶斯法中, 学习意味着估计 P ( Y = c k ) P\left(Y=c_{k}\right) P(Y=ck) 和 P ( X ( j ) = x ( j ) ∣ Y = c k ) P\left(X^{(j)}=x^{(j)} \mid Y=c_{k}\right) P(X(j)=x(j)∣Y=ck) .可以 Apply maximum likelihood estimation to estimate corresponding probabilities.先验概率 P ( Y = c k ) P\left(Y=c_{k}\right) P(Y=ck) 的极大似然估计是
P ( Y = c k ) = ∑ i = 1 N I ( y i = c k ) N , k = 1 , 2 , ⋯ , K P\left(Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)}{N}, \quad k=1,2, \cdots, K P(Y=ck)=N∑i=1NI(yi=ck),k=1,2,⋯,K
设第 j 个特征 $x^{(j)} $ 可能取值的集合为 { a j 1 , a j 2 , ⋯ , a j S j } \left\{a_{j 1}, a_{j 2}, \cdots, a_{j S_{j}}\right\} { aj1,aj2,⋯,ajSj}, 条件概率 P ( X ( j ) = a j l ∣ Y = c k ) P\left(X^{(j)}=a_{j l} \mid Y=\right. \left.c_{k}\right) P(X(j)=ajl∣Y=ck) 的极大似然估计是
P ( X ( j ) = a j l ∣ Y = c k ) = ∑ i = 1 N I ( x i ( j ) = a j l , y i = c k ) ∑ i = 1 N I ( y i = c k ) j = 1 , 2 , ⋯ , n ; l = 1 , 2 , ⋯ , S j ; k = 1 , 2 , ⋯ , K \begin{array}{l} P\left(X^{(j)}=a_{j l} \mid Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(x_{i}^{(j)}=a_{j l}, y_{i}=c_{k}\right)}{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)} \\ j=1,2, \cdots, n ; \quad l=1,2, \cdots, S_{j} ; \quad k=1,2, \cdots, K \end{array} P(X(j)=ajl∣Y=ck)=∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl,yi=ck)j=1,2,⋯,n;l=1,2,⋯,Sj;k=1,2,⋯,K
式中, x i ( j ) x_{i}^{(j)} xi(j) 是第 i 个样本的第 j 个特征; a j l a_{j l} ajl 是第 j 个特征可能取的第 l 个值; I I I 为指 display function.
边栏推荐
猜你喜欢
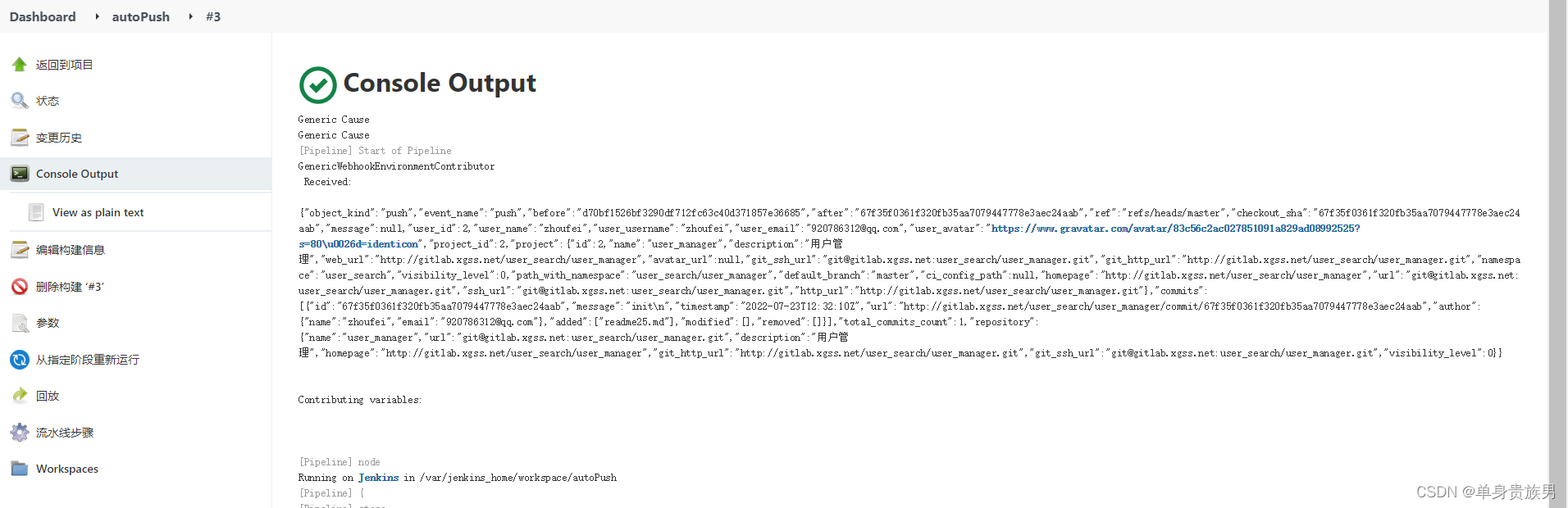
Jenkins--部署--3.1--代码提交自动触发jenkins--方式1

RestTemlate源码分析及工具类设计

自定义卡包效果实现
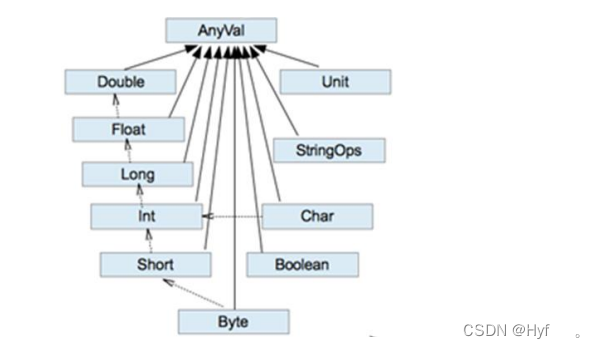
Scala类型转换
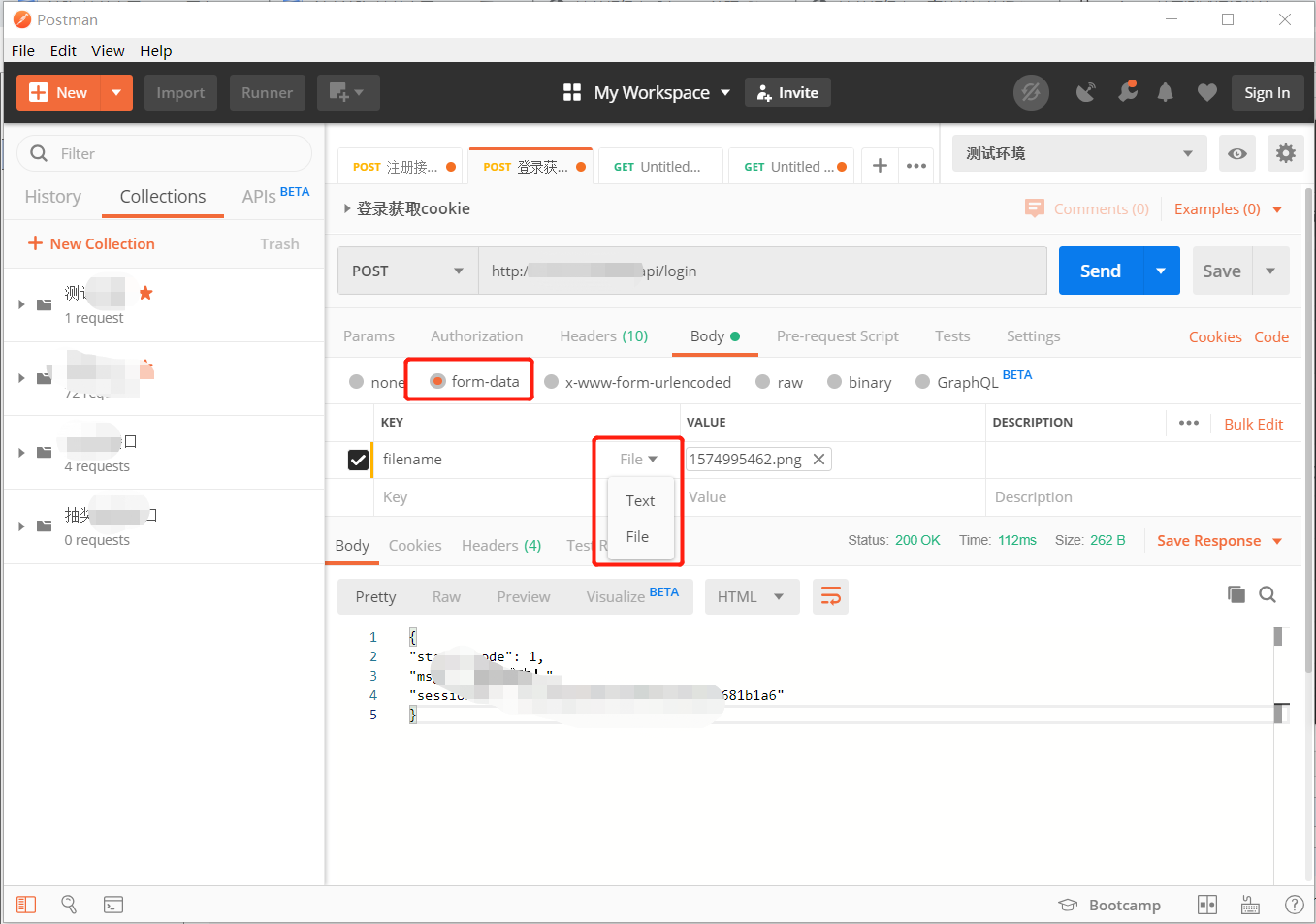
How to use postman

曲折的tensorflow安装过程(Tensorflow 安装问题的解决)
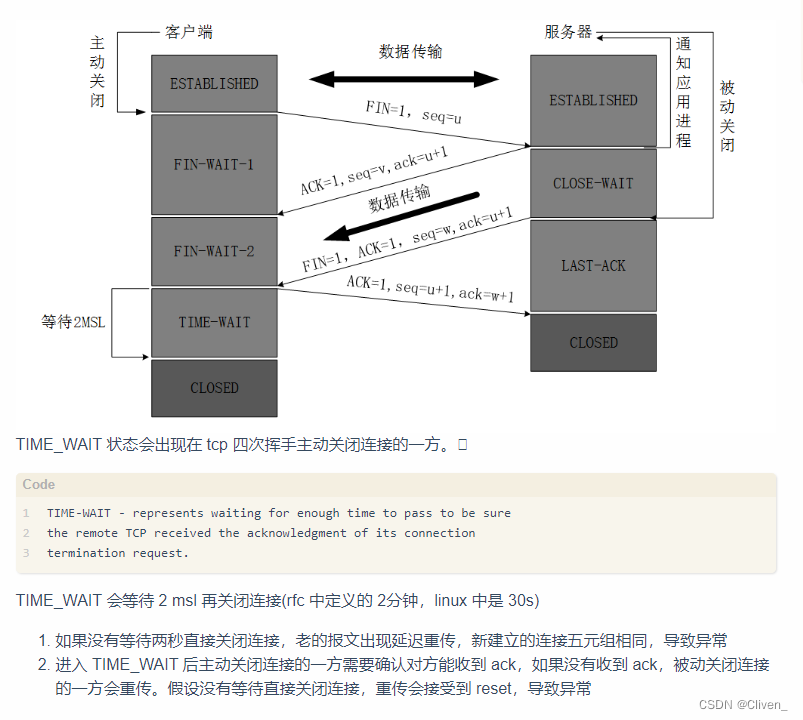
测试时大量TIME_WAIT

Spend 2 hours a day to make up for Tencent T8, play 688 pages of SSM framework and Redis, and successfully land on Meituan
干货|如何在海量文件系统中选择合适自己的文件系统

It's time for bank data people who are driven crazy by reporting requirements to give up using Excel for reporting
随机推荐
【微信小程序】本地服务页面案例实现
Jenkins--基础--6.1--Pipeline--介绍
李航《统计学习方法》笔记之朴素贝叶斯法
What is the function of the import command of the page directive in JSP?
稳定币:对冲基金做空 Tether 的结局会是什么?
uvm-phase机制
【Redis】Jedis
【微信小程序2】事件绑定
YugaByte adds Voyager migration service in its 2.15 database update
高效时代,电商运营如何靠RPA快速提效?
【Redis】通用命令
一文带你了解推荐系统常用模型及框架
MySQL安装与卸载详细教程
cococreator 动态设置精灵
大厂外包,值得拥有吗?
十、 网络管理
在全志V853开发板试编译QT测试
HikariCP数据库连接池,太快了!
初学者怎么快速学会SQL
RestTemlate源码分析及工具类设计