当前位置:网站首页>Reverse Polish notation
Reverse Polish notation
2022-07-05 13:02:00 【accumulate steadily ض】
The inverse Polish expression of stack application
What is the inverse Polish expression ??--> Source force buckle 150. Evaluate the inverse Polish expression
Reverse Polish notation :
The inverse Polish expression is a suffix expression , The so-called suffix means that the operator is written after .
The usual formula is a infix expression , Such as ( 1 + 2 ) * ( 3 + 4 ) .
The inverse Polish expression of the formula is written as ( ( 1 2 + ) ( 3 4 + ) * ) .
The inverse Polish expression has two main advantages :There is no ambiguity in the expression after removing the brackets , Even if the above formula is written as 1 2 + 3 4 + * You can also calculate the correct result according to the order .
It is suitable for stack operation : When it comes to numbers, it's on the stack ; When you encounter an operator, you take out two numbers at the top of the stack to calculate , And push the results into the stack
That is to say, we usually write correctly Addition, subtraction, multiplication and division of numbers , It's all like this .. For example : ( 1 + 2 ) * ( 3 + 4 )--> Infix expression , And we can make the computer understand ??-> This introduces today's inverse Polish expression, that is, the suffix expression , Let's turn infix expression into suffix expression .
for example :1+2*3+(4*2+5)*6

- Add curly braces to all operations
- Move the operator outside the corresponding bracket
- Remove all parentheses
Well, we get a suffix expression --> That is, the calculation that the computer can read
How does the computer calculate the result through such a suffix expression ???
That is our magical data structure --> Stack

- When encountering numbers, it will be added to the stack
- When you encounter an operator, you will get two numbers
- The first output is placed on the right side of the operator , The second time out is to the left of the release operator
- After the calculation, continue to put it on the stack
- The final stack top element is the result of the final expression calculation
Code implementation :
class Solution {
public int evalRPN(String[] tokens) {
// Ideas : When it comes to numbers, put them on the stack , If you encounter a number symbol, you will give two numbers to calculate
// Continue to stack the calculation results , Continue to traverse the end of the string
Stack<Integer> stack = new Stack<>();
for(int i =0;i<tokens.length;++i){
String str = tokens[i];
if(!isNumCharacter(str)){// Judge whether it is a symbol
// If it's a number, put it on the stack
int num = Integer.parseInt(str);
stack.push(num);
}else{
// If it's a character, pop the stack , Pop up two numbers
int num2 = stack.pop();
int num1 = stack.pop();
switch(str){
case "+":
stack.push(num1+num2);
break;
case "-":
stack.push(num1-num2);
break;
case "*":
stack.push(num1*num2);
break;
case "/":
stack.push(num1/num2);
break;
}
}
}
return stack.peek();
}
// Used to determine whether this string is a character
public boolean isNumCharacter(String s){
if(s.equals("+")||s.equals("*")||
s.equals("-")||s.equals("/")){
return true;
}
return false;
}
}边栏推荐
- leetcode:221. 最大正方形【dp状态转移的精髓】
- It's too convenient. You can complete the code release and approval by nailing it!
- A few years ago, I outsourced for four years. Qiu Zhao felt that life was like this
- 深度长文探讨Join运算的简化和提速
- What is the difference between Bi software in the domestic market
- mysql拆分字符串做条件查询
- How to protect user privacy without password authentication?
- HiEngine:可媲美本地的云原生内存数据库引擎
- 关于 SAP UI5 getSAPLogonLanguage is not a function 的错误消息以及 API 版本的讨论
- 谈谈我写作生涯的画图技巧
猜你喜欢
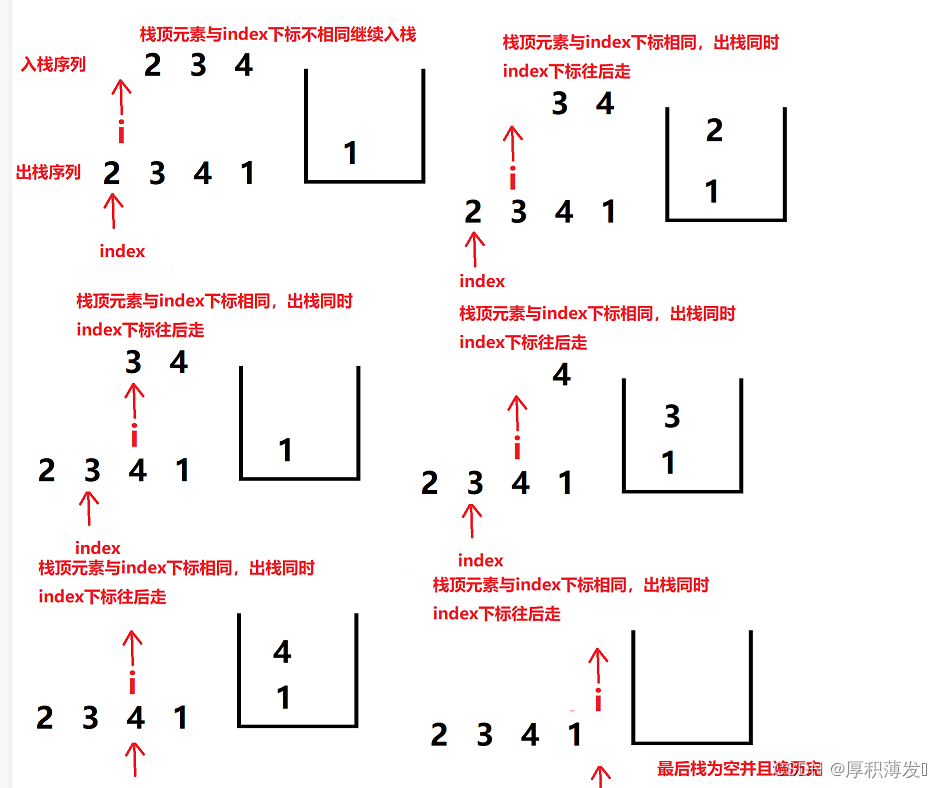
946. 验证栈序列
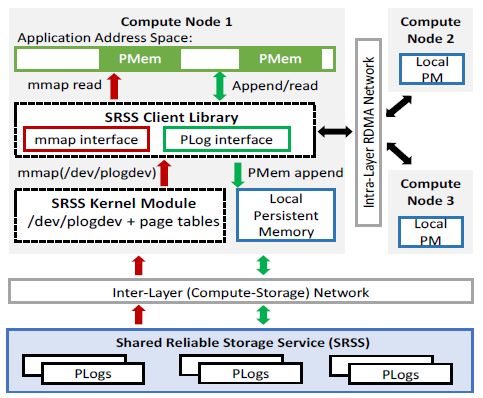
Hiengine: comparable to the local cloud native memory database engine

946. Verify stack sequence

Vonedao solves the problem of organizational development effectiveness
Comprehensive upgrade of Taobao short video photosynthetic platform
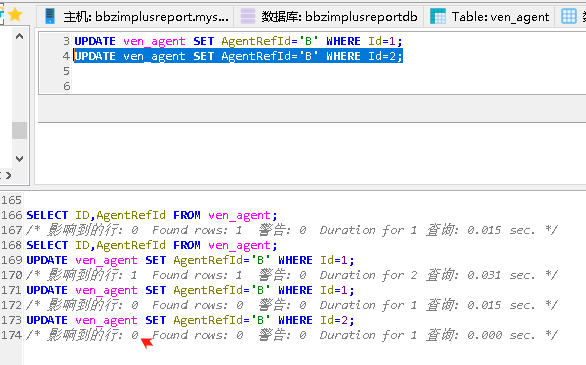
MySQL giant pit: update updates should be judged with caution by affecting the number of rows!!!
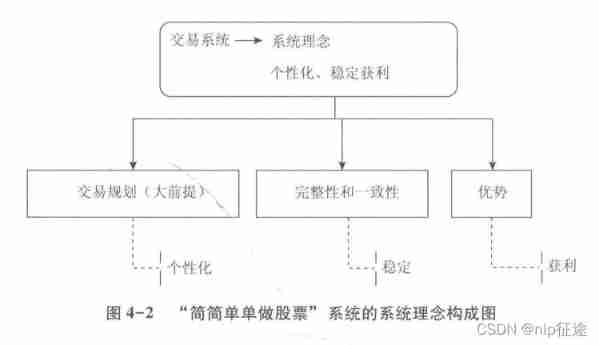
Simply take stock reading notes (4/8)
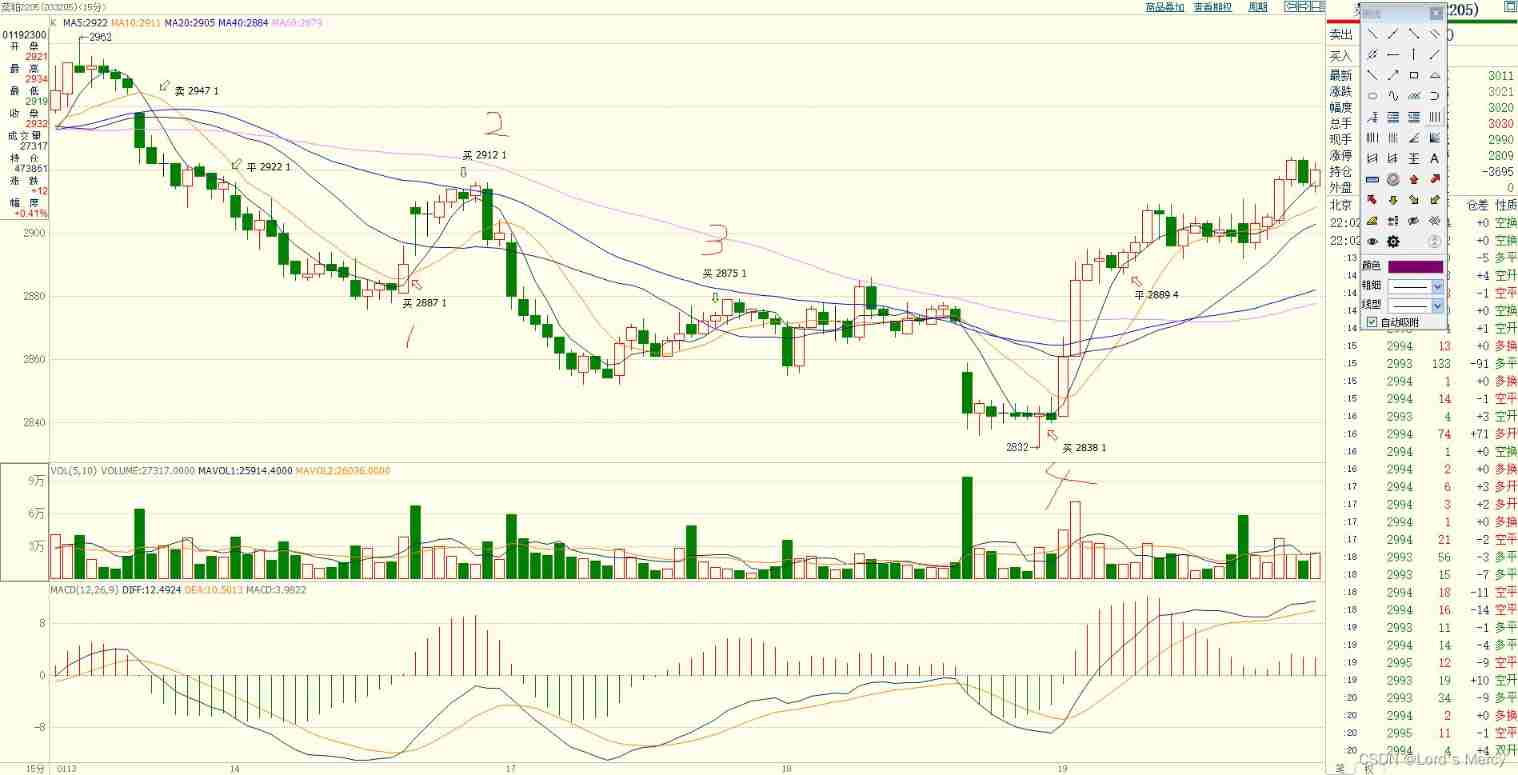
Transactions from January 14 to 19, 2022
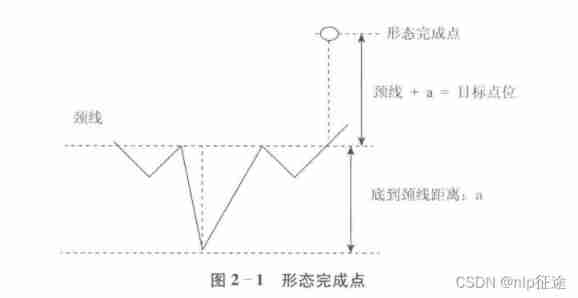
Simply take stock reading notes (2/8)
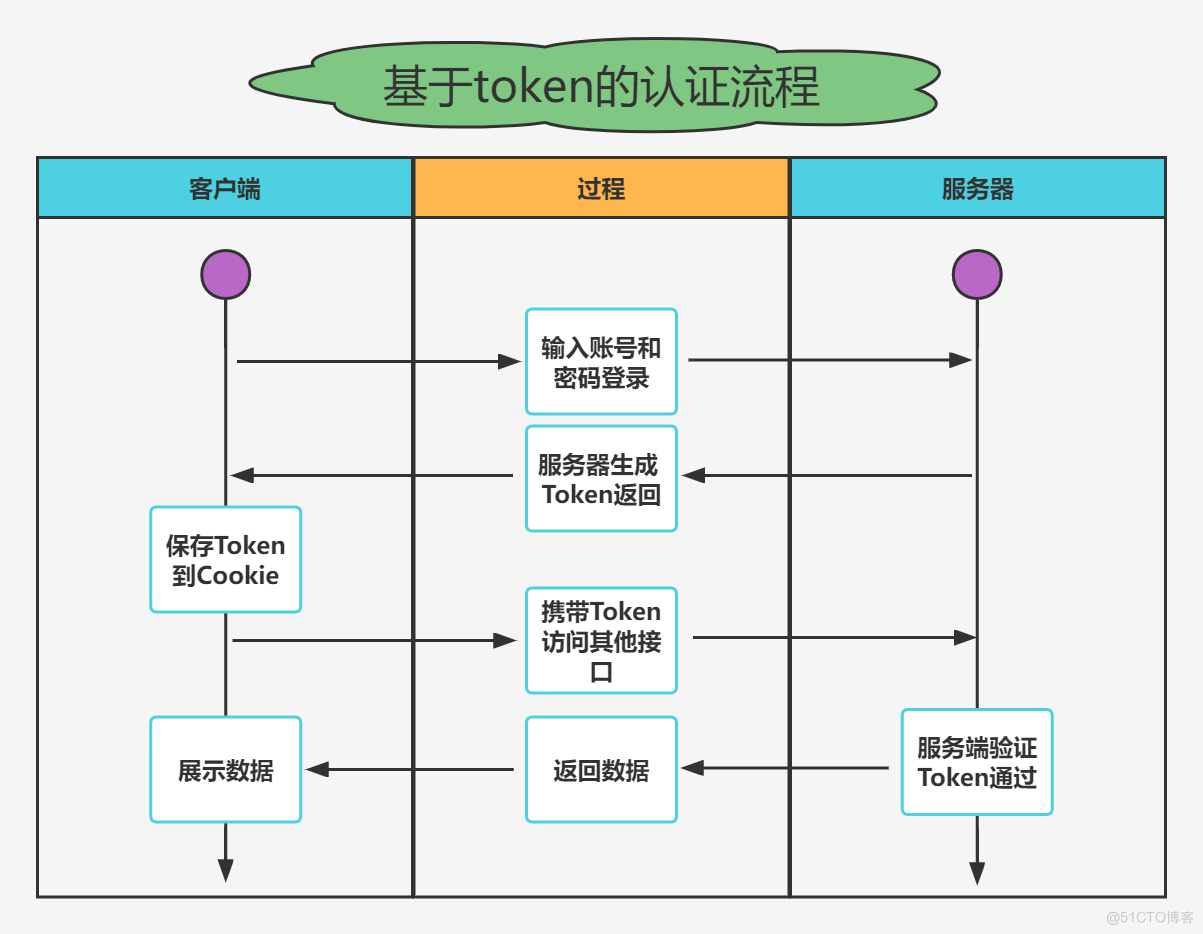
Actual combat simulation │ JWT login authentication
随机推荐
RHCSA2
155. 最小栈
解决 UnicodeDecodeError: ‘gbk‘ codec can‘t decode byte 0xa2 in position 107
RHCSA4
SAP ui5 objectpagelayout control usage sharing
Taobao flag insertion remarks | logistics delivery interface
[Nacos cloud native] the first step of reading the source code is to start Nacos locally
What if wechat is mistakenly sealed? Explain the underlying logic of wechat seal in detail
RHCSA1
Kotlin process control and circulation
Vonedao solves the problem of organizational development effectiveness
Transactions from January 14 to 19, 2022
Lepton 无损压缩原理及性能分析
Difference between JUnit theories and parameterized tests
解决uni-app配置页面、tabBar无效问题
I'm doing open source in Didi
Introduction to sap ui5 dynamicpage control
Alipay transfer system background or API interface to avoid pitfalls
Yyds dry goods inventory # solve the real problem of famous enterprises: move the round table
Principle and performance analysis of lepton lossless compression