【Day1】 deep-learning-basics

ps： I still think csdn Better than blog Garden . Write it down here .

get!New

1. yield keyword

1. contain yield The function of is called 【 Generator function 】, call 【 Generator function 】 The result returned is called 【 generator 】
2.【 generator 】 The object is actually 【 iterator 】, So it must be satisfied 【 iterator protocol 】：

• __iter__ Returns the iterator object itself
• __next__ One iteration at a time , If there is no data , Throw StopIteration abnormal

It works in the same way as the iterator ：

• adopt next() Function call
• Every time next() Will encounter yield Then return the result
• If the function ends （ That is to meet return） Throw out StopIteration abnormal

4.yield The most fundamental function of keywords is to change the nature of functions , Returns the object , Similar to class
5.yield sentence (Python2.2)：Simple Generators
6.yield expression (Python2.5)：Coroutines【 coroutines 】 via Enhanced Generators

#  This function has been saved in d2lzh The bag is convenient for later use 
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)  #  The reading order of samples is random 
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i: min(i + batch_size, num_examples)])
        yield features.take(j), labels.take(j)  # take Function returns the corresponding element according to the index 
       
batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break #  It's better to traverse it randomly 

2. Use autograd Automatic derivation

from mxnet import autograd

x.attach_grad() Apply for memory required to store gradients .
for example ： function $y=2{\mathbf{x}}^{\top }\mathbf{x}$ About $\mathbf{x}$ The gradient of should be $4\mathbf{x}$
First , Need to call autograd.record() requirement MXNet Record the calculations related to finding the gradient .
（ It can be done to 【 control flow （ Such as condition and cycle control ）】 Find gradient ）

with autograd.record():
    y = 2 * nd.dot(x.T, x)

then ,y.backward() Automatic gradient

Linear regression linear-regression

scratch

from mxnet import autograd, nd
import random

Training set $\mathbf{X}\in {\mathbb{R}}^{1000\times 2}$

sample 1000, The number of features 2

label $\mathbf{y}=\mathbf{X}\mathbf{w}+b+ϵ$

Real weight of linear regression model $\mathbf{w}=[2,-3.4{]}^{\top }$
deviation $b=4.2$
Random noise terms $ϵ$（ Noise term $ϵ$ To obey the mean is 0、 The standard deviation is 0.01 Is a normal distribution ）

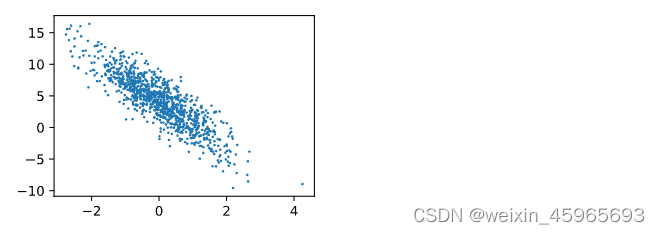
x:features y:labels

initialization 【 Model parameters 】： The weight is initialized to mean 0、 The standard deviation is 0.01 The normal random number of , The deviation is initialized to 0
Definition 【 Loss function 】： Loss of square
Definition 【 optimization algorithm 】： Small batch random gradient descent algorithm
Training models ： In each iteration , According to the small batch of data samples currently read （ features X And labels y）, By calling The inverse function backward Calculate small batch random gradient And call 【 optimization algorithm 】sgd iteration 【 Model parameters 】 To optimize 【 Loss function 】.

# Initialize model parameters 
w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))
params = [w, b]
for param in params:
	param.attach_grad()
# Defining models 
def net(X):
	return nd.dot(X, w) + b
# Loss function 
def squared_loss(y_hat, y):  #  This function has been saved in d2lzh The bag is convenient for later use 
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
# Optimize  
def sgd(params, lr, batch_size):  #  This function has been saved in d2lzh The bag is convenient for later use 
    for param in params:
        param[:] = param - lr * param.grad / batch_size
        
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):  #  The training model requires a total of num_epochs Iterations 
    #  In each iteration cycle , All samples in the training dataset will be used once （ Suppose the number of samples can be divided by the batch size ）.X
    #  and y They are the characteristics and labels of small batch samples 
    for X, y in data_iter(batch_size, features, labels):
        with autograd.record():
            l = loss(net(X, w, b), y)  # l It's about small batches X and y The loss of 
        l.backward()  #  The loss of small batch has a gradient on the model parameters 
        sgd([w, b], lr, batch_size)  #  Small batch stochastic gradient descent iterative model parameters are used 
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))

gluon

from mxnet.gluon import nn
net = nn.Sequential()
net.add(nn.Dense(1))

from mxnet import init
net.initialize(init.Normal(sigma=0.01))

from mxnet.gluon import loss as gloss
loss = gloss.L2Loss()  #  The square loss is also called L2 Norm loss 

from mxnet import gluon
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.03})

num_epochs = 3
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        with autograd.record():
            l = loss(net(X), y)
        l.backward()
        trainer.step(batch_size)
    l = loss(net(features), labels)
    print('epoch %d, loss: %f' % (epoch, l.mean().asnumpy()))

Multiple logistic regression softmax-regression

scratch

problem 1. exp It will lead to poor numerical stability
https://freemind.pluskid.org/machine-learning/softmax-vs-softmax-loss-numerical-stability/

def softmax(X):
    X_exp = X.exp()#  Become positive 
    partition = X_exp.sum(axis=1, keepdims=True)#  Sum up the lines 
    return X_exp / partition  #  The broadcast mechanism is applied here 
    #  bring , Every line is a positive sum 1

def net(X):
	return softmax(nd.dot(X.reshape((-1,num_inputs)), W) + b)

【 Cross entropy loss function 】： Take the negative cross entropy of the two probability distributions as the target value
Minimizing this value is equivalent to maximizing the similarity of these two probabilities

【 Calculation accuracy 】： The class with the highest prediction probability is regarded as the prediction class , Calculate by comparing the real label

def cross_entropy(yhat, y):
	return - nd.pick(nd.log(yhat),y)

def accuracy(output, label):
	return nd.mean(output.argmax(axis=1)==label).asscalar()

#  This function has been saved in d2lzh The bag is convenient for later use . The function will be improved step by step ： Its full implementation will be in “ Image enlargement ” In a section 
#  describe 
def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        y = y.astype('float32')
        acc_sum += accuracy(net(X),y)
        n += y.size
    return acc_sum / n

Training +accuracy test_acc

num_epochs, lr = 5, 0.1

#  This function has been saved in d2lzh The bag is convenient for later use 
def train_ch3(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, trainer=None):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum()
            l.backward()
            if trainer is None:
                d2l.sgd(params, lr, batch_size)
            else:
                trainer.step(batch_size)  # “softmax The simple realization of return ” I'm going to use 
            y = y.astype('float32')
            train_l_sum += l.asscalar()
            train_acc_sum += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n += y.size
        test_acc = evaluate_accuracy(test_iter, net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'
              % (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, batch_size,
          [W, b], lr)

gluon

net = nn.Sequential()
with net.name_scope():
	net.add(gluon.nn.Flatten())#  Input 
	net.add(nn.Dense(10))#  Output 
net.initialize(init.Normal(sigma=0.01))
# Softmax Together with cross entropy 
softmax_cross_entropy = gluon.loss.SoftmaxCrossEntropyLoss()
#  Use learning rate is 0.1 The small batch random gradient descent is used as the optimization algorithm 
trainer = gluon.Trainer(net.collect_params(), 'sgd', {
    'learning_rate': 0.1})

Multilayer perceptron

Scratch

Activation function ： Insert between layers 【 nonlinear 】 The activation function of $relu(x)=max(x,0)$（ Simple calculation ）

def relu(X):
	return nd.maximum(X, 0)

def net(X):
    X = X.reshape((-1, num_inputs))
    H = relu(nd.dot(X, W1) + b1)
    return nd.dot(H, W2) + b2

gluon

net = nn.Sequential()
with net.name_scope():
	net.add(nn.Flatten())
	net.add(nn.Dense(256, activation='relu'),nn.Dense(10))
	#  Add a few more hidden layers 
	net.add(nn.Dense(256, activation='relu'),nn.Dense(10))
	net.add(nn.Dense(10))
net.initialize(init.Normal(sigma=0.01))

Under fitting and over fitting underfit-overfit

Under fitting ： The training error is very large
Over fitting ： Training error The generalization error The difference is too large

Polynomial fitting
$$\hat{y}=b+\sum _{k=1}^K{x}^k{w}_k$$

The goal is ： Find one. K Order polynomial , It consists of vectors $w$ And displacement $b$ form , To best approximate each sample $x$ and $y$, And take the square error as the loss function .
Specially , First order polynomial fitting is also called linear fitting .

Specifically generate data samples
$$y=1.2x-3.4x^2+5.6x^3+5.0+noise$$

n_train, n_test, true_w, true_b = 100, 100, [1.2, -3.4, 5.6], 5
features = nd.random.normal(shape=(n_train + n_test, 1))
poly_features = nd.concat(features, nd.power(features, 2),
                          nd.power(features, 3))
labels = (true_w[0] * poly_features[:, 0] + true_w[1] * poly_features[:, 1]
          + true_w[2] * poly_features[:, 2] + true_b)
labels += nd.random.normal(scale=0.1, shape=labels.shape)

A little

def fit_and_plot(train_features, test_features, train_labels, test_labels)

Third order polynomial fitting

fit_and_plot(poly_features[:n_train, :], poly_features[n_train:, :],
             labels[:n_train], labels[n_train:])

Linear fitting

fit_and_plot(features[:n_train, :], features[n_train:, :], labels[:n_train],
             labels[n_train:])

The training sample is insufficient

fit_and_plot(poly_features[0:2, :], poly_features[n_train:, :], labels[0:2],
             labels[n_train:])

Regularization reg【 penalty 】

introduce ${\mathbf{L}}_2$ Norm regularization
Our minimization during training becomes ：
$$loss+\lambda \sum _{p\in params}||p|{|}_2^2$$

1.fit loss 2. The trade-off model should not be particularly complex . Intuitively ,${\mathbf{L}}_2$ Try to punish parameter values with larger absolute values , bring $w$ and $b$ Make it smaller .
It is worth noting that , When testing the model ,$\lambda$ It has to be for 0.

def net(X, lambd, w, b):
	return nd.dot(X, w) + b + lambd * ((w**2).sum() + b**2)

Using high-dimensional linear regression, we introduce a 【 Over fitting 】 problem
Use the following linear function to generate data samples
$$y=0.05+\sum _{i=1}^{p}0.01x_i+noise$$